LLaMA中ROPE位置编码实现源码解析
1、Attention中q,经下式,生成新的q。m为句长length,d为embedding_dim/head
θ i = 1 1000 0 2 i d \theta_i=\frac{1}{10000^\frac{2i}{d}} θi=10000d2i1
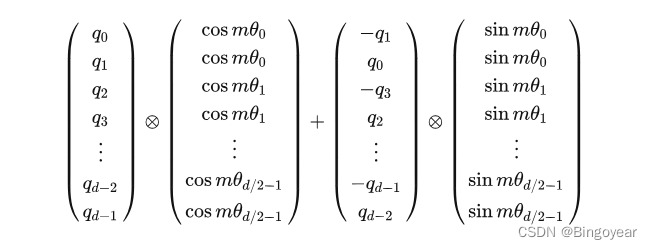
2、LLaMA中RoPE源码
import torchdef precompute_freqs_cis(dim: int, end: int, constant: float = 10000.0):'''计算cos和sin的值,cos值在实部,sin值在虚部,类似于 cosx+j*sinx:param dim: q,k,v的最后一维,一般为emb_dim/head_num:param end: 句长length:param constant: 这里指10000:return:复数计算 torch.polar(a, t)输出, a*(cos(t)+j*sin(t))'''# freqs: 计算 1/(10000^(2i/d) ),将结果作为参数theta# 形式化为 [theta_0, theta_1, ..., theta_(d/2-1)]freqs = 1.0 / (constant ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim)) # [d/2]# 计算mt = torch.arange(end, device=freqs.device) # [length]# 计算m*thetafreqs = torch.outer(t, freqs).float() # [length, d]# freqs形式化为 [m*theta_0, m*theta_1, ..., m*theta_(d/2-1)],其中 m=0,1,...,length-1# 计算cos(m*theta)+j*sin(m*theta)freqs_cis = torch.polar(torch.ones_like(freqs), freqs) # complex64# freqs_cis: [cos(m*theta_0)+j*sin(m*theta_0), cos(m*theta_1)+j*sin(m*theta_1),), ..., cos(m*theta_(d/2-1))+j*sin(m*theta_(d/2-1))]# 其中j为虚数单位, m=0,1,...,length-1return freqs_cis # [length, d]def reshape_for_broadcast(freqs_cis: torch.Tensor, x: torch.Tensor):ndim = x.ndimassert 0 <= 1 < ndimassert freqs_cis.shape == (x.shape[1], x.shape[-1])shape = [d if i == 1 or i == ndim - 1 else 1 for i, d in enumerate(x.shape)] # (1, length, 1, d/2)return freqs_cis.view(*shape) # [1, length, 1, d/2]def apply_rotary_emb(xq: torch.Tensor, xk: torch.Tensor, freqs_cis: torch.Tensor,):# 先将xq维度变为[bs, length, head, d/2, 2], 利用torch.view_as_complex转变为复数# xq:[q0, q1, .., q(d-1)] 转变为 xq_: [q0+j*q1, q2+j*q3, ..., q(d-2)+j*q(d-1)]xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2)) # [bs, length, head, d/2]# 同样的,xk_:[k0+j*k1, k2+j*k3, ..., k(d-2)+j*k(d-1)]xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))freqs_cis = reshape_for_broadcast(freqs_cis, xq_) # [1, length, 1, d/2]# 下式xq_ * freqs_cis形式化输出,以第一个为例, 如下# (q0+j*q1)(cos(m*theta_0)+j*sin(m*theta_0)) = q0*cos(m*theta_0)-q1*sin(m*theta_0) + j*(q1*cos(m*theta_0)+q0*sin(m*theta_0))# 上式的实部为q0*cos(m*theta_0)-q1*sin(m*theta_0),虚部为q1*cos(m*theta_0)+q0*sin(m*theta_0)# 然后通过torch.view_as_real函数,取出实部和虚部,维度由[bs, length, head, d/2]变为[bs, length, head, d/2, 2],最后一维放实部与虚部# 最后经flatten函数将维度拉平,即[bs, length, head, d]# 此时xq_out形式化为 [实部0,虚部0,实部1,虚部1,..., 实部(d/2-1), 虚部(d/2-1)]xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(3) # [bs, length, head, d]# 即为新生成的qxk_out = torch.view_as_real(xk_ * freqs_cis).flatten(3)return xq_out.type_as(xq), xk_out.type_as(xk)if __name__=='__main__':# (bs, length, head, d)q = torch.randn((2, 10, 12, 32)) # q=[q0, q1, .., qd-1]k = torch.randn((2, 10, 12, 32))v = torch.randn((2, 10, 12, 32))freqs_cis= precompute_freqs_cis(dim=32, end=10, constant= 10000.0)# print(freqs_cis.detach().numpy())q_new, k_new = apply_rotary_emb(xq=q, xk=k, freqs_cis=freqs_cis)print()3、表示
看1中的公式表示,q0和q1相互作用,得到新的q0和q1,也即
q 0 n e w = q 0 ∗ c o s ( m θ 0 ) − q 1 ∗ s i n ( m θ 0 ) q^{new}_0=q_0*cos(m\theta_0)-q_1*sin(m\theta_0) q0new=q0∗cos(mθ0)−q1∗sin(mθ0)
q 1 n e w = q 1 ∗ c o s ( m θ 0 ) + q 0 ∗ s i n ( m θ 0 ) q^{new}_1=q_1*cos(m\theta_0)+q_0*sin(m\theta_0) q1new=q1∗cos(mθ0)+q0∗sin(mθ0)
这里将 ( q 0 , q 1 ) (q_0,q_1) (q0,q1)、 ( q 0 n e w , q 1 n e w ) (q^{new}_0,q^{new}_1) (q0new,q1new)看做向量,很明显上式是向量旋转,旋转角度为逆时针 m θ 0 m\theta_0 mθ0
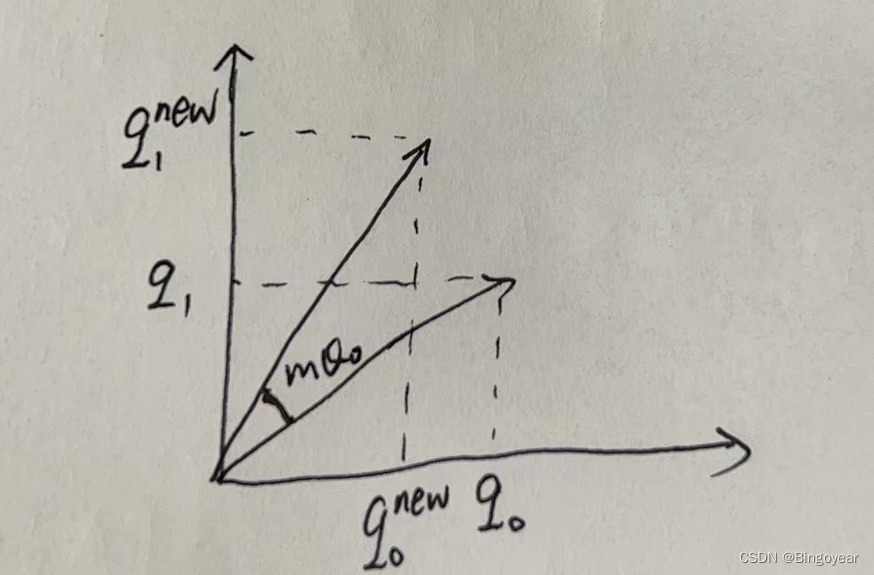
可与PalM中ROPE实现方式做对比
PaLM中ROPE位置编码实现源码解析
