线性代数的学习和整理4: 求逆矩阵的多种方法汇总
目录
原始问题:如何求逆矩阵?
1 EXCEL里,直接可以用黑盒表内公式 minverse() 数组公式求A-
2 非线性代数方法:解方程组的方法
3 增广矩阵的方法
4 用行列式的方法计算(未验证)
5 A-=1/|A|*A* (未验证)
原始问题:如何求逆矩阵?
求逆矩阵的方法很多
- 方法1:矩形计算展开为方程组,解方程组得出A-的各个元素
- 方法2:利用增广矩阵,进行线性变换来求A-
- 方法3:行列数的方法
- 方法4
1 EXCEL里,直接可以用黑盒表内公式 minverse() 数组公式求A-
- 除了各种手动计算的方法,EXCEL可以使用 minverse() 函数计算逆矩阵
- 只要提前选好多个单元格,输入数组公式miniverse()即可,结果是没问题
- 错误点:选中的单元格范围不对,没有按shift+ctrl+enter 三键输入数组公式

2 非线性代数方法:解方程组的方法
这种方法理论上纯粹用函数方程组即可
- 设置逆矩阵的内部数据分别为变量x1,x2....
- 利用利用 A*A- =I, 也就是这2个矩阵相乘*逆矩阵=I
- 形成的方程组解方程求出x1,x2....
- 从而就可以计算出 逆矩阵

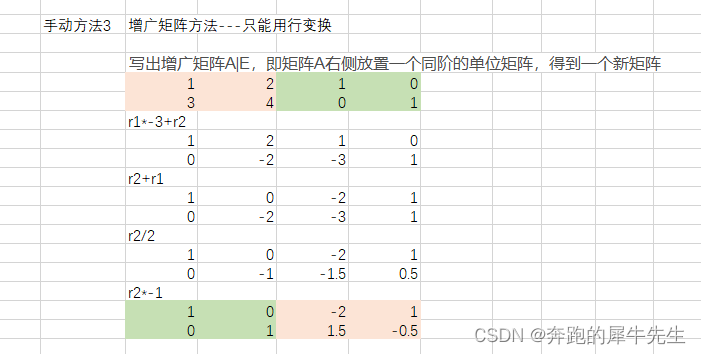
3 增广矩阵的方法
- 使用增广矩阵变幻时,只能用行变换,不能用列变换。因为如果用列变换,会影响 I的列和矩阵的列的混乱
- 使用增广矩阵进行行变换,让A*I=I*A- 即可求出逆矩阵A-
4 用行列式的方法计算(未验证)
这个方法不是我的,来源
用这个方法求逆矩阵:稳如狗让一切繁琐问题都有其猥琐解法https://mp.weixin.qq.com/s?__biz=MzIxMDM0Mjg1Mw==&mid=2247483954&idx=1&sn=27f233069f43f8c0ce3d4e6c135a0de8&chksm=97674498a010cd8e0cb7e6285f3fd51d76e4113f80d5cc00a5888cb405efd07bd153611ba97b&scene=27


5 A-=1/|A|*A* (未验证)

