手撕 `np.transpose` : 三维数组的循环转置
手撕 np.transpose : 三维数组的循环转置
手撕 np.transpose 2D
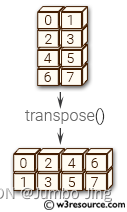
- 何为transpose ?
如上图: 二维的例子, 直观地理解就是沿着对角线拉平(对角关系左上右下依旧), 其他位置依次填充.
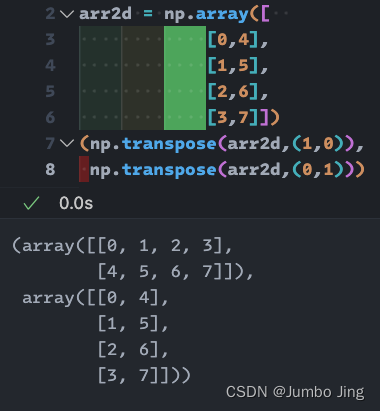
2. 2D数组中0,1 为原始参, 1,0 为转置参
- 原始参即数组的原始形态: 比如👆🏻shape为(4,2), 调用元参 即复原原始状态, 即使数组转置本身(自转)也是一样.
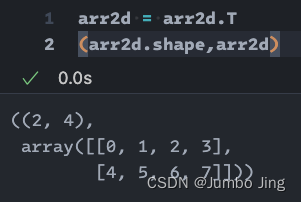
- 转置参为转置形态: 👆🏻shape为(2,4), 调用转参 即进入转置状态, 当数组转置本身时, 数组会在(2,4)和(4,2)互相转换. 在2D矩阵中和.T相同 👇
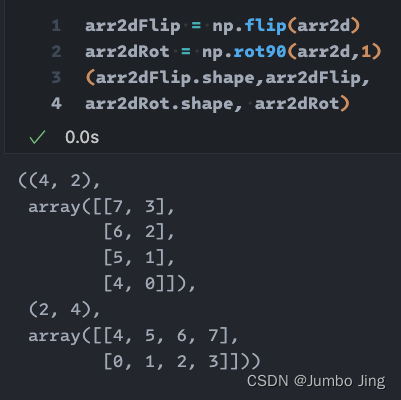
3. np.flip 和 np.rot90
- rot90 : 逆时针躺平(
k=1) - flip 翻转: 👇🏻shape不变, 翻转180°, 相当于连续
rot902次
手撕3D转置:
- 源阵:
arr = np.array([[[11,12,13,14], [21,22,23,24], [31,32,33,34]],[[41,42,43,44], [51,52,53,54], [61,62,63,64]]])
(arr.shape, arr)大-中-小(zyx)
((2, 3, 4),array([[[11, 12, 13, 14],[21, 22, 23, 24],[31, 32, 33, 34]],[[41, 42, 43, 44],[51, 52, 53, 54],[61, 62, 63, 64]]]))参数2, 轴 (0,1,2)
撕! 撕! 撕!
公转
012–zyx- shape: 大-中-小
arr012 = np.transpose(arr,(0,1,2))
(arr012.shape, arr012)((2, 3, 4),array([[[11, 12, 13, 14],[21, 22, 23, 24],[31, 32, 33, 34]],[[41, 42, 43, 44],[51, 52, 53, 54],[61, 62, 63, 64]]]))
021–zxy- shape: 大-小-中
...
((2, 4, 3),array([[[11, 21, 31],[12, 22, 32],[13, 23, 33],[14, 24, 34]],[[41, 51, 61],[42, 52, 62],[43, 53, 63],[44, 54, 64]]]))
120–yzx- shape: 中-大-小
...
((3, 4, 2),array([[[11, 41],[12, 42],[13, 43],[14, 44]],[[21, 51],[22, 52],[23, 53],[24, 54]],[[31, 61],[32, 62],[33, 63],[34, 64]]]))
102–yxz- shape: 中-小-大
...
((3, 2, 4),array([[[11, 12, 13, 14],[41, 42, 43, 44]],[[21, 22, 23, 24],[51, 52, 53, 54]],[[31, 32, 33, 34],[61, 62, 63, 64]]]))
201–xzy- shape: 小-大-中
((4, 2, 3),array([[[11, 21, 31],[41, 51, 61]],[[12, 22, 32],[42, 52, 62]],[[13, 23, 33],[43, 53, 63]],[[14, 24, 34],[44, 54, 64]]]))
210–xyz- shape: 小-中-大
((4, 3, 2),array([[[11, 41],[21, 51],[31, 61]],[[12, 42],[22, 52],[32, 62]],[[13, 43],[23, 53],[33, 63]],[[14, 44],[24, 54],[34, 64]]]))
自转
- 数组转置自身时变化:
arr012 = np.transpose(arr012,(0,1,2))
(arr012.shape, arr012)
...
元 参: 012 <-------一阶转参: 021 <–> 012一阶转参: 102 <–> 012一阶转参: 210 <–> 012二阶转参: 120 --> 201 --> 012 --> 120 …二阶转参: 201 --> 120 --> 012 --> 201 …
结论:
-
3D转置 在本例中,
元参为012用于还原原始结构, 一阶转参有3个, 在数组转置自身, 会和元参互相转换,相当于.T(瞎猜的) -
重点来了, 3D矩阵有2个二阶
转参很有意思, 在数组转置自身时, 这2个参数会和元参一起构成闭环形成三种转置状态无限循环.- 注意⚠️: 顺序是先找到另一个
转参, 在通过元参, 找回自身.
- 注意⚠️: 顺序是先找到另一个
-
3D转置 本身很抽象, 通过本次手撕实验观察到以下结果:
- 对角铁律: 在大阵中, 第一个元素和最后一个元素永远是第一个元素和最后一个元素
- 相邻铁律: 在中阵中,第一个元素和最后一个元素相邻关系不变
- 相差铁律: 在小阵中, 元素之间的index差值在同一维度永远为1
- 💡: 本文好几个名词是我自己杜xia撰bian的, 本文是被3D转置搞得头疼又停不下来逼出来的别太当真…
具体意义, 留待下文分解
<<未完待续>>
