题目

用队列实现栈

题目要求

题目链接

示例

解答

方法一、

使用两个队列来实现栈。

实现思路

题目说了使用两个队列来实现栈的操作，我们知道栈结构的特点是元素后进先出，而队列的特点是先进先出。即栈的操作是尾插尾删，而队列的操作是尾插头删，所以我们可以将一个队列中按顺序将数据入队来模仿元素进栈。

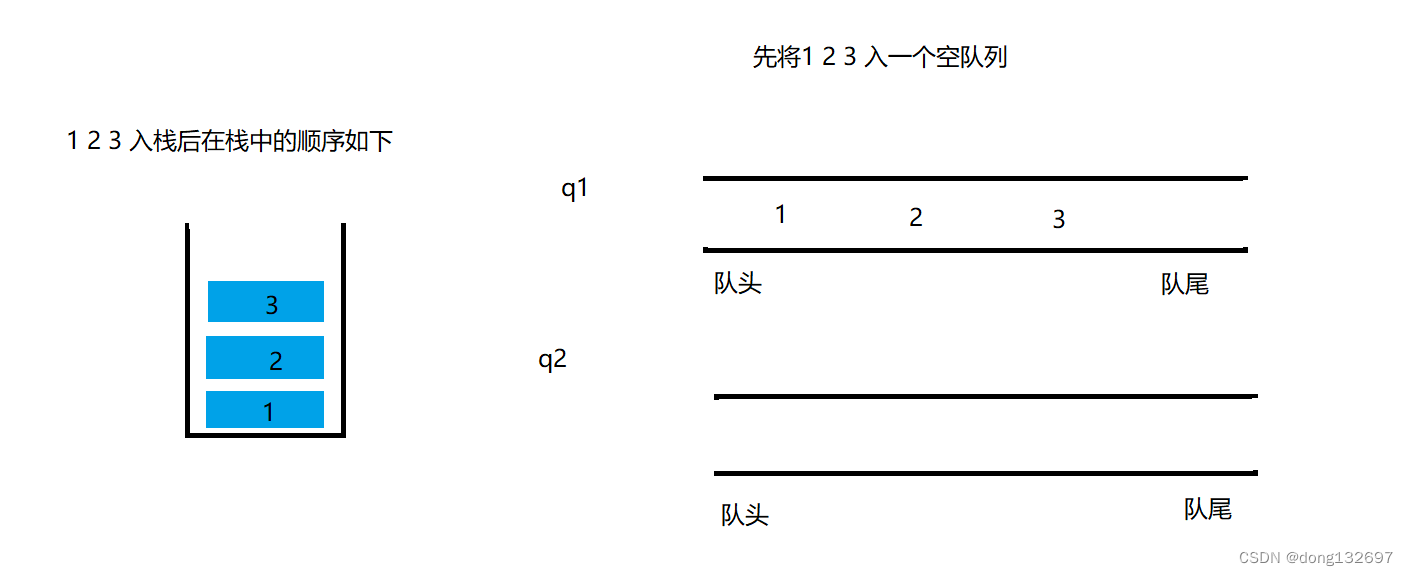
当元素出栈时，我们可以将有元素的队列q1的数据依次出队，并且依次进入到另一个空的队列q2，当队列q1中只有一个元素时，我们停止将这个元素入队q2，因为这个元素就相当于栈顶元素。

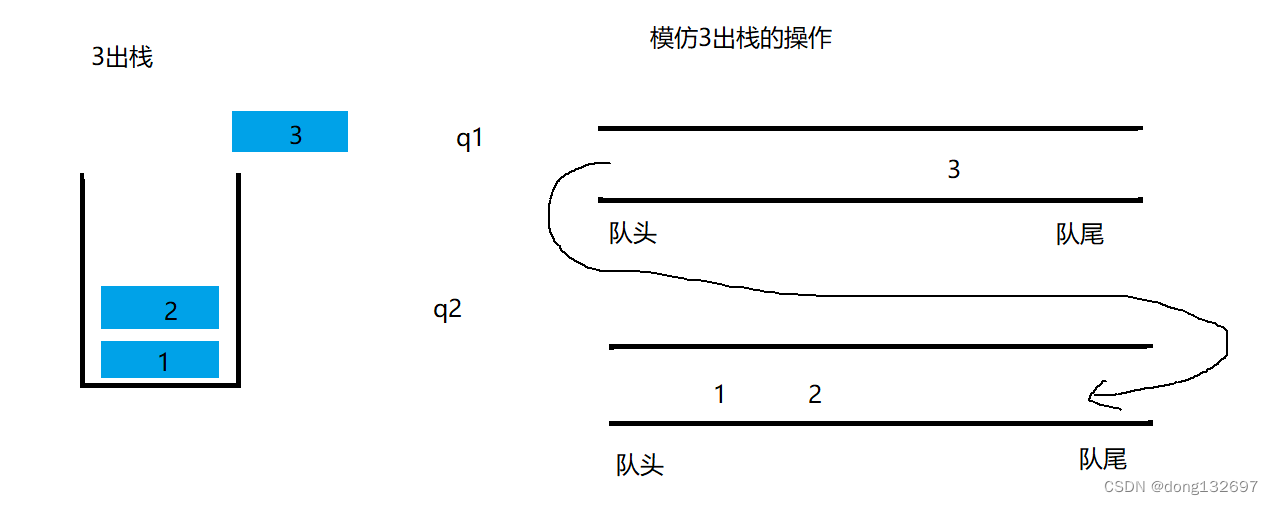
此时我们将这个元素的空间释放即完成了栈中元素的出栈操作，并且此时队列q1也为空队列了，当有元素需要入栈时，将元素进入到不是空队列的队列中即可，当再需要出栈时，还重复上面的操作，将队列中的元素都进入到另一个队列，然后将最后一个结点释放即可。

时间复杂度和空间复杂度

时间复杂度：出栈为O(N)，其余为O(1)
空间复杂度：O(N)

代码

include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>typedef int QDataType;
//队列的结点设计
typedef struct QueueNode
{struct QueueNode* next;QDataType data;
}QNode;//创建一个Queue结构体变量，就相当于创建了一个队列，该结构体变量中存的有该队列的头结点地址，尾结点地址
//所以当有该结构体变量的地址时，可以通过该地址改变队列的头结点地址和尾结点地址，即改变head指针和tail指针。
typedef struct Queue
{QNode* head;QNode* tail;int size;  //用来记录队列长度
}Queue;//队列初始化
void QueueInit(Queue* pq);//判断队列是否为空
bool QueueEmpty(Queue* pq);//队列的销毁
void QueueDestroy(Queue* pq);//元素的入栈
void QueuePush(Queue* pq, QDataType x);//元素的出栈
void QueuePop(Queue* pq);//返回队头结点的数据
QDataType QueueFront(Queue* pq);//返回队尾结点的数据
QDataType QueueBack(Queue* pq);//返回队列的长度
int QueueSize(Queue* pq);void QueueInit(Queue* pq)
{assert(pq);pq->head = NULL;pq->tail = NULL;
}bool QueueEmpty(Queue* pq)
{assert(pq);/*if (pq->head == NULL){return true;}else{return false;}*/return pq->head == NULL;
}void QueuePush(Queue* pq, QDataType x)
{assert(pq);QNode* newNode = (QNode*)malloc(sizeof(QNode));if (newNode == NULL){perror("malloc fail");exit(-1);}newNode->data = x;newNode->next = NULL;if (pq->head == NULL){pq->head = newNode;pq->tail = newNode;}else{pq->tail->next = newNode;pq->tail = newNode;}
}void QueuePop(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));//当队列中只有一个结点时，该结点出队后队列就为空了//所以需要将队列的头指针和尾指针都置为NULLif (pq->head->next == NULL){free(pq->head);pq->head = NULL;//虽然按照下面的处理pq->head也会为NULL，//但tail指针还指向已经释放空间的最后一个结点的地址，所以此时tail为野指针，所以需要特别处理，将tail置为NULLpq->tail = NULL;}else{QNode* del = pq->head;pq->head = pq->head->next;free(del);}}QDataType QueueFront(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->head->data;
}QDataType QueueBack(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->tail->data;
}int QueueSize(Queue* pq)
{assert(pq);int size = 0;QNode* curr = pq->head;while (curr != NULL){size++;curr = curr->next;}return size;
}void QueueDestroy(Queue* pq)
{assert(pq);QNode* curr = pq->head;while (curr){QNode* next = curr->next;free(curr);curr = next;}pq->head = NULL;pq->tail = NULL;//在这里面将pq置为空没用，因为pq只是临时创建的一个Queue*类型的结构体指针//pq里面存的是Queue结构体变量的地址，在函数里面将pq置为NULL对外面没有影响。//只是让pq指向不了这个结构体变量了，但是这个结构体变量还存在，
}//该结构体采用了匿名结构体，然后将这个匿名结构体重命名为MyStack
typedef struct {//创建两个队列Queue q1;Queue q2;
} MyStack;
bool myStackEmpty(MyStack* obj);MyStack* myStackCreate() {//此时MyStack就相当于一个栈，当我们要使用一个栈时，先申请空间创建一个MyStack的结点MyStack* stack = (MyStack*)malloc(sizeof(MyStack));//然后我们初始化两个队列，因为我们定义的QueueInit函数的形参为Queue*类型的指针，//而MyStack结构体中定义的成员变量q1和q2为Queue类型，所以要将q1和q2的地址传过去。//如果传的是stack->q1的话，那么函数会临时创建一个Queue类型的变量tmp，然后函数里面tmp改变//但是stack结构体里面的q1不会改变。QueueInit(&(stack->q1));QueueInit(&(stack->q2));return stack;
}void myStackPush(MyStack* obj, int x) {assert(obj);//先设q1为空队列，q2为非空队列Queue* emptyQ = &(obj->q1);Queue* noemptyQ = &(obj->q2);//如果q1非空，说明设错了，则改正。if(!QueueEmpty(&(obj->q1))){emptyQ = &(obj->q2);noemptyQ = &(obj->q1);}QueuePush(noemptyQ,x);
}int myStackPop(MyStack* obj) {//先判断栈是否为空，如果为空则不可以出栈assert(obj);assert(!myStackEmpty(obj));//先设q1为空队列，q2为非空队列Queue* emptyQ = &(obj->q1);Queue* noemptyQ = &(obj->q2);//如果q1非空，说明设错了，则改正。if(!QueueEmpty(&(obj->q1))){emptyQ = &(obj->q2);noemptyQ = &(obj->q1);}//将非空队列的除了最后一个元素外的元素都进入到空队列中，while(QueueSize(noemptyQ)>1){QueuePush(emptyQ,QueueFront(noemptyQ));QueuePop(noemptyQ);}//将非空队列中最后一个元素返回int top = QueueFront(noemptyQ);//将队列中最后一个元素出队。此时非空队列变为空队列QueuePop(noemptyQ);//返回栈顶元素的数据return top;
}int myStackTop(MyStack* obj) {assert(obj);//返回栈顶元素就相当于返回非空队列的队尾结点的元素。//判断栈非空assert(!myStackEmpty(obj));if(!QueueEmpty(&(obj->q1))){return QueueBack(&(obj->q1));}else{return QueueBack(&(obj->q2));}
}bool myStackEmpty(MyStack* obj) {assert(obj);//判断栈空就是判断两个队列是否都为空return QueueEmpty(&(obj->q1))&&QueueEmpty(&(obj->q2));
}void myStackFree(MyStack* obj) {assert(obj);//先释放两个队列的空间，然后再释放obj的空间QueueDestroy(&(obj->q1));QueueDestroy(&(obj->q2));free(obj);
}

方法二、

使用两个队列来实现栈。

实现思路

第一种方法是入栈的元素直接入队，当出栈时才进行转换，将栈顶元素出栈。而这个方法是在入栈时就将队列中的元素排好出栈的顺序。
当元素入栈时，将元素进入一个空队列中，然后将另一个非空队列noempty的元素都进入空队列empty中，这样空队列empty中元素的出队顺序刚好和在栈中出栈的顺序一致。


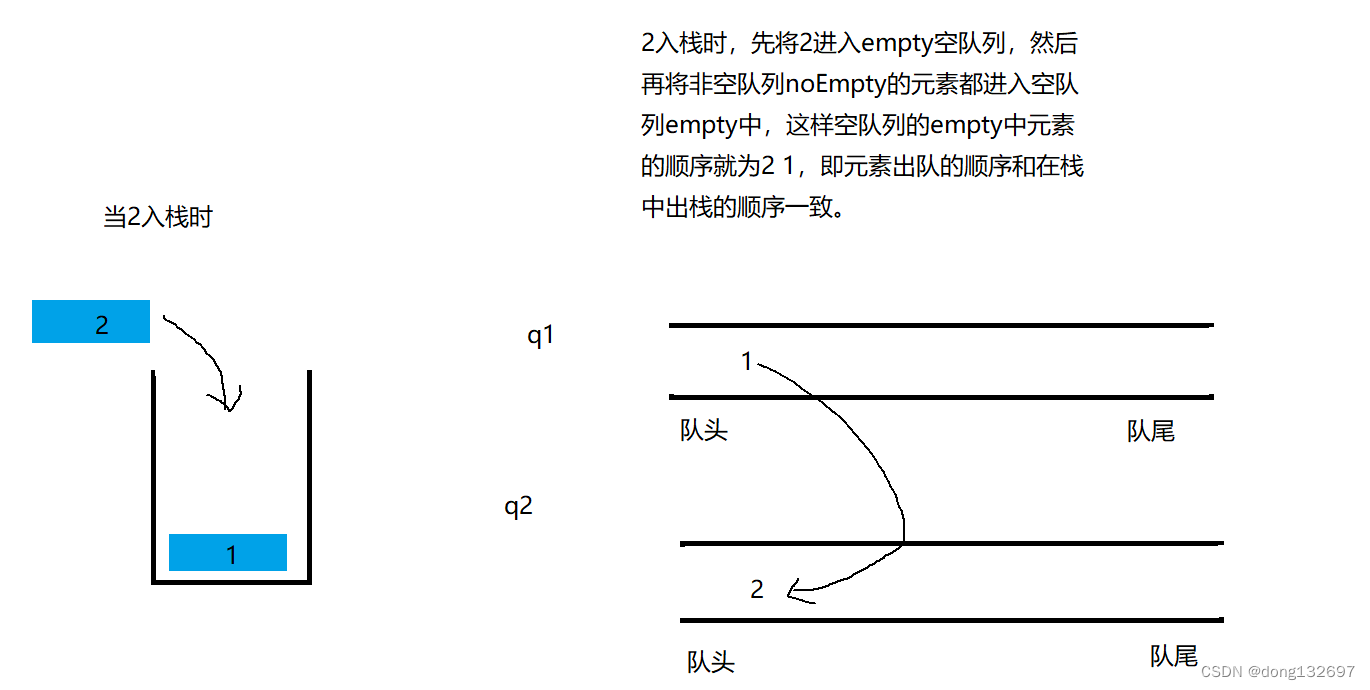
当再有元素入栈时，重复上述操作即可。

时间复杂度和空间复杂度

时间复杂度：入栈为O(N)，其余为O(1)
空间复杂度：O(N)

代码

该方法只有入栈和出栈还有返回栈顶元素的函数和第一种方法不同，只需将这三个函数改变即可。

void myStackPush(MyStack* obj, int x) {assert(obj);//先设q1为空队列，q2为非空队列Queue* emptyQ = &(obj->q1);Queue* noemptyQ = &(obj->q2);//如果q1非空，说明设错了，则改正。if(!QueueEmpty(&(obj->q1))){emptyQ = &(obj->q2);noemptyQ = &(obj->q1);}QueuePush(emptyQ,x);//将非空队列中的元素都进入空队列中while(QueueSize(noemptyQ)>0){QueuePush(emptyQ,QueueFront(noemptyQ));QueuePop(noemptyQ);}}int myStackPop(MyStack* obj) {//先判断栈是否为空，如果为空则不可以出栈assert(obj);assert(!myStackEmpty(obj));//先设q1为空队列，q2为非空队列Queue* emptyQ = &(obj->q1);Queue* noemptyQ = &(obj->q2);//如果q1非空，说明设错了，则改正。if(!QueueEmpty(&(obj->q1))){emptyQ = &(obj->q2);noemptyQ = &(obj->q1);}int top = QueueFront(noemptyQ);QueuePop(noemptyQ);return top;
}int myStackTop(MyStack* obj) {assert(obj);//此时非空队列中元素的顺序和出栈顺序一致，所以栈顶元素在队头assert(!myStackEmpty(obj));if(!QueueEmpty(&(obj->q1))){return QueueFront(&(obj->q1));}else{return QueueFront(&(obj->q2));}
}

方法三、

使用一个队列来实现栈。

实现思路

该方法只需要一个队列即可，当有元素要入栈时，在队列中的操作是将该元素先入队列，然后将该队列的队尾结点之前的结点都依次出队列再入队列，此时刚进入栈的元素即在队列的队头中，当要出栈时，直接将队头元素出队即可。

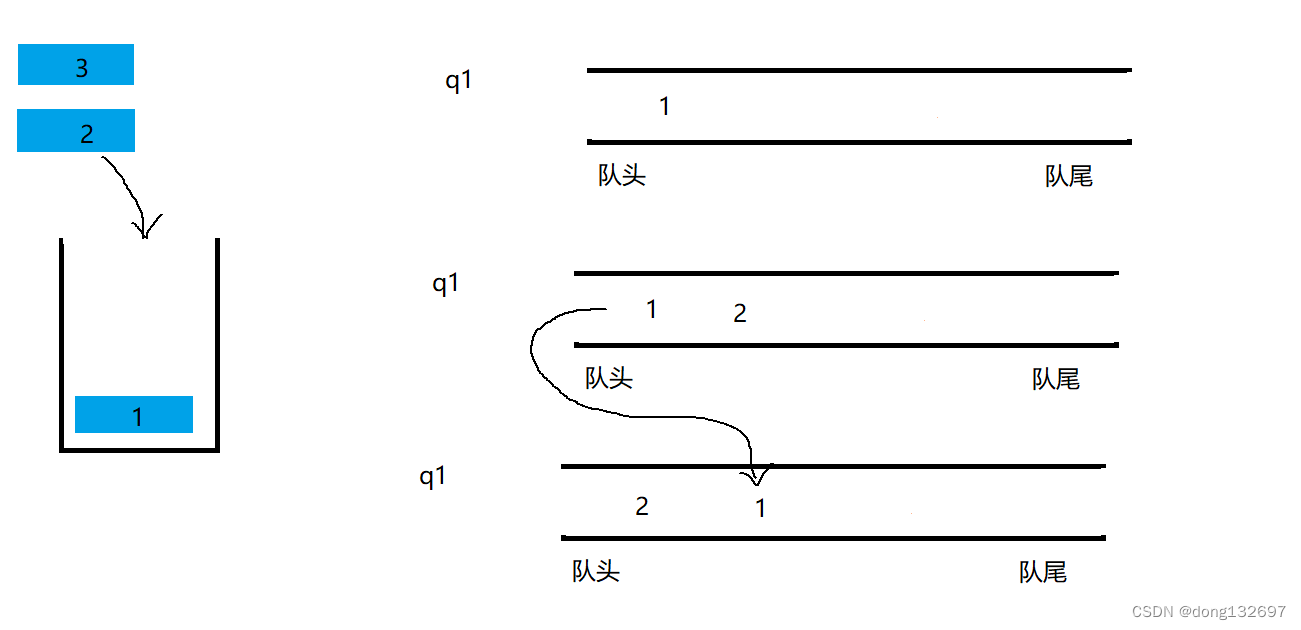
时间复杂度和空间复杂度

时间复杂度：入栈为O(N)，其余为O(1)
空间复杂度：O(1)

代码

该方法因为只用了一个结构体，所以栈结构体中只创建了一个队列

/该结构体采用了匿名结构体，然后将这个匿名结构体重命名为MyStack
typedef struct {//创建一个队列Queue q1;
} MyStack;
bool myStackEmpty(MyStack* obj);MyStack* myStackCreate() {//此时MyStack就相当于一个栈，当我们要使用一个栈时，先申请空间创建一个MyStack的结点MyStack* stack = (MyStack*)malloc(sizeof(MyStack));QueueInit(&(stack->q1));return stack;
}void myStackPush(MyStack* obj, int x) {assert(obj);//先将元素入队QueuePush(&(obj->q1),x);//然后将队列中队尾元素之前的结点都出队再入队int k = QueueSize(&(obj->q1))-1;while(k){QueuePush(&(obj->q1),QueueFront(&(obj->q1)));QueuePop(&(obj->q1));k--;}}int myStackPop(MyStack* obj) {//先判断栈是否为空，如果为空则不可以出栈assert(obj);assert(!myStackEmpty(obj));//此时队列中的队头元素即为栈顶元素int top = QueueFront(&(obj->q1));QueuePop(&(obj->q1));return top;
}int myStackTop(MyStack* obj) {assert(obj);//此时队列中的队头元素即为栈顶元素assert(!myStackEmpty(obj));return QueueFront(&(obj->q1));
}bool myStackEmpty(MyStack* obj) {assert(obj);//判断栈空就是判断队列是否为空return QueueEmpty(&(obj->q1));
}void myStackFree(MyStack* obj) {assert(obj);//先释放队列的空间，然后再释放obj的空间QueueDestroy(&(obj->q1));free(obj);
}

总结

用队列实现栈的第一种方法和第二种方法类似，不过一个是在入栈时进行处理，一个是在出栈时处理。而第三种方法只使用了一个队列，在入栈时做处理。