[LeetCode周赛复盘] 第 333 场周赛20230219
[LeetCode周赛复盘] 第 333 场周赛20230219
- 一、本周周赛总结
- 二、 [Easy] 6362. 合并两个二维数组 - 求和法
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 三、[Medium] 6365. 将整数减少到零需要的最少操作数
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 四、[Medium] 6364. 无平方子集计数
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 五、[Hard] 6363. 找出对应 LCP 矩阵的字符串
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 六、参考链接
一、本周周赛总结
- 滑铁卢之战,以为要1题下班了,最后做出了T2,后两道不会做,一次掉80分,排名两千多。
- T1 模拟。
- T2 记忆化搜索 / dp。
- T3 子集状压DP/背包。
- T4 构造/思维题。

二、 [Easy] 6362. 合并两个二维数组 - 求和法
链接: 6362. 合并两个二维数组 - 求和法
1. 题目描述
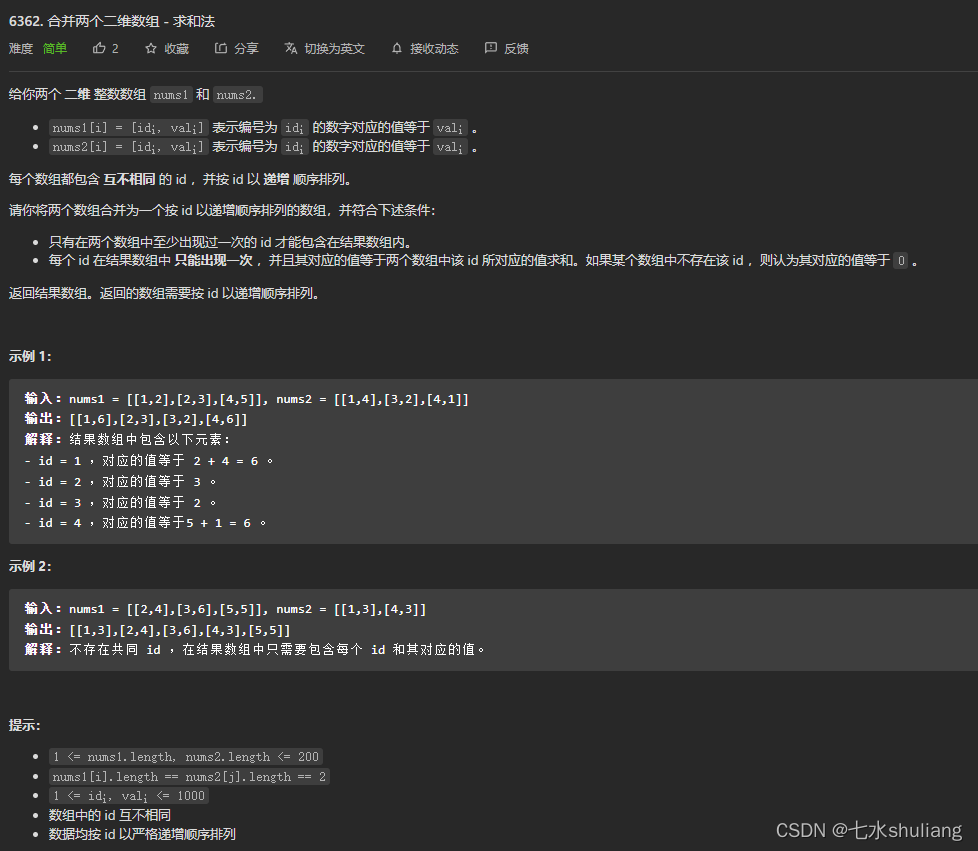
2. 思路分析
- 实际上题目考察归并排序,但是直接排序写得快。
3. 代码实现
class Solution:def mergeArrays(self, nums1: List[List[int]], nums2: List[List[int]]) -> List[List[int]]:cnt = Counter()for x,y in (nums1+nums2):cnt[x] += y return sorted([[k,v] for k,v in cnt.items()])
三、[Medium] 6365. 将整数减少到零需要的最少操作数
链接: 6365. 将整数减少到零需要的最少操作数
1. 题目描述

2. 思路分析
比赛时写了非常麻烦的两次DP。但都是在二进制串上dp的,因此复杂度是O(lgn)
- 把二进制串写出来,然后对连续的1分组,发现规律,如果是单独一个1可以直接1步减去,否则可以加lowbit然后1减去。
- 如果两组之间相隔仅1个0,可以尝试把这个0变成1,然后这两组一起加lowbit减去,共3步;但考虑到上一步已计算,因此这步多了2步,可以指直接讨论。
灵神的lowbit思路
- 从前往后讨论的比较复杂,其实从后往前讨论更方便一些,只需要考虑lowbit的加减即可。
3. 代码实现
记忆化搜索
@cache
def dfs(x):if x.bit_count() == 1:return 1lb = x & -x return 1 + min(dfs(x+lb),dfs(x-lb))
class Solution:def minOperations(self, n: int) -> int:return dfs(n)
dp
class Solution:def minOperations(self, n: int) -> int:s = bin(n)[2:]n = len(s)f = [0]*nf[0] = 1for i in range(1,n):if s[i] == '1':f[i] = f[i-1] + 1x = []p = 0for i,v in enumerate(f):if v == 0 and p != -1:x.append((p,i-1))p = -1if v == 1:p = iif p != -1:x.append((p,n-1))ans = [x[0][1]-x[0][0]+1,2]p = -2for i in range(1,len(x)):l,r = x[i]f = [0,0]f[0] = min(ans) + r-l+1f[1] = min(ans)+2if l - x[i-1][1] == 2:f[1] = min(f[1],ans[1]+1)ans = freturn min(ans)
四、[Medium] 6364. 无平方子集计数
链接: 6364. 无平方子集计数
1. 题目描述

2. 思路分析
- 这题是状压dp,比赛时想到了,但不会写。
- 其实灵神叫它:子集型状压DP。也就是枚举子集。
- 由于题目值域1~30很小,之间的质数共有10个可以先枚举出来,用10位来表示这10个质数是否被使用了。
- 然后对这30个数标记可以用的,再组合这些可以用的数,即合法的子集,求方案数。
- 状态就是哪些质数集合组成的乘积,它的方案数。
- 用刷表法转移:当处理一个合法数字时,若一个状态可以容纳这个数,那么组成的更大状态应该加上小状态的方案数。
- 这题里还学到了如何快速枚举mask子集,包括是否枚举空集的情况。
s = p # 枚举p的子集,不包含空集
while s:s = (s-1)&p
s = p # 枚举p的子集,包含空集
while True: s = (s-1)&pif s == p:break
3. 代码实现
PRIMES = 2,3,5,7,11,13,17,19,23,29
NSQ_TO_MASK = [0]*31 # 把2-30每个数都转化成它的质因子表示的位掩码
for i in range(2,31):for j, p in enumerate(PRIMES):if i % p == 0:if i%(p*p) == 0: # 如果含有平方因子则标记为否NSQ_TO_MASK[i] = -1breakNSQ_TO_MASK[i] |= 1<<j
MOD = 10**9+7
class Solution:def squareFreeSubsets(self, nums: List[int]) -> int:cnt = Counter(nums) # 计数M = 1 << len(PRIMES) # 掩码能组成状态的范围f = [0] * M # 每个状态的种类f[0] = 1 # 空方案数为1for x, c in cnt.items(): # 虽然是全部枚举,但是1的mask是0因此会跳过mask = NSQ_TO_MASK[x] # 取出掩码if mask > 0: # x是nsqother = (M-1)^mask # mask的补集j = other # 下面这一段是标准的枚举other补集(包括空集)的代码while True:f[j|mask] += f[j]*c # 补集加j的状态数应该累加上j的状态数f[j|mask] %= MOD j = (j-1)&otherif j == other:break # 由于是含空集,j会到0然后-1(二进制是全集),&other就==otherans = sum(f)*pow(2,cnt[1],MOD) - 1 # -1去掉空集return ans % MOD
五、[Hard] 6363. 找出对应 LCP 矩阵的字符串
链接: 6363. 找出对应 LCP 矩阵的字符串
1. 题目描述
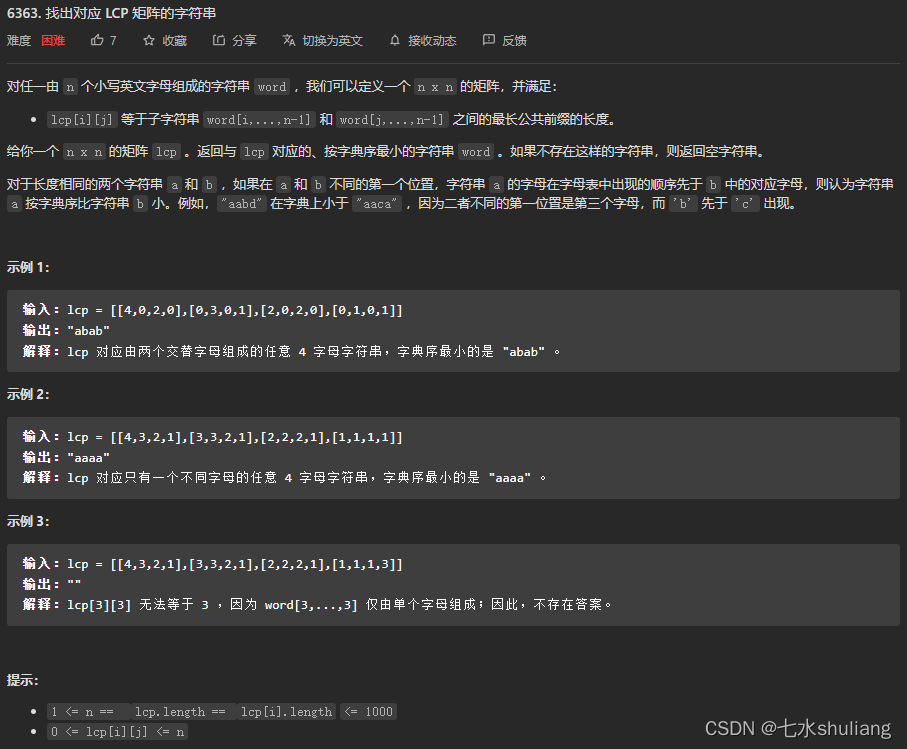
2. 思路分析
一道艰难的思维构造题。
- 首先s[0]肯定是a,否则造不出来答案。
- 并且所有lcp[i][j]不为0的位置,s[i] == s[j]。
- 所有位0的位置,字符必不可以相同。
- 那么从左到右填字符,优先填’a’,看lcp[0],即第一行,哪个数>0,则那个j也必须是a。
- 然后枚举b的位置,也从左做导游选第一个没填的位置;后续同理。
- 枚举完检查是否没填完,但字符用完了,就不合法。
- 最后在s中验证lcp数组,合法就返回s。
3. 代码实现
class Solution:def findTheString(self, lcp: List[List[int]]) -> str:n = len(lcp)s = [''] * n i = 0for c in ascii_lowercase: # 优先用小的字母while i < n and s[i]: # 找到还没填的位置i += 1if i == n:break s[i] = c # 直接填for j in range(i+1,n): # 和这个位置相同的位置都要填它if lcp[i][j]:s[j] = c if '' in s: # 如果字母都用完了还没填完就失败return ''# 在原数组上验证for i in range(n-1,-1,-1):for j in range(n-1,-1,-1):if s[i] == s[j]:if i == n-1 or j == n-1:if lcp[i][j] != 1:return ''else:if lcp[i][j] != lcp[i+1][j+1] + 1:return ''else:if lcp[i][j]:return ''return ''.join(s)
