当前位置：首页 > news >正文

Codeforces EDU 151 Div.2

news 2025/9/11 4:29:02

文章目录

- A. Forbidden Integer
- B. Come Together
- C. Strong Password
- D. Rating System
- E. Boxes and Balls

A. Forbidden Integer

Problem - A - Codeforces

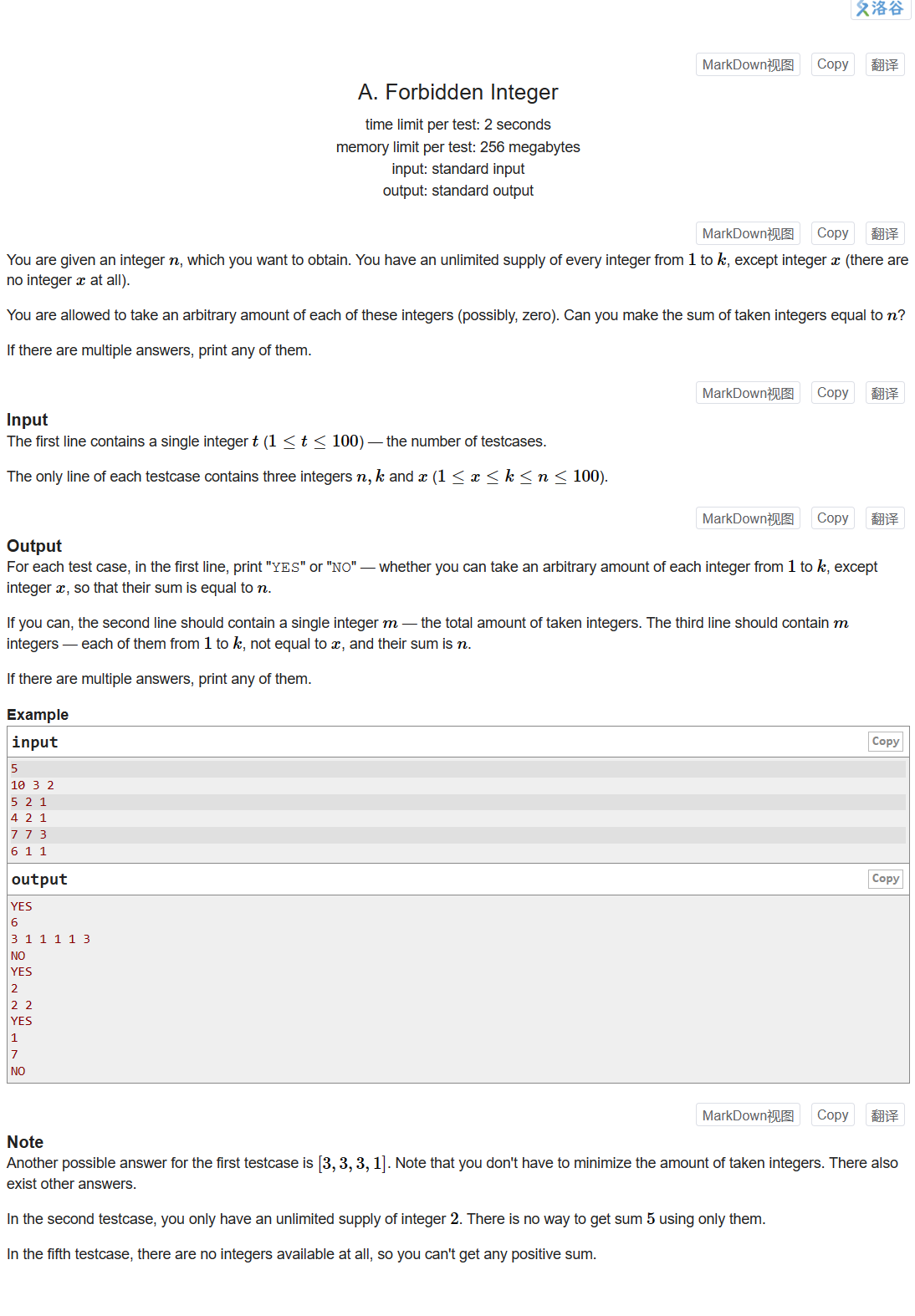
给定整数n，从1~k中选择除了x的数，使这些数之和为n，每个数可以选择无限次
爆搜，从k搜索到1，若当前搜索的数之和为n，返回true

#include <iostream>
using namespace std;const int N = 110;
int T, n, x, k;
int idx, p[N];bool dfs(int s, int start)
{if (start == -1) return false;if (s >= n) return s == n;for (int i = start; i >= 1; -- i ){if (i != x){p[idx ++ ] = i;if (dfs(s + i, start)) return true;idx -- ;}}return dfs(s, start - 1);
}int main()
{cin >> T;while ( T -- ){cin >> n >> k >> x;idx = 0;if (dfs(0, k)){puts("YES");cout << idx << endl;for (int i = 0; i < idx; ++ i ) cout << p[i] << ' ';cout << endl;}else puts("NO");}return 0;
}

B. Come Together

Problem - B - Codeforces

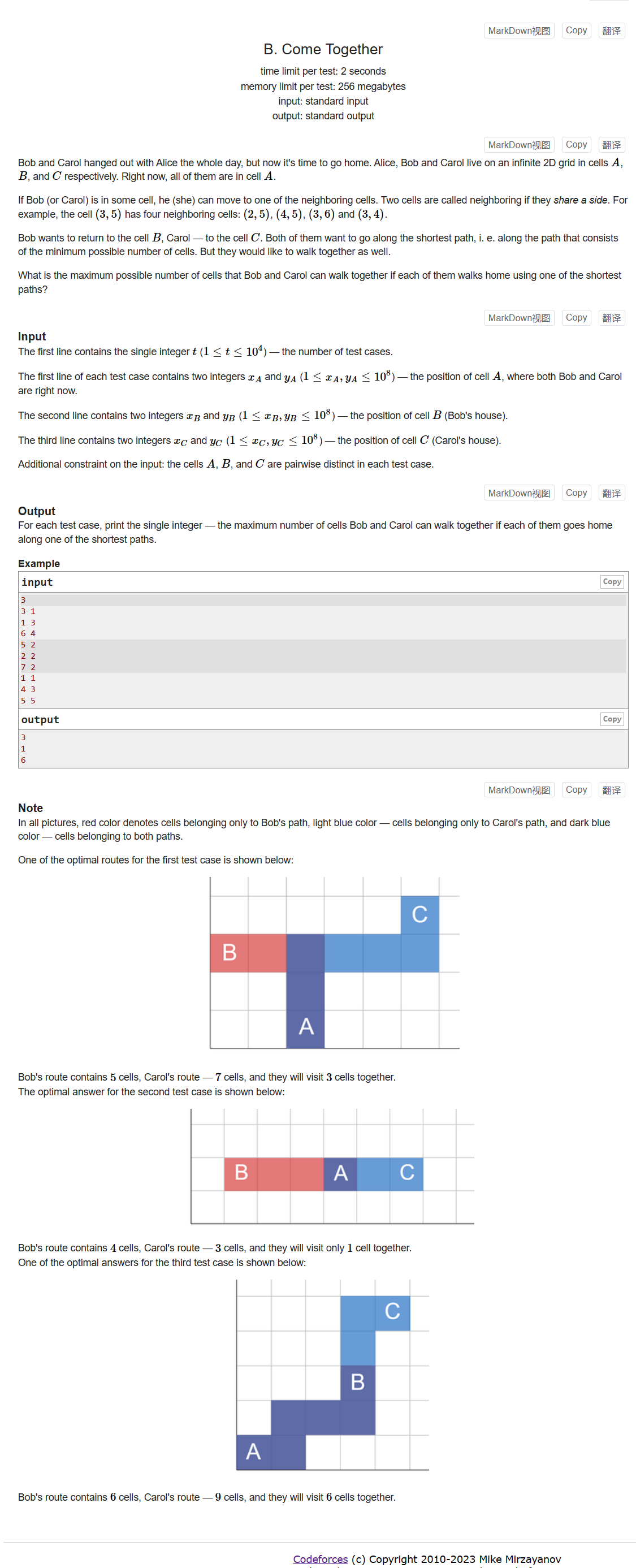
给定三个点，A为起点，BC为终点，从起点走到两个终点的最短路中，最长的公共路径长度是多少？
这是个我的错误思路：一开始以为是bfs最短路，想着在bfs的过程中记录路径
但是矩阵中没有障碍物，完全没有必要bfs，直接将起点于终点的横纵坐标之差相加，就是最短距离了
你可以发现，所有最短路中，无论怎么走，横向距离都是起点与终点的横坐标之差，当然纵向距离也是，所以有了以上结论
那么两条最短路的公共路径呢？将横纵方向分开来看，对于横坐标，若两者的终点都在起点的同一方向（都位于左边或左边），此时横向的最短距离等于横向距离离起点近的终点的横向距离，即 $min(x_b, x_c)$ 。若两者位于起点的左右两边，那么在横向距离上两者没有公共路径。同理，纵向距离也是如此

#include <iostream>
using namespace std;typedef long long LL;
LL T, xa, ya, xb, yb, xc, yc;int main()
{cin >> T;while ( T -- ){int ans = 0;cin >> xa >> ya >> xb >> yb >> xc >> yc;xb -= xa, yb -= ya, xc -= xa, yc -= ya; // 以a为源点if ((xb > 0) == (xc > 0)) ans += min(abs(xb), abs(xc));if ((yb > 0) == (yc > 0)) ans += min(abs(yb), abs(yc));cout << ans + 1 << endl;}return 0;
}

debug：若用xb * xc > 0判断两点是否位于源点的同一方向，相乘会爆int

C. Strong Password

Problem - C - Codeforces

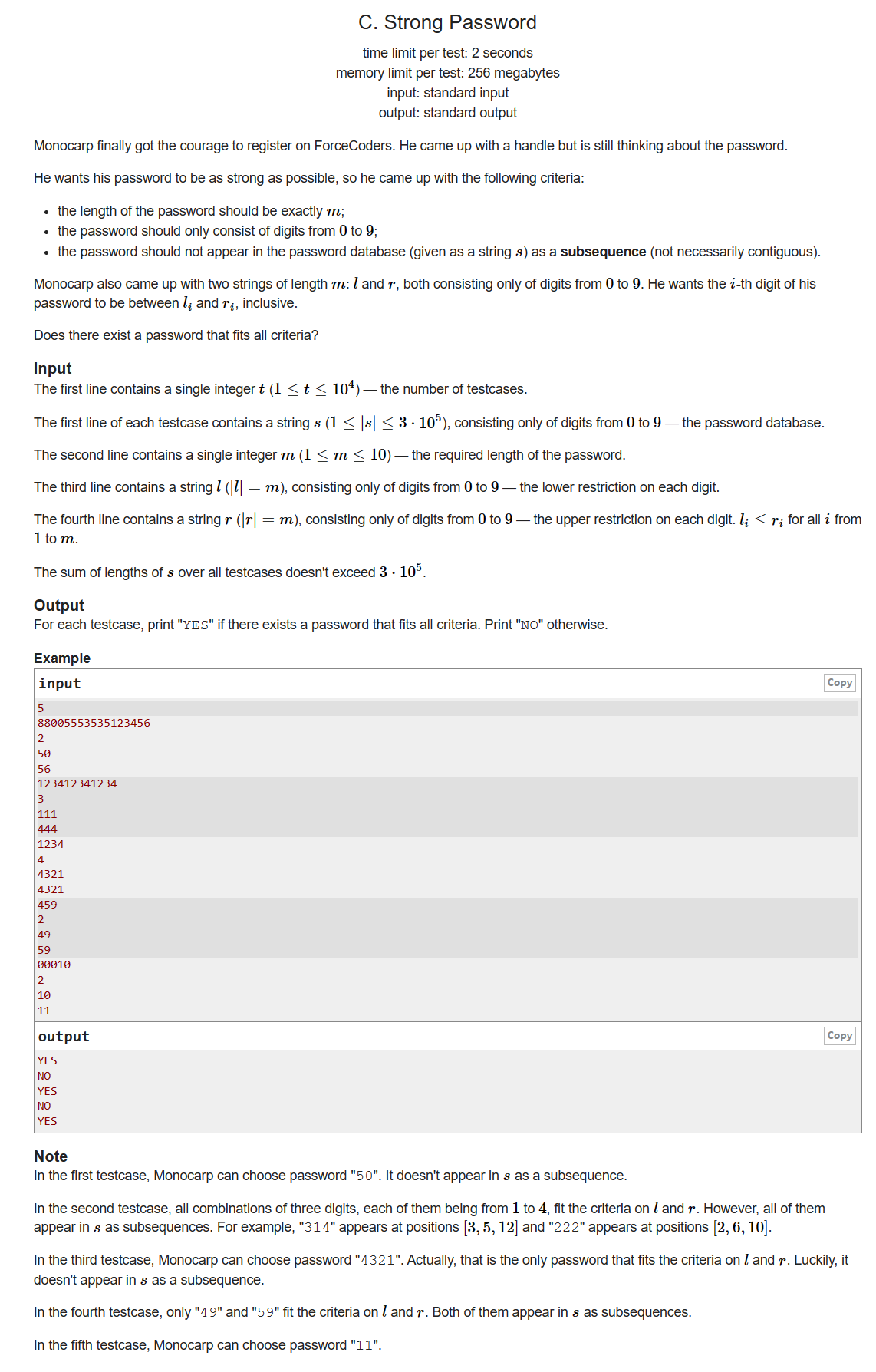
题目只要求输出YES和NO，没有要求输出具体的序列，所以这题不用想得太复杂
比较暴力的解法是枚举所有可能的序列，用爆搜判断该序列是否为s的子序列，只要有一个序列不是s的子序列就输出YES，否则输出NO
考虑暴力如何优化？两个优化方向：枚举所有可能的序列和爆搜判断

枚举所有可能的序列不太好优化
关于爆搜的优化：由于s中只有字符1_{9，可以预处理出第i个字符右边（包括第i个字符），1}9第一次出现的位置，若没有出现，位置用无穷表示
枚举t串时，t串的每个字符都有一个范围，假设t串的字符在s串中出现的下标为 $x$ ，若 $x$ 越大，s串中用来组成t串的字符就越少，出现相同子序列的概率就越低
以上贪心策略用反证法可以证明正确性，因此对于t串的每个字符，根据每个字符的范围以及字符在s串中出现的位置，确定一个下标最大的字符即可
遇到无穷直接输出YES即可

#include <iostream>
#include <cstring>
using namespace std;const int N = 3e5 + 10, M = 15;
char s[N], l[M], r[M];
int last[N][M], T, m;int main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cin >> T;while ( T -- ){cin >> s >> m >> l >> r;int len = strlen(s);memset(last[len], 0x3f, sizeof last[len]);for (int i = len - 1; i >= 0; -- i ){memcpy(last[i], last[i + 1], sizeof last[i + 1]);last[i][s[i] - '0'] = i;}int cur = -1; // cur和next为搜索s串的双指针for (int i = 0; i < m && cur != 0x3f3f3f3f; ++ i ){int next = 0;for (int j = l[i] - '0'; j <= r[i] - '0'; ++ j ){next = max(next, last[cur + 1][j]);}   cur = next;}cout << (cur == 0x3f3f3f3f ? "YES\n" : "NO\n");}return 0;
}

debug：如果memset(last[len], 0x3f, sizeof last[len])写成memset(last, 0x3f, sizeof last)，直接memset整个last数组会TLE的，考虑到预处理的顺序，只要初始化最后一个一维数组即可last[len]

D. Rating System

Problem - D - Codeforces

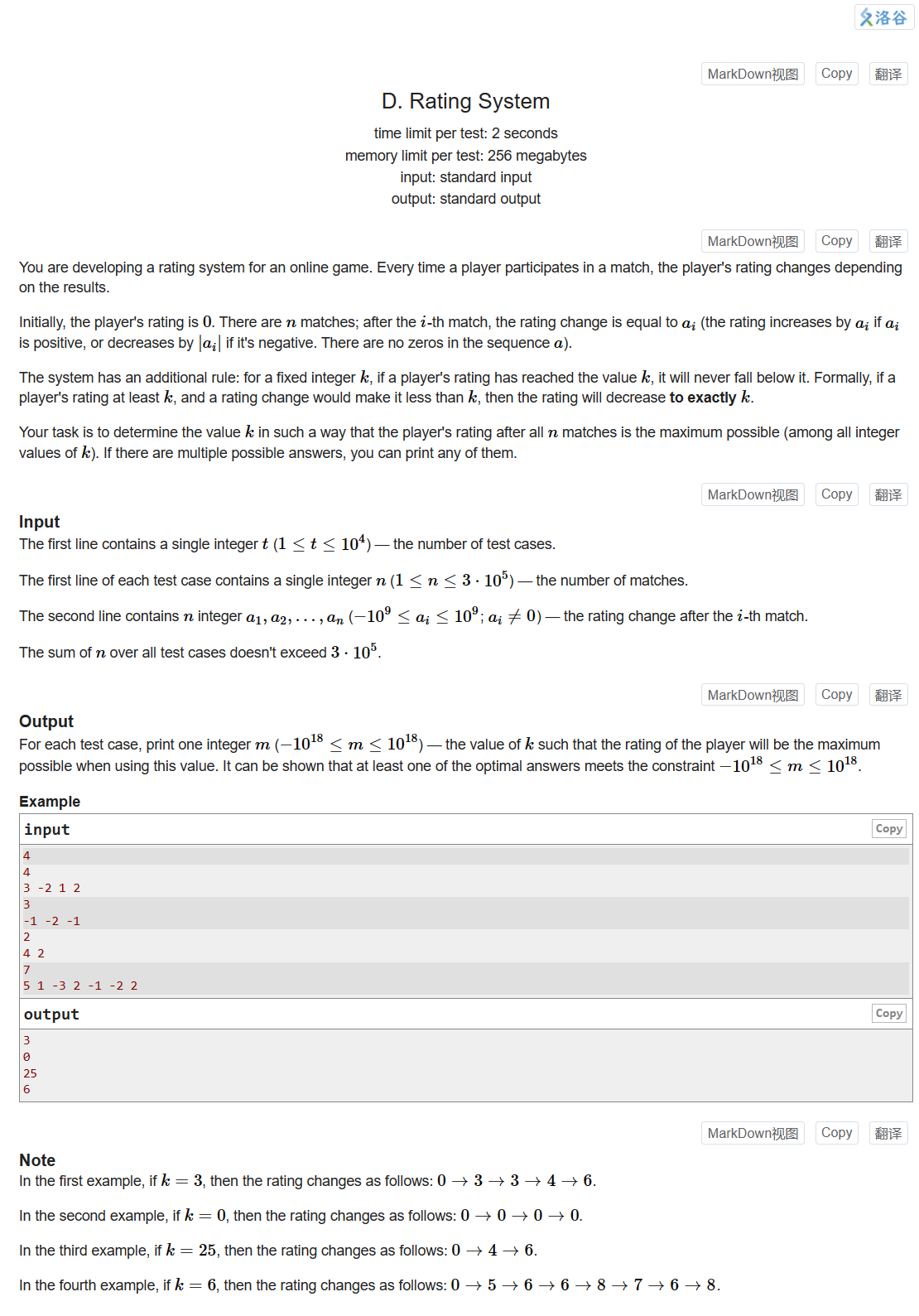
看着像是求最大子段和，一开始也是这么想的，但是仔细一想却是不对的
参考视频：最小子段和动态规划【Codeforces EDU 151】_哔哩哔哩_bilibili

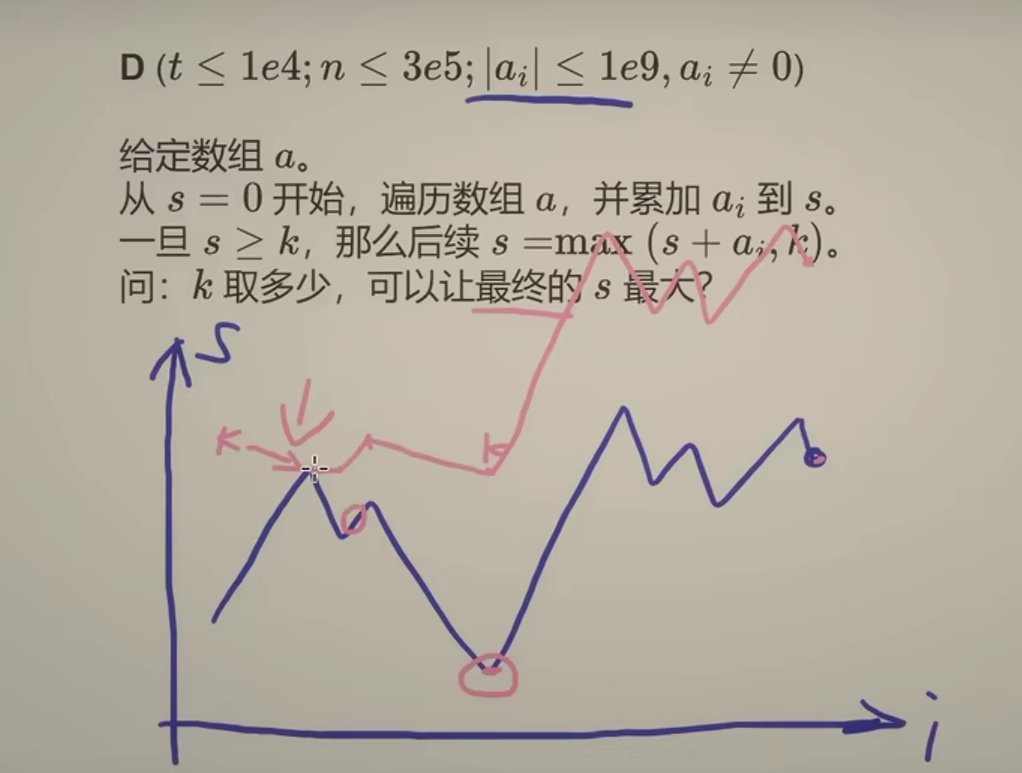
确定一个k值，使分数大于等于k值后不会小于k值，也就是说：抵消分数递达k之后的减分行为
问k为多少，最后的分数最高？显然，抵消的分数越多，最后的分数越高
题目给定每一次分数的变化，即用 $a_i$ 的正负表示分数的加减变化。若要抵消最多的减分，就要找出数组中的最小连续子段和 $a_i, a_r]$ ，再将k设置为 $sum(a_0, a_{i-1})$
通常求最小子段和，都是使用dp，然而这题求的并不是具体的最小子段和，这题求的是最小子段和的左区间，以及一个前缀和信息。因此只需要在求前缀和的过程中，维护最小子段和的左区间信息即可

#include <iostream>
using namespace std;typedef long long LL;
const int N = 3e5 + 10;
int a[N], T;int main()
{cin >> T;while ( T -- ){int n;cin >> n;for (int i = 0; i < n; ++ i ) cin >> a[i];LL ans = 0, sum = 0, cmax = 0, k;for (int i = 0; i < n; ++ i ){sum += a[i];cmax = max(cmax, sum);LL val = cmax - sum;if (ans < val){ans = val;k = cmax;}}cout << k << endl;}return 0;
}