第三章 图论 No.13拓扑排序
文章目录
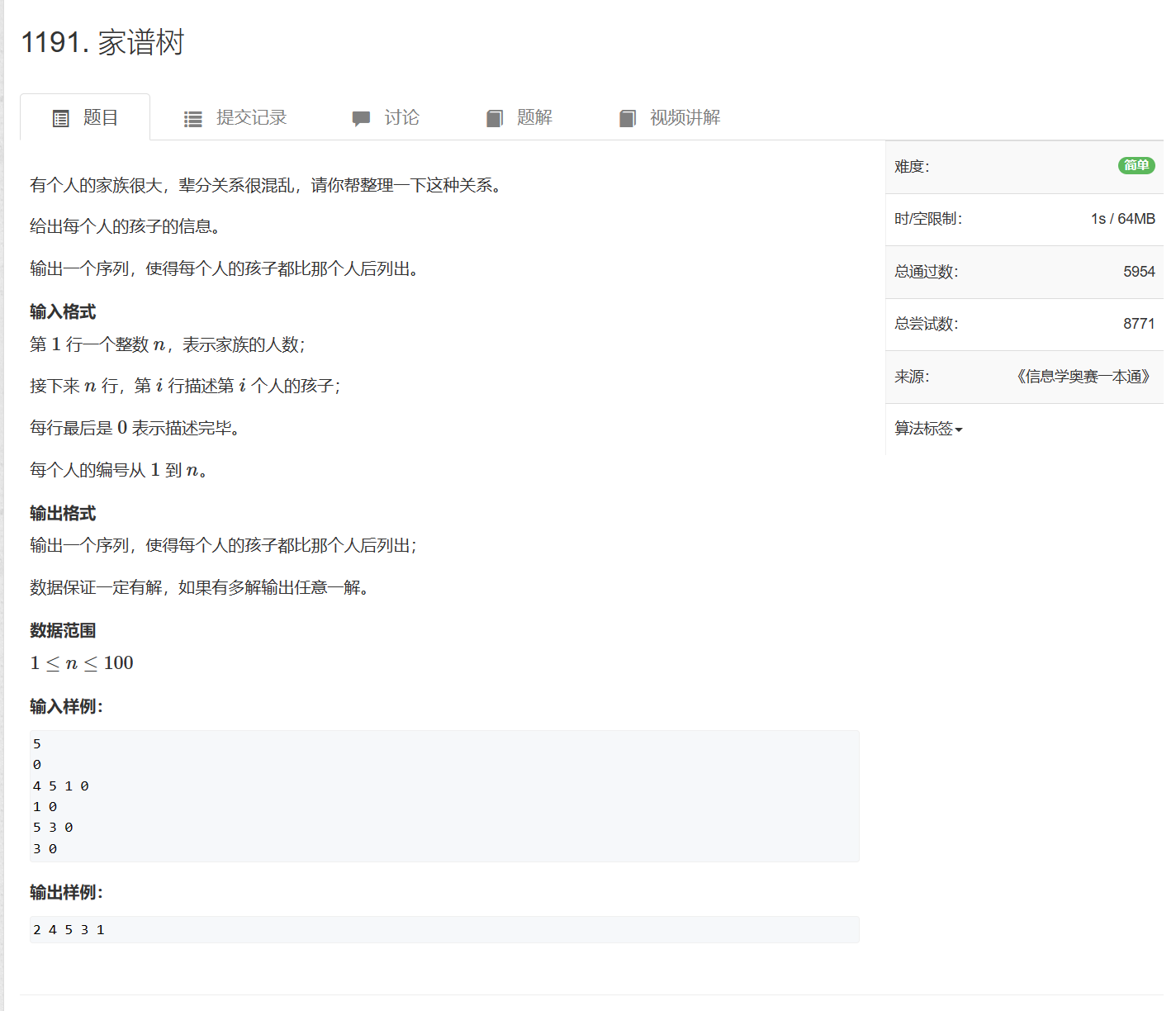
- 裸题:1191. 家谱树
- 差分约束+拓扑排序:1192. 奖金
- 集合+拓扑序:164. 可达性统计
- 差分约束+拓扑序:456. 车站分级
拓扑序和DAG有向无环图联系在一起,通常用于最短/长路的线性求解

裸题:1191. 家谱树
1191. 家谱树 - AcWing题库
#include <iostream>
#include <cstring>
using namespace std;const int N = 110, M = 10010;
int h[N], e[M], ne[M], idx;
int d[N], q[N], hh, tt = -1;
int n, m;void add(int x, int y)
{e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}void topsort()
{for (int i = 1; i <= n; ++ i )if (!d[i]) q[ ++ tt ] = i;while (tt >= hh ){int x = q[hh ++ ];for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (-- d[y] == 0) q[++ tt] = y;}}
}int main()
{memset(h, -1, sizeof(h));scanf("%d", &n);for (int x = 1; x <= n; ++ x ){int y;while (scanf("%d", &y), y){add(x, y);d[y] ++ ;}}topsort();for (int i = 0; i <= tt; ++ i )printf("%d ", q[i]);return 0;
}
差分约束+拓扑排序:1192. 奖金
1192. 奖金 - AcWing题库
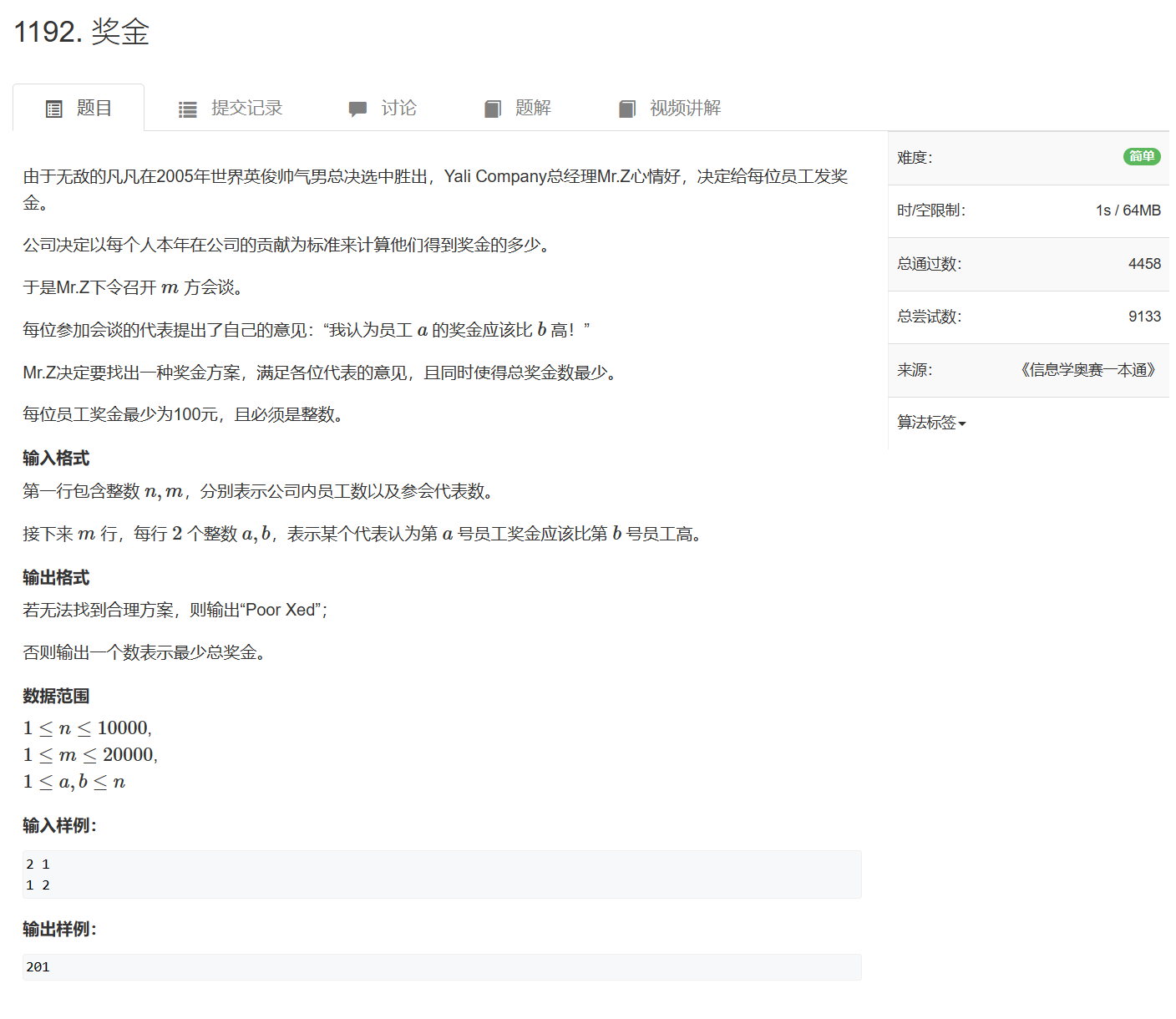
由于图中所有边权都是正数,可以直接使用topsort求解差分约束问题
根据题意,要求一个最小值,使用最长路求解,转化题目的条件: A > = B + 1 A >= B + 1 A>=B+1与 x i > = x 0 + 100 x_i >= x_0 + 100 xi>=x0+100
x 0 x_0 x0为一个虚拟源点,向每个点连了一条权值为100的边
若图中存在环,topsort的队列长度将小于n,因为环的起点无法进入队列
先用topsort判断图中是否存在环,若不存在,根据拓扑序遍历图,求解最长路
#include <iostream>
#include <cstring>
using namespace std;const int N = 10010, M = 30010;
int h[N], e[M], ne[M], w[M], idx;
int q[N], d[N], hh, tt = -1;
int dis[N];
int n, m;void add(int x, int y, int d)
{e[idx] = y, ne[idx] = h[x], w[idx] = d, h[x] = idx ++ ;
}bool topsort()
{q[ ++ tt ] = 0;while (tt >= hh){int x = q[hh ++ ];for (int i = h[x]; i != -1; i = ne[i] ){int y = e[i];if ( -- d[y] == 0) q[ ++ tt ] = y;}}return tt == n;
}int main()
{memset(h, -1, sizeof(h));scanf("%d%d", &n, &m);for (int i = 0; i < m; ++ i ){int x, y;scanf("%d%d", &x, &y);add(y, x, 1);d[x] ++ ;}for (int i = 1; i <= n; ++ i ) add(0, i, 100), d[i] ++ ;if (!topsort()) puts("Poor Xed");else {for (int k = 0; k <= tt; ++ k ){int x = q[k];for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];dis[y] = max(dis[y], dis[x] + w[i]);}}int sum = 0;for (int i = 1; i <= n; ++ i ) sum += dis[i];printf("%d\n", sum);}return 0;
}
debug:最后的遍历没有按照拓扑序
for (int x = 0; x <= tt; ++ x )
{for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];dis[y] = max(dis[y], dis[x] + w[i]);}
}
集合+拓扑序:164. 可达性统计
[164. 可达性统计 - AcWing题库](https://www.acwing.com/problem/content/description/166/
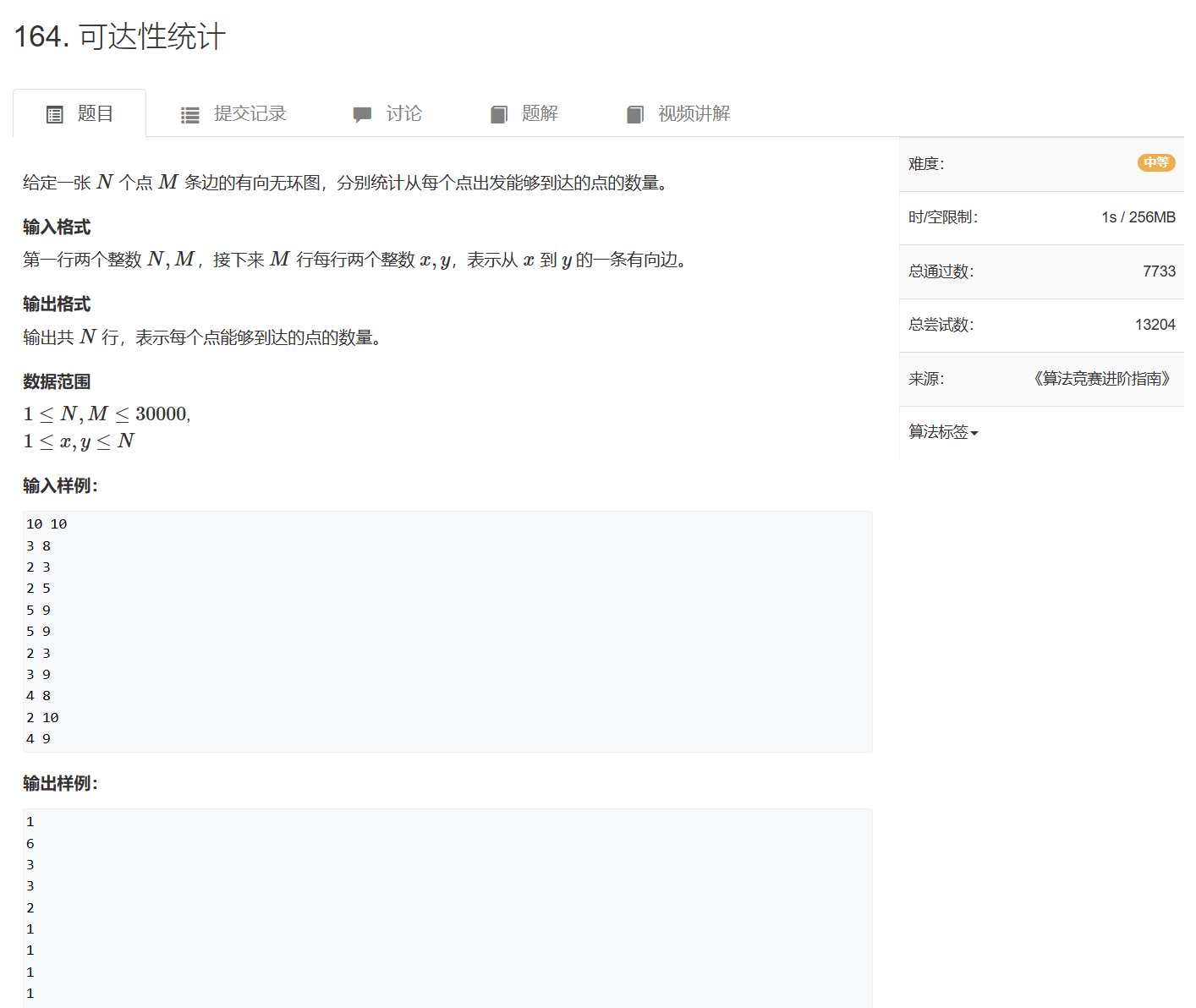
从集合的角度思考, f ( i ) f(i) f(i)表示i这个点能到达的所有点,i首先能到达自己,其次能达到 f ( j 1 ) , f ( j 2 ) , . . . , f ( j n ) f(j_1), f(j_2), ... , f(j_n) f(j1),f(j2),...,f(jn),假设i与n个点直接相连
那么要求 f ( i ) f(i) f(i),就必须求出 f ( j 1 ) , f ( j 2 ) , . . . , f ( j n ) f(j_1), f(j_2), ... , f(j_n) f(j1),f(j2),...,f(jn),即拓扑排序中位于i之后的所有点的 f ( j ) f(j) f(j)
所以这题先拓扑排序,再根据拓扑排序的逆序,求 f ( i ) f(i) f(i)
如何表示集合 f ( i ) f(i) f(i)?用STL的容器bitset,假设图中有N个点,那么bitset的长度为N,每个点都用一个bitset记录其集合,1表示i能递达这个点,0表示不能递达
那么 f ( i ) = f ( j 1 ) ∩ f ( j 2 ) ∩ . . . ∩ f ( j n ) f(i) = f(j_1)∩ f(j_2)∩ ...∩f(j_n) f(i)=f(j1)∩f(j2)∩...∩f(jn)
关于bitset的使用,bitset之间支持|=运算,count()输出bitset中1的个数
#include <iostream>
#include <cstring>
#include <bitset>
using namespace std;const int N = 30010, M = N;
int h[N], e[M], ne[M], idx;
int q[N], d[N], hh, tt = -1;
bitset<N> f[N];
int n, m;void add(int x, int y)
{e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}void topsort()
{for (int i = 1; i <= n; ++ i )if (!d[i]) q[ ++ tt ] = i;while (tt >= hh){int x = q[hh ++ ];for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if ( -- d[y] == 0) q[ ++ tt ] = y;}}
}int main()
{memset(h, -1, sizeof(h));scanf("%d%d", &n, &m);for (int i = 0; i < m; ++ i ){int x, y;scanf("%d%d", &x, &y);add(x, y);d[y] ++ ;}topsort();for (int i = tt; i >= 0; -- i ){int x = q[i];f[x][x] = 1;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];f[x] |= f[y];}}for (int i = 1; i <= n; ++ i ) printf("%d\n", f[i].count());return 0;
}
差分约束+拓扑序:456. 车站分级
456. 车站分级 - AcWing题库
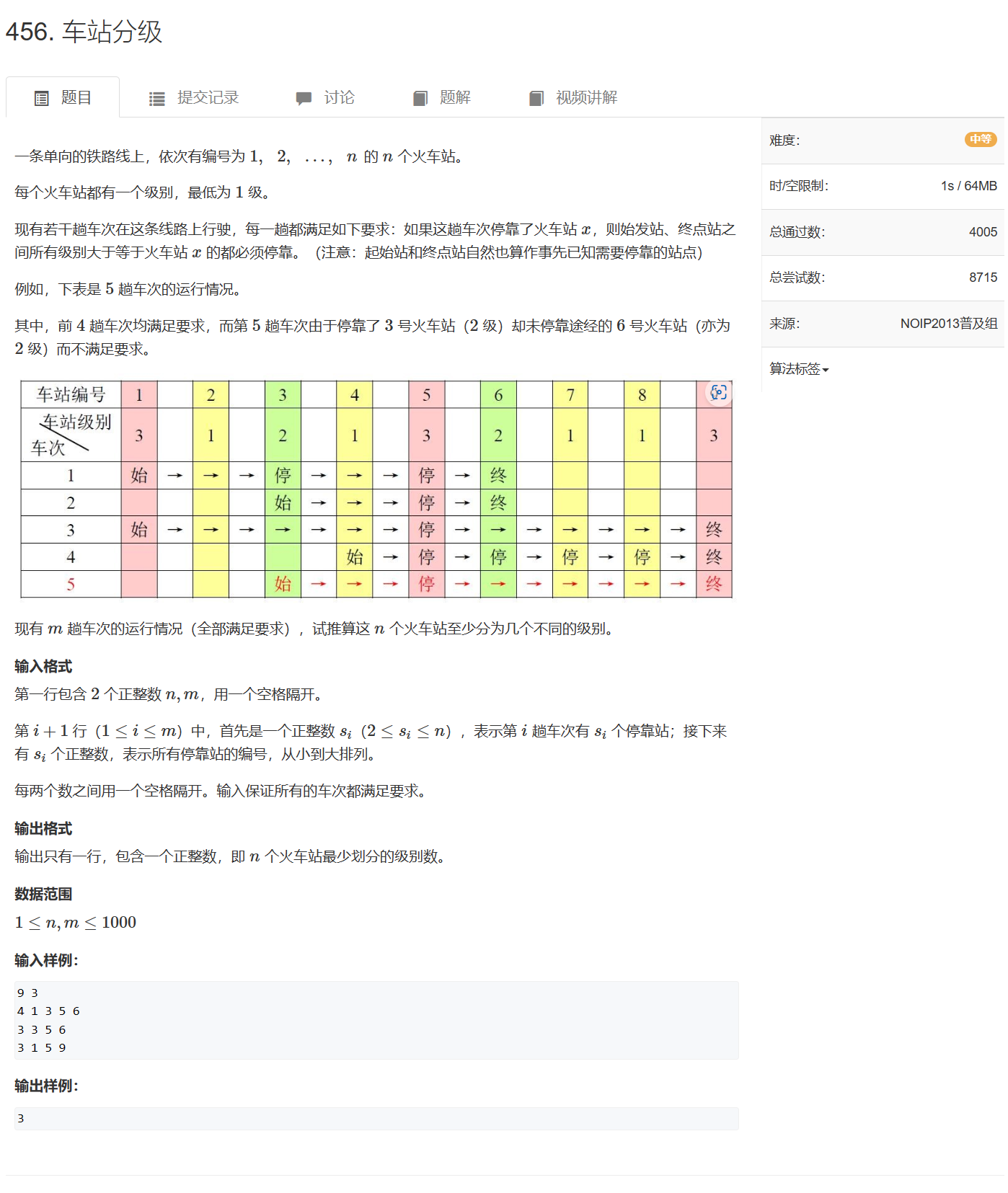
分析题意:对于每一条路线,未经过的站点的等级一定小于经过的站点等级,并且最低的站点等级为1级
题目要求所有等级划分中的最少等级数,用最长路求最小值。将以上条件转换成差分约束中的两个条件: B > = A + 1 B >= A + 1 B>=A+1, x i > = x 0 + 1 x_i >= x_0 + 1 xi>=x0+1
x 0 x_0 x0为虚拟源点,通过 x 0 x_0 x0能到达图中的所有点,那么就一定能递达所有边
由于每条路线路都会建立n * m条边,极端情况下可能会爆空间,所以考虑如何优化
一条路径中未经过的站点将向经过的站点连接一条权值为1的边,一共n * m条,由于这些边的权值相同,可以在这些边中创建一个虚拟点v,未经过的点分别向v连一条权值为0的边,v向经过的点分别连接一条权值为1的边。这样,从未经过的点到经过的点的权值和依然为1,但是需要建立的边数为n + m,此时的边数在极端情况下也不会爆空间
#include <iostream>
#include <cstring>
using namespace std;const int N = 2010, M = 1e6 + 10;
int h[N], e[M], ne[M], w[M], idx;
int d[N], q[N], hh, tt = -1;
bool st[N]; int dis[N];
int n, m;void add(int x, int y, int d)
{e[idx] = y, ne[idx] = h[x], w[idx] = d, h[x] = idx ++ ;
}void topsort()
{for (int i = 1; i <= n + m; ++ i ) if (!d[i]) q[ ++ tt ] = i;while (tt >= hh){int x = q[hh ++ ];for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (-- d[y] == 0) q[ ++ tt ] = y;}}
}int main()
{memset(h, -1, sizeof(h));scanf("%d%d", &n, &m);for (int i = 1; i <= m; ++ i ){memset(st, false, sizeof(st));int t, start = n, end = 0;scanf("%d", &t);while (t -- ){int x;scanf("%d", &x);st[x] = true;start = min(start, x), end = max(end, x);}int v = n + i;for (int i = start; i <= end; ++ i ){if (st[i]) add(v, i, 1), d[i] ++ ;else add(i, v, 0), d[v] ++ ;}}topsort();for (int i = 1; i <= n; ++ i ) dis[i] = 1;for (int i = 1; i <= tt; ++ i ){int x = q[i];for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];dis[y] = max(dis[y], dis[x] + w[i]);}}int res = 0;for (int i = 1; i <= n; ++ i ) res = max(res, dis[i]);printf("%d\n", res);return 0;
}
debug:w[M]写成了w[N],又是这样,然后debug了半天,了
