Hands on RL 之 Off-policy Maximum Entropy Actor-Critic (SAC)

​ Soft actor-critic方法又被称为Off-policy maximum entropy actor-critic algorithm。

1. 理论基础

1.1 Maximum Entropy Reinforcement Learning, MERL

​ 在MERL原论文中，引入了熵的概念，熵定义如下：

随机变量$x$符合$P$的概率分布，那么随机变量$x$的熵$\mathcal{H}(P)$为
$$\mathcal{H}(P)={\mathbb{E}}_{x\sim P}[-\log p(x)]$$
标准的RL算法的目标是能够找到最大化累计收益的策略
$${\pi }_{\text{std}}^{\ast }=\arg \underset{\pi }{\max }\sum _t{\mathbb{E}}_{(s_t,a_t)\sim {\rho }_{\pi }}[r(s_t,a_t)]$$
引入了熵最大化的RL算法的目标是
$${\pi }_{MERL}^{\ast }=\arg \underset{\pi }{\max }\sum _t{\mathbb{E}}_{(s_t,a_t)\sim {\rho }_{\pi }}[r(s_t,a_t)+\alpha \mathcal{H}(\pi (\cdot |s_t))]$$
其中，${\rho }_{\pi }$表示在策略$\pi$下状态空间对的概率分布，$\alpha$是温度系数，用于调节对熵的重视程度。

类似的，我们也可以在RL的动作值函数，和状态值函数中同样引入熵的概念。

标准的RL算法的值函数
$$\begin{array}{rl}\text{standard Q function:}{Q}^{\pi }(s,a)& ={\mathbb{E}}_{s_t,a_t\sim {\rho }_{\pi }}[\sum _{t=0}^{\infty }{\gamma }^{t}r(s_t,a_t)|s_0=s,a_0=a]\\ \text{standard V function:}{V}^{\pi }(s)& ={\mathbb{E}}_{s_t,a_t\sim {\rho }_{\pi }}[\sum _{t=0}^{\infty }{\gamma }^{t}r(s_t,a_t)|s_0=s]\end{array}$$

根据MERL的目标函数，在值函数中引入熵的概念之后就获得了Soft Value Function, SVF
$$\begin{array}{rl}\text{Soft Q function:}{Q}_{\text{soft}}^{\pi }(s,a)& ={\mathbb{E}}_{s_t,a_t\sim {\rho }_{\pi }}[\sum _{t=0}^{\infty }{\gamma }^{t}r(s_t,a_t)+\alpha \sum _{t=1}^{\infty }{\gamma }^t\mathcal{H}(\pi (\cdot |s_t))|s_0=s,a_0=a]\\ \text{Soft V function:}{V}_{\text{soft}}^{\pi }(s)& ={\mathbb{E}}_{s_t,a_t\sim {\rho }_{\pi }}[\sum _{t=0}^{\infty }{\gamma }^t(r(s_t,a_t)+\alpha \mathcal{H}(\pi (\cdot |s_t)))|s_0=s]\end{array}$$

观察上式我们就可以获得Soft Bellman Equation
$$\begin{gathered} \begin{array}{rl}{Q}_{\text{soft}}^{\pi }(s,a)& ={\mathbb{E}}_{s^{\prime }\sim p(s^{\prime }|s,a) \\ {a}^{\prime }\sim \pi }[r(s,a)+\gamma (Q_{\text{soft}}^{\pi }(s^{\prime },a^{\prime })+\alpha \mathcal{H}(\pi (\cdot |s^{\prime })))]\\ & ={\mathbb{E}}_{s^{\prime }\sim p(s^{\prime }|s,a)}[r(s,a)+\gamma V_{\text{soft}}^{\pi }(s)]\end{array} \end{gathered}$$

$$\begin{array}{rl}{V}_{\text{soft}}^{\pi }(s)& ={\mathbb{E}}_{s_t,a_t\sim {\rho }_{\pi }}[\sum _{t=0}^{\infty }{\gamma }^t(r(s_t,a_t)+\alpha \mathcal{H}(\pi (\cdot |s_t)))|s_0=s]\\ & ={\mathbb{E}}_{s_t,a_t\sim {\rho }_{\pi }}[\sum _{t=0}^{\infty }{\gamma }^{t}r(s_t,a_t)+\alpha \sum _{t=1}^{\infty }{\gamma }^t\mathcal{H}(\pi (\cdot |s_t))+\alpha \mathcal{H}(\pi (\cdot |s_t)|s_0=s]\\ & ={\mathbb{E}}_{s_t,a_t\sim {\rho }_{\pi }}[Q_{\text{soft}}^{\pi }(s,a)|s_0=s,a_0=a]+\alpha \mathcal{H}(\pi (\cdot |s_t))\\ & ={\mathbb{E}}_{a\sim \pi }[Q_{\text{soft}}^{\pi }(s,a)-\alpha \log \pi (a|s)]\end{array}$$

1.2 Soft Policy Evaluation and Soft Policy Improvement in SAC

soft Q function的值迭代公式
$$\begin{gathered} \begin{array}{rl}{Q}_{\text{soft}}^{\pi }(s,a)& ={\mathbb{E}}_{s^{\prime }\sim p(s^{\prime }|s,a) \\ {a}^{\prime }\sim \pi }[r(s,a)+\gamma (Q_{\text{soft}}^{\pi }(s^{\prime },a^{\prime })+\alpha \mathcal{H}(\pi (\cdot |s^{\prime })))]\\ & ={\mathbb{E}}_{s^{\prime }\sim p(s^{\prime }|s,a)}[r(s,a)+\gamma V_{\text{soft}}^{\pi }(s)]\end{array}\text{\hspace{1em}(1.1)(1.2)} \end{gathered}$$

soft V function的值迭代公式

$$V_{\text{soft}}^{\pi }(s)={\mathbb{E}}_{a\sim \pi }[Q_{\text{soft}}^{\pi }(s,a)-\alpha \log \pi (a|s)]\text{\hspace{1em}(1.3)}$$

在SAC中如果我们只打算维持一个Q值函数，那么使用式子$(1,1)$进行值迭代即可，

如果需要同时维持Q，V两个函数，那么使用式子$(1,2),(1,3)$进行值迭代。

下面直接给出训练中的损失函数

V值函数的损失函数

$$J_{V(\psi )}={\mathbb{E}}_{s_t\sim \mathcal{D}}[\frac{1}{2}(V_{\psi }(s_t)-{\mathbb{E}}_{a_t\sim {\pi }_{\varphi }}[Q_{\theta }(s_t,a_t)-\log {\pi }_{\varphi }(a_t|s_t)]{)}^2]$$

Q值函数的损失函数

$$\begin{gathered} J_{Q(\theta )}={\mathbb{E}}_{(s_t,a_t)\sim \mathcal{D}}\left[\frac{1}{2}\right(Q_{\theta }(s_t,a_t)-\hat{Q}(s_t,a_t)\left)\right] \\ \hat{Q}(s_t,a_t)=r(s_t,a_t)+\gamma {\mathbb{E}}_{s_{t+1}\sim p}[V_{\psi }(s_{t+1})] \\ \hat{Q}(s_t,a_t)=r(s_t,a_t)+\gamma Q_{\theta }(s_{t+1},a_{t+1}) \end{gathered}$$

策略$\pi$的损失函数

$$J_{\pi }(\varphi )={\mathbb{E}}_{s_t\sim \mathcal{D}}\left[{\mathbb{D}}_{KL}\right({\pi }_{\varphi }(\cdot |s_t)|\left|\frac{\exp (Q_{\theta }(s_t,\cdot ))}{Z_{\theta }(s_t)}\right)]$$

其中，$Z_{\theta }(s_t)$是分配函数 (partition function)

KL散度的定义如下

​ 假设对随机变量$\xi$，存在两个概率分布P和Q，其中P是真实的概率分布，Q是较容易获得的概率分布。如果$\xi$是离散的随机变量，那么定义从P到Qd KL散度为

$${\mathbb{D}}_{KL}(P||Q)=\sum _{i}P(i)\ln (\frac{P(i)}{Q(i)})$$

如果$\xi$是连续变量，则定义从P到Q的KL散度为

$${\mathbb{D}}_{KL}(P||Q)={\int }_{-\infty }^{\infty }p(x)\ln (\frac{p(x)}{q(x)})dx$$

那么根据离散的KL散度定义，我们可以将策略$\pi$的损失函数展开如下

$$\begin{array}{rl}{J}_{\pi }(\varphi )& ={\mathbb{E}}_{s_t\sim \mathcal{D}}\left[{\mathbb{D}}_{KL}\right({\pi }_{\varphi }(\cdot |s_t)|\left|\frac{\exp (Q_{\theta }(s_t,\cdot ))}{Z_{\theta }(s_t)}\right)]\\ & ={\mathbb{E}}_{s_t\sim \mathcal{D}}[\sum {\pi }_{\varphi }(\cdot |s_t)\ln (\frac{{\pi }_{\varphi }(\cdot |s_t)Z_{\theta }(s_t)}{\exp (Q_{\theta }(s_t,\cdot ))})]\\ & ={\mathbb{E}}_{s_t\sim \mathcal{D},a_t\sim {\pi }_{\varphi }}[\ln ({\pi }_{\varphi }(\cdot |s_t)+\ln (Z_{\theta }(s_t))-Q_{\theta }(s_t,\cdot )]\\ & ={\mathbb{E}}_{s_t\sim \mathcal{D},a_t\sim {\pi }_{\varphi }}[\ln ({\pi }_{\varphi }(\cdot |s_t))-Q_{\theta }(s_t,\cdot )]\end{array}\text{\hspace{1em}(1.4)}$$

最后一步是因为，分配函数$Z_{\theta }$与策略$\pi$无关，所以对梯度没有影响，所以在目标函数中可以直接忽略。

然后又引入了 reparameter的方法，

$$a_t=f_{\varphi }({ϵ}_t;s_t),ϵ\sim \mathcal{N}$$

将上式带入$(1.4)$中则有

$$J_{\pi }(\varphi )={\mathbb{E}}_{s_t\sim \mathcal{D},a_t\sim {\pi }_{\varphi }}\left[\ln \right({\pi }_{\varphi }(f_{\varphi }({ϵ}_t;s_t)|s_t\left)\right)-Q_{\theta }(s_t,f_{\varphi }({ϵ}_t;s_t))]$$

最后，只需要不断收集数据，缩小这两个损失函数，就可以得到收敛到一个解。

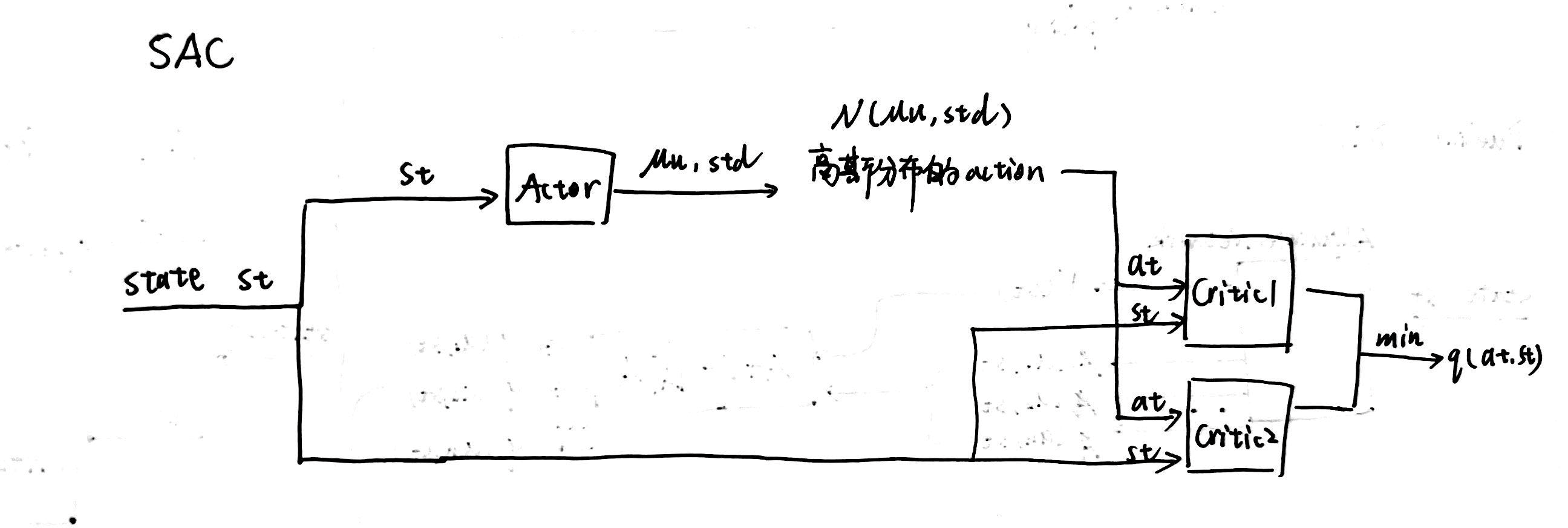
1.3 Two Q Value Neural Network

​ SAC的策略网络与DDPG中策略网络直接估计动作值大小不同，SAC的策略网络是估计连续动作空间Gaussian分布的均值和方差，再从这个Gaussian 分布中均匀采样获得连续的动作值。SAC中可以维护一个V值函数网络，也可以不维护V值函数网络，但是SAC中必须的是两个Q值函数网络及两个Q值网络的target network和一个策略网络$\pi$。为什么要维护两个Q值网络呢？这是因为为了减少Q值网络存在的过高估计的问题。然后用两个Q值网络中较小的Q值网络来计算损失函数，假设存在两个Q值网络$Q({\theta }_1),Q({\theta }_2)$和其对应的target network $Q({\theta }_1^{-}),Q({\theta }_2^{-})$

​ 那么Q值函数的损失函数就成了

$$\begin{array}{rl}{J}_Q(\theta )& ={\mathbb{E}}_{(s_t,a_t)\sim \mathcal{D}}\left[\frac{1}{2}\right(Q_{\theta }(s_t,a_t)-\hat{Q}(s_t,a_t)\left)\right]\\ \hat{Q}(s_t,a_t)& =r(s_t,a_t)+\gamma V_{\psi }(s_{t+1})\\ V_{\psi }(s_{t+1})& =Q_{\theta }(s_{t+1},a_{t+1})-\alpha \log (\pi (a_{t+1}|s_{t+1}))\end{array}\text{\hspace{1em}(1.5)(1.6)(1.7)}$$

结合式子$1.5,1.6,1.7$则有

$$J_Q(\theta )={\mathbb{E}}_{(s_t,a_t)\sim \mathcal{D}}\left[\frac{1}{2}\right(Q_{\theta }(s_t,a_t)-(r(s_t,a_t)+\gamma (\underset{j=1,2}{\min }{Q}_{{\theta }_j^{-}}(s_{t+1},a_{t+1})-\alpha \log \pi (a_{t+1}|s_{t+1}))\left){)}^2\right]$$

因为SAC也是一种离线的算法，为了让训练更加稳定，这里使用了目标Q网络$Q({\theta }^{-})$，同样是两个目标网络，与两个Q网络相对应，SAC中目标Q网络的更新方式和DDPG中一致。

​ 之前推导了策略$\pi (\varphi )$的损失函数如下

$$J_{\pi }(\varphi )={\mathbb{E}}_{s_t\sim \mathcal{D},a_t\sim {\pi }_{\varphi }}[\ln ({\pi }_{\varphi }(\cdot |s_t))-Q_{\theta }(s_t,\cdot )]$$

再引入reparameter化简之后，就成了

$$J_{\pi }(\varphi )={\mathbb{E}}_{s_t\sim \mathcal{D},a_t\sim {\pi }_{\varphi }}\left[\ln \right({\pi }_{\varphi }(f_{\varphi }({ϵ}_t;s_t)|s_t\left)\right)-Q_{\theta }(s_t,f_{\varphi }({ϵ}_t;s_t))]$$

利用双Q网络取最小，再将上述目标函数进行改写

$$J_{\pi }(\varphi )={\mathbb{E}}_{s_t\sim \mathcal{D},a_t\sim {\pi }_{\varphi }}\left[\ln \right({\pi }_{\varphi }(f_{\varphi }({ϵ}_t;s_t)|s_t\left)\right)-\underset{j=1,2}{\min }{Q}_{{\theta }_j}(s_t,f_{\varphi }({ϵ}_t;s_t))]$$

1.4 Tricks

​ SAC还集成了一些别的算法的常用技巧，比如Replay Buffer来产生independent and identically distribution的样本，使用了Double DQN中target network的思想使用两个网络。SAC中最重要的一个技巧是自动调整熵正则项，在 SAC 算法中，如何选择熵正则项的系数非常重要。在不同的状态下需要不同大小的熵：在最优动作不确定的某个状态下，熵的取值应该大一点；而在某个最优动作比较确定的状态下，熵的取值可以小一点。为了自动调整熵正则项，SAC 将强化学习的目标改写为一个带约束的优化问题：

$$\underset{\pi }{\max }{\mathbb{E}}_{\pi }[\sum _{t}r(s_t,a_t)]\text{s.t.}{\mathbb{E}}_{(s_t,a_t)\sim {\rho }_{\pi }}[-\log ({\pi }_t(a_t|s_t))]\ge {\mathcal{H}}_0$$

${\mathcal{H}}_0$ 是预先定义好的最小策略熵的阈值。通过一些数学技巧简化，可以得到温度$\alpha$的损失函数

$$J(\alpha )={\mathbb{E}}_{s_t\sim R,a_t\sim \pi (\cdot |s_t)}[-\alpha \log ({\pi }_t(a_t|s_t))-\alpha {\mathcal{H}}_0]$$

1.5 Pesudocode

2. 代码实现

2.1 SAC处理连续动作空间

采用gymnasium中Pendulum-v1的连续动作环境，整体代码如下

import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.distributions import Normalfrom tqdm import tqdm
import collections
import random
import numpy as np
import matplotlib.pyplot as plt
import gym# replay buffer
class ReplayBuffer():def __init__(self, capacity):self.buffer = collections.deque(maxlen=capacity)def add(self, s, r, a, s_, d):self.buffer.append((s,r,a,s_,d))def sample(self, batch_size):transitions = random.sample(self.buffer, batch_size)states, rewards, actions, next_states, dones = zip(*transitions)return np.array(states), rewards, actions, np.array(next_states), donesdef size(self):return len(self.buffer)# Actor
class PolicyNet_Continuous(nn.Module):"""动作空间符合高斯分布,输出动作空间的均值mu,和标准差std"""def __init__(self, state_dim, hidden_dim, action_dim, action_bound):super(PolicyNet_Continuous, self).__init__()self.fc1 = nn.Sequential(nn.Linear(in_features=state_dim, out_features=hidden_dim),nn.ReLU())self.fc_mu = nn.Linear(in_features=hidden_dim, out_features=action_dim)self.fc_std = nn.Sequential(nn.Linear(in_features=hidden_dim, out_features=action_dim),nn.Softplus())self.action_bound = action_bounddef forward(self, s):x = self.fc1(s)mu = self.fc_mu(x)std = self.fc_std(x)distribution = Normal(mu, std)normal_sample = distribution.rsample()normal_log_prob = distribution.log_prob(normal_sample)# get action limit to [-1,1]action = torch.tanh(normal_sample)# get tanh_normal log probabilitytanh_log_prob = normal_log_prob - torch.log(1 - torch.tanh(action).pow(2) + 1e-7)# get action boundedaction = action * self.action_boundreturn action, tanh_log_prob# Critic
class QValueNet_Continuous(nn.Module):def __init__(self, state_dim, hidden_dim, action_dim):super(QValueNet_Continuous, self).__init__()self.fc1 = nn.Sequential(nn.Linear(in_features=state_dim + action_dim, out_features=hidden_dim),nn.ReLU())self.fc2 = nn.Sequential(nn.Linear(in_features=hidden_dim, out_features=hidden_dim),nn.ReLU())self.fc_out = nn.Linear(in_features=hidden_dim, out_features=1)def forward(self, s, a):cat = torch.cat([s,a], dim=1)x = self.fc1(cat)x = self.fc2(x)return self.fc_out(x)# maximize entropy deep reinforcement learning SAC
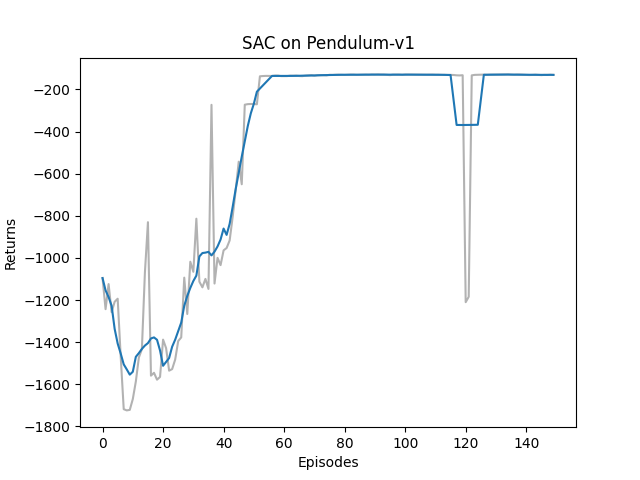
class SAC_Continuous():def __init__(self, state_dim, hidden_dim, action_dim, action_bound,actor_lr, critic_lr, alpha_lr, target_entropy, tau, gamma,device):# actorself.actor = PolicyNet_Continuous(state_dim, hidden_dim, action_dim, action_bound).to(device)# two criticsself.critic1 = QValueNet_Continuous(state_dim, hidden_dim, action_dim).to(device)self.critic2 = QValueNet_Continuous(state_dim, hidden_dim, action_dim).to(device)# two target criticsself.target_critic1 = QValueNet_Continuous(state_dim, hidden_dim, action_dim).to(device)self.target_critic2 = QValueNet_Continuous(state_dim, hidden_dim, action_dim).to(device)# initialize with same parametersself.target_critic1.load_state_dict(self.critic1.state_dict())self.target_critic2.load_state_dict(self.critic2.state_dict())# specify optimizersself.optimizer_actor = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)self.optimizer_critic1 = torch.optim.Adam(self.critic1.parameters(), lr=critic_lr)self.optimizer_critic2 = torch.optim.Adam(self.critic2.parameters(), lr=critic_lr)# 使用alpha的log值可以使训练稳定self.log_alpha = torch.tensor(np.log(0.01), dtype=torch.float, requires_grad = True)self.optimizer_log_alpha = torch.optim.Adam([self.log_alpha], lr=alpha_lr)self.target_entropy = target_entropyself.gamma = gammaself.tau = tauself.device = devicedef take_action(self, state):state = torch.tensor(np.array([state]), dtype=torch.float).to(self.device)action, _ = self.actor(state)return [action.item()]# calculate td targetdef calc_target(self, rewards, next_states, dones):next_action, log_prob = self.actor(next_states)entropy = -log_probq1_values = self.target_critic1(next_states, next_action)q2_values = self.target_critic2(next_states, next_action)next_values = torch.min(q1_values, q2_values) + self.log_alpha.exp() * entropytd_target = rewards + self.gamma * next_values * (1-dones)return td_target# soft update methoddef soft_update(self, net, target_net):for param_target, param in zip(target_net.parameters(), net.parameters()):param_target.data.copy_(param_target.data * (1.0-self.tau) + param.data * self.tau)def update(self, transition_dict):states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1,1).to(self.device)actions = torch.tensor(transition_dict['actions'], dtype=torch.float).view(-1,1).to(self.device)next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1,1).to(self.device)rewards = (rewards + 8.0) / 8.0     #对倒立摆环境的奖励进行重塑，方便训练# update two Q-value networktd_target = self.calc_target(rewards, next_states, dones).detach()critic1_loss = torch.mean(F.mse_loss(td_target, self.critic1(states, actions)))critic2_loss = torch.mean(F.mse_loss(td_target, self.critic2(states, actions)))self.optimizer_critic1.zero_grad()critic1_loss.backward()self.optimizer_critic1.step()self.optimizer_critic2.zero_grad()critic2_loss.backward()self.optimizer_critic2.step()# update policy networknew_actions, log_prob = self.actor(states)entropy = - log_probq1_value = self.critic1(states, new_actions)q2_value = self.critic2(states, new_actions)actor_loss = torch.mean(-self.log_alpha.exp() * entropy - torch.min(q1_value, q2_value))self.optimizer_actor.zero_grad()actor_loss.backward()self.optimizer_actor.step()# update temperature alphaalpha_loss = torch.mean((entropy - self.target_entropy).detach() * self.log_alpha.exp())self.optimizer_log_alpha.zero_grad()alpha_loss.backward()self.optimizer_log_alpha.step()# soft update target Q-value networkself.soft_update(self.critic1, self.target_critic1)self.soft_update(self.critic2, self.target_critic2)def train_off_policy_agent(env, agent, num_episodes, replay_buffer, minimal_size, batch_size, render, seed_number):return_list = []for i in range(10):with tqdm(total=int(num_episodes/10), desc='Iteration %d'%(i+1)) as pbar:for i_episode in range(int(num_episodes/10)):observation, _ = env.reset(seed=seed_number)done = Falseepisode_return = 0while not done:if render:env.render()action = agent.take_action(observation)observation_, reward, terminated, truncated, _ = env.step(action)done = terminated or truncatedreplay_buffer.add(observation, action, reward, observation_, done)# swap statesobservation = observation_episode_return += rewardif replay_buffer.size() > minimal_size:b_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(batch_size)transition_dict = {'states': b_s,'actions': b_a,'rewards': b_r,'next_states': b_ns,'dones': b_d}agent.update(transition_dict)return_list.append(episode_return)if(i_episode+1) % 10 == 0:pbar.set_postfix({'episode': '%d'%(num_episodes/10 * i + i_episode + 1),'return': "%.3f"%(np.mean(return_list[-10:]))})pbar.update(1)env.close()return return_listdef moving_average(a, window_size):cumulative_sum = np.cumsum(np.insert(a, 0, 0)) middle = (cumulative_sum[window_size:] - cumulative_sum[:-window_size]) / window_sizer = np.arange(1, window_size-1, 2)begin = np.cumsum(a[:window_size-1])[::2] / rend = (np.cumsum(a[:-window_size:-1])[::2] / r)[::-1]return np.concatenate((begin, middle, end))def plot_curve(return_list, mv_return, algorithm_name, env_name):episodes_list = list(range(len(return_list)))plt.plot(episodes_list, return_list, c='gray', alpha=0.6)plt.plot(episodes_list, mv_return)plt.xlabel('Episodes')plt.ylabel('Returns')plt.title('{} on {}'.format(algorithm_name, env_name))plt.show()if __name__ == "__main__":# reproducibleseed_number = 0random.seed(seed_number)np.random.seed(seed_number)torch.manual_seed(seed_number)num_episodes = 150     # episodes lengthhidden_dim = 128        # hidden layers dimensiongamma = 0.98            # discounted rateactor_lr = 1e-4         # lr of actorcritic_lr = 1e-3        # lr of criticalpha_lr = 1e-4tau = 0.005             # soft update parameterbuffer_size = 10000minimal_size = 1000batch_size = 64device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')env_name = 'Pendulum-v1'render = Falseif render:env = gym.make(id=env_name, render_mode='human')else:env = gym.make(id=env_name)state_dim = env.observation_space.shape[0]action_dim = env.action_space.shape[0]  action_bound = env.action_space.high[0]# entropy初始化为动作空间维度的负数target_entropy = - env.action_space.shape[0]replaybuffer = ReplayBuffer(buffer_size)agent = SAC_Continuous(state_dim, hidden_dim, action_dim, action_bound, actor_lr, critic_lr, alpha_lr, target_entropy, tau, gamma, device)return_list = train_off_policy_agent(env, agent, num_episodes, replaybuffer, minimal_size, batch_size, render, seed_number)mv_return = moving_average(return_list, 9)plot_curve(return_list, mv_return, 'SAC', env_name)

所获得的回报曲线如下图

2.2 SAC处理离散动作空间

采用gaymnasium中的CartPole-v1离散动作空间的环境。

import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.distributions import Categoricalfrom tqdm import tqdm
import collections
import random
import numpy as np
import matplotlib.pyplot as plt
import gym# replay buffer
class ReplayBuffer():def __init__(self, capacity):self.buffer = collections.deque(maxlen=capacity)def add(self, s, r, a, s_, d):self.buffer.append((s,r,a,s_,d))def sample(self, batch_size):transitions = random.sample(self.buffer, batch_size)states, rewards, actions, next_states, dones = zip(*transitions)return np.array(states), rewards, actions, np.array(next_states), donesdef size(self):return len(self.buffer)# Actor
class PolicyNet_Discrete(nn.Module):"""动作空间服从离散的概率分布,输出每个动作的概率值"""def __init__(self, state_dim, hidden_dim, action_dim):super(PolicyNet_Discrete, self).__init__()self.fc1 = nn.Sequential(nn.Linear(in_features=state_dim, out_features=hidden_dim),nn.ReLU())self.fc2 = nn.Sequential(nn.Linear(in_features=hidden_dim, out_features=action_dim),nn.Softmax(dim=1))def forward(self, s):x = self.fc1(s)return self.fc2(x)# Critic
class QValueNet_Discrete(nn.Module):def __init__(self, state_dim, hidden_dim, action_dim):super(QValueNet_Discrete, self).__init__()self.fc1 = nn.Sequential(nn.Linear(in_features=state_dim, out_features=hidden_dim),nn.ReLU())self.fc2 = nn.Linear(in_features=hidden_dim, out_features=action_dim)def forward(self, s):x = self.fc1(s)return self.fc2(x)# maximize entropy deep reinforcement learning SAC
class SAC_Continuous():def __init__(self, state_dim, hidden_dim, action_dim,actor_lr, critic_lr, alpha_lr, target_entropy, tau, gamma,device):# actorself.actor = PolicyNet_Discrete(state_dim, hidden_dim, action_dim).to(device)# two criticsself.critic1 = QValueNet_Discrete(state_dim, hidden_dim, action_dim).to(device)self.critic2 = QValueNet_Discrete(state_dim, hidden_dim, action_dim).to(device)# two target criticsself.target_critic1 = QValueNet_Discrete(state_dim, hidden_dim, action_dim).to(device)self.target_critic2 = QValueNet_Discrete(state_dim, hidden_dim, action_dim).to(device)# initialize with same parametersself.target_critic1.load_state_dict(self.critic1.state_dict())self.target_critic2.load_state_dict(self.critic2.state_dict())# specify optimizersself.optimizer_actor = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)self.optimizer_critic1 = torch.optim.Adam(self.critic1.parameters(), lr=critic_lr)self.optimizer_critic2 = torch.optim.Adam(self.critic2.parameters(), lr=critic_lr)# 使用alpha的log值可以使训练稳定self.log_alpha = torch.tensor(np.log(0.01), dtype=torch.float, requires_grad = True)self.optimizer_log_alpha = torch.optim.Adam([self.log_alpha], lr=alpha_lr)self.target_entropy = target_entropyself.gamma = gammaself.tau = tauself.device = devicedef take_action(self, state):state = torch.tensor(np.array([state]), dtype=torch.float).to(self.device)probs = self.actor(state)action_dist = Categorical(probs)action = action_dist.sample()return action.item()# calculate td targetdef calc_target(self, rewards, next_states, dones):next_probs = self.actor(next_states)next_log_probs = torch.log(next_probs + 1e-8)entropy = -torch.sum(next_probs * next_log_probs, dim=1, keepdim=True)q1_values = self.target_critic1(next_states)q2_values = self.target_critic2(next_states)min_qvalue = torch.sum(next_probs * torch.min(q1_values, q2_values),dim=1,keepdim=True)next_value = min_qvalue + self.log_alpha.exp() * entropytd_target = rewards + self.gamma * next_value * (1 - dones)return td_target# soft update methoddef soft_update(self, net, target_net):for param_target, param in zip(target_net.parameters(), net.parameters()):param_target.data.copy_(param_target.data * (1.0-self.tau) + param.data * self.tau)def update(self, transition_dict):states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1,1).to(self.device)actions = torch.tensor(transition_dict['actions'], dtype=torch.int64).view(-1,1).to(self.device)next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1,1).to(self.device)rewards = (rewards + 8.0) / 8.0     #对倒立摆环境的奖励进行重塑，方便训练# update two Q-value networktd_target = self.calc_target(rewards, next_states, dones).detach()critic1_loss = torch.mean(F.mse_loss(td_target, self.critic1(states).gather(dim=1,index=actions)))critic2_loss = torch.mean(F.mse_loss(td_target, self.critic2(states).gather(dim=1,index=actions)))self.optimizer_critic1.zero_grad()critic1_loss.backward()self.optimizer_critic1.step()self.optimizer_critic2.zero_grad()critic2_loss.backward()self.optimizer_critic2.step()# update policy networkprobs = self.actor(states)log_probs = torch.log(probs + 1e-8)entropy = -torch.sum(probs * log_probs, dim=1, keepdim=True)q1_value = self.critic1(states)q2_value = self.critic2(states)min_qvalue = torch.sum(probs * torch.min(q1_value, q2_value),dim=1,keepdim=True)  # 直接根据概率计算期望actor_loss = torch.mean(-self.log_alpha.exp() * entropy - min_qvalue)self.optimizer_actor.zero_grad()actor_loss.backward()self.optimizer_actor.step()# update temperature alphaalpha_loss = torch.mean((entropy - self.target_entropy).detach() * self.log_alpha.exp())self.optimizer_log_alpha.zero_grad()alpha_loss.backward()self.optimizer_log_alpha.step()# soft update target Q-value networkself.soft_update(self.critic1, self.target_critic1)self.soft_update(self.critic2, self.target_critic2)def train_off_policy_agent(env, agent, num_episodes, replay_buffer, minimal_size, batch_size, render, seed_number):return_list = []for i in range(10):with tqdm(total=int(num_episodes/10), desc='Iteration %d'%(i+1)) as pbar:for i_episode in range(int(num_episodes/10)):observation, _ = env.reset(seed=seed_number)done = Falseepisode_return = 0while not done:if render:env.render()action = agent.take_action(observation)observation_, reward, terminated, truncated, _ = env.step(action)done = terminated or truncatedreplay_buffer.add(observation, action, reward, observation_, done)# swap statesobservation = observation_episode_return += rewardif replay_buffer.size() > minimal_size:b_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(batch_size)transition_dict = {'states': b_s,'actions': b_a,'rewards': b_r,'next_states': b_ns,'dones': b_d}agent.update(transition_dict)return_list.append(episode_return)if(i_episode+1) % 10 == 0:pbar.set_postfix({'episode': '%d'%(num_episodes/10 * i + i_episode + 1),'return': "%.3f"%(np.mean(return_list[-10:]))})pbar.update(1)env.close()return return_listdef moving_average(a, window_size):cumulative_sum = np.cumsum(np.insert(a, 0, 0)) middle = (cumulative_sum[window_size:] - cumulative_sum[:-window_size]) / window_sizer = np.arange(1, window_size-1, 2)begin = np.cumsum(a[:window_size-1])[::2] / rend = (np.cumsum(a[:-window_size:-1])[::2] / r)[::-1]return np.concatenate((begin, middle, end))def plot_curve(return_list, mv_return, algorithm_name, env_name):episodes_list = list(range(len(return_list)))plt.plot(episodes_list, return_list, c='gray', alpha=0.6)plt.plot(episodes_list, mv_return)plt.xlabel('Episodes')plt.ylabel('Returns')plt.title('{} on {}'.format(algorithm_name, env_name))plt.show()if __name__ == "__main__":# reproducibleseed_number = 0random.seed(seed_number)np.random.seed(seed_number)torch.manual_seed(seed_number)num_episodes = 200    # episodes lengthhidden_dim = 128        # hidden layers dimensiongamma = 0.98            # discounted rateactor_lr = 1e-3         # lr of actorcritic_lr = 1e-2        # lr of criticalpha_lr = 1e-2tau = 0.005             # soft update parameterbuffer_size = 10000minimal_size = 500batch_size = 64device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')env_name = 'CartPole-v1'render = Falseif render:env = gym.make(id=env_name, render_mode='human')else:env = gym.make(id=env_name)state_dim = env.observation_space.shape[0]action_dim = env.action_space.n  # entropy初始化为-1target_entropy = -1replaybuffer = ReplayBuffer(buffer_size)agent = SAC_Continuous(state_dim, hidden_dim, action_dim, actor_lr, critic_lr, alpha_lr, target_entropy, tau, gamma, device)return_list = train_off_policy_agent(env, agent, num_episodes, replaybuffer, minimal_size, batch_size, render, seed_number)mv_return = moving_average(return_list, 9)plot_curve(return_list, mv_return, 'SAC', env_name)

Reference

Hands on RL

SAC(Soft Actor-Critic)阅读笔记

Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor