视觉slam十四讲---第一弹三维空间刚体运动
1.旋转矩阵
1.1内积

1.2外积

1.3坐标系间的欧式变换
相机运动是一个刚体运动,它保证了同一个向量在各个坐标系下的长度和夹角都不会 发生变化。这种变换称为欧氏变换。
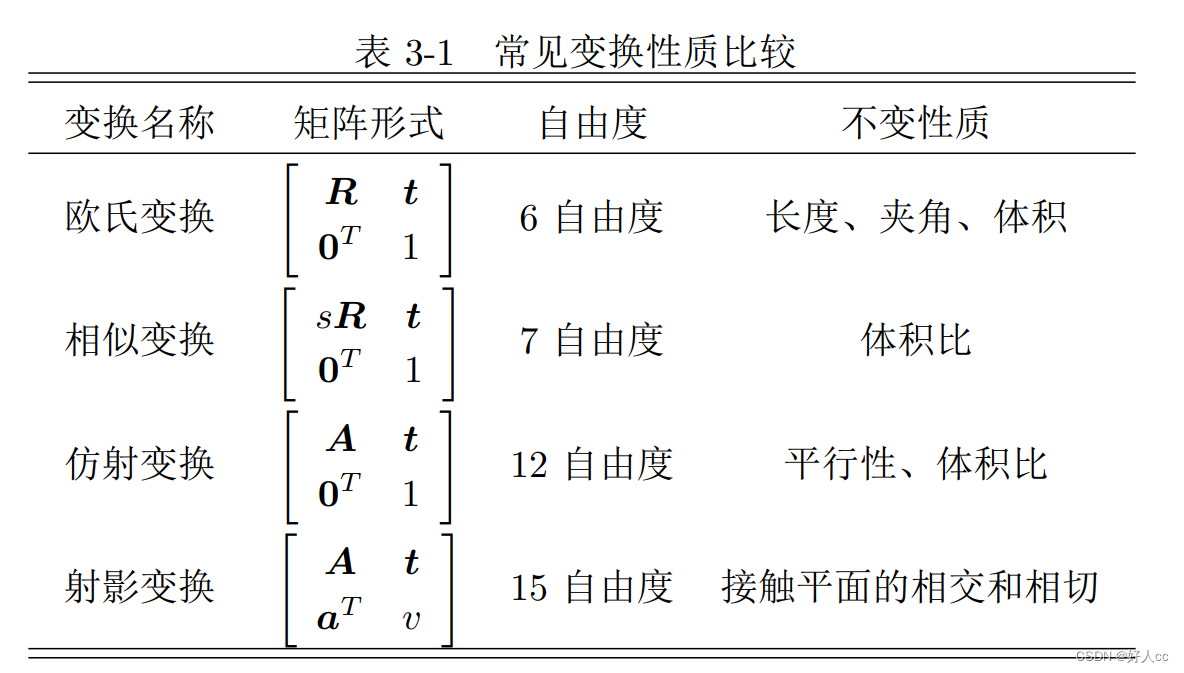
旋转矩阵:它是一个行列式为 1 的正交矩阵。

旋转矩阵为正交阵,它的逆(即转置)描述了一个相反的旋转。
加上平移:

1.4变换矩阵与齐次坐标

关于变换矩阵 T,它具有比较特别的结构:左上角为旋转矩阵,右侧为平移向量,左 下角为 0 向量,右下角为 1。这种矩阵又称为特殊欧氏群(Special Euclidean Group):
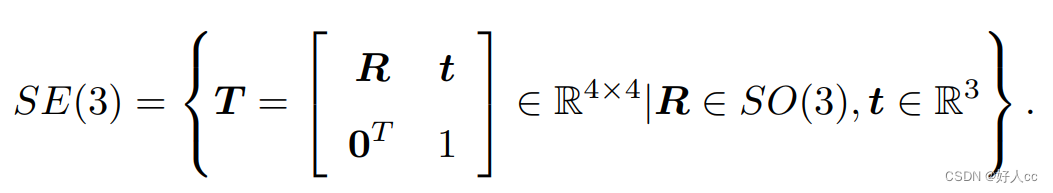
求解该矩阵的逆表示一个反向的变换:
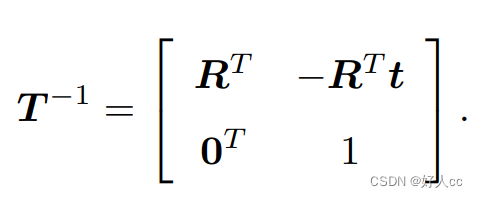
2.Eigen库---线性代数库
#include <Eigen/Core> //核心部分
#include <Eigen/Dense> //稠密矩阵的代数运算(逆、特征值等)
using namespace Eigen;
//所有的向量,矩阵都是
Matrix<数据类型,行,列>
Vector3d实质是 Matrix<double,3,1>
可以直接求逆 QR分解 cholesky分解Eigen对数据类型转换严格,可以通过显示转换来完成转换。
3.旋转向量和欧拉角
3.1旋转向量
事实上, 任意旋转都可以用一个旋转轴和一个旋转角来刻画。
于是,我们可以使用一个 向量,其方向与旋转轴一致,而长度等于旋转角。这种向量,称为旋转向量(或轴角,AxisAngle)。这种表示法只需一个三维向量即可描述旋转。同样,对于变换矩阵,我们使用一 个旋转向量和一个平移向量即可表达一次变换。这时的维数正好是六维。
旋转向量和旋转矩阵 之间是如何转换的呢?假设有一个旋转轴为 n,角度为 θ 的旋转,显然,它对应的旋转向 量为 θn。由旋转向量到旋转矩阵的过程由罗德里格斯公式
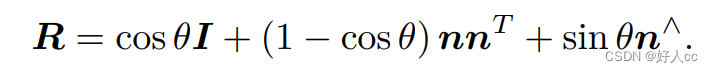
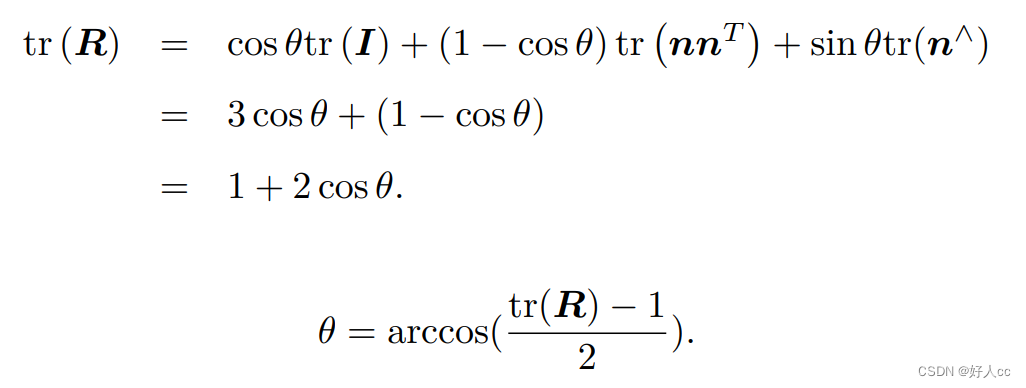

3.2欧拉角

欧拉角的一个重大缺点是会碰到著名的万向锁问题(Gimbal Lock①):在俯仰角为 ±90◦ 时,第一次旋转与第三次旋转将使用同一个轴,使得系统丢失了一个自由度(由三次 旋转变成了两次旋转)。这被称为奇异性问题,在其他形式的欧拉角中也同样存在。
4.四元数
既是紧凑的,也没有奇异性。如果说缺点的话,四元数不够直观,其运算稍为复杂一些。



这式子给我们一种微妙的“转了一半”的感觉。同样,对式(3.19)的 θ 加上 2π,我们得到一个相同的旋转,但此时对应的四元数变成了 −q。因此,在四元数中,任意的旋转都可以由两个互为相反数的四元数表示。
四元数和自己的逆的乘积为实四元数的 1:

5.四元数到旋转矩阵的转换

6.变换性质