图解LeetCode——剑指 Offer 10- II. 青蛙跳台阶问题
一、题目
一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
二、示例
2.1> 示例 1:
【输入】n = 2
【输出】2
2.2> 示例 2:
【输入】n = 7
【输出】21
2.3> 示例 3:
【输入】n = 0
【输出】1
提示:
0<= n <=100
三、解题思路
根据题目描述,青蛙只能跳1级台阶或者跳2级台阶,那么我们可以针对这个条件,演示一下不同台阶青蛙的跳法。比如:
- 对于1阶台阶来说,小青蛙只有1种跳法,就是向上跳1级;
- 对于2阶台阶来说,小青蛙有2种跳法,分别是:向上跳1级然后再跳1级 & 直接向上跳2级;
- 对于3阶台阶来说,小青蛙有3种跳法,分别是:执行3次1级跳 & 直接向上跳2级再跳1级 & 先跳1级然后直接向上跳2级;
- 对于4阶台阶来说,小青蛙有5种跳法,分别是:执行4次1级跳 & 2次1级跳再直接跳2级 & 直接跳2级再执行2次1级跳 & 1级跳再直接跳2级再执行1次1级跳 & 执行2次2极跳;
- ……
针对上面描述,我们来看下面图示,会更好理解一些:
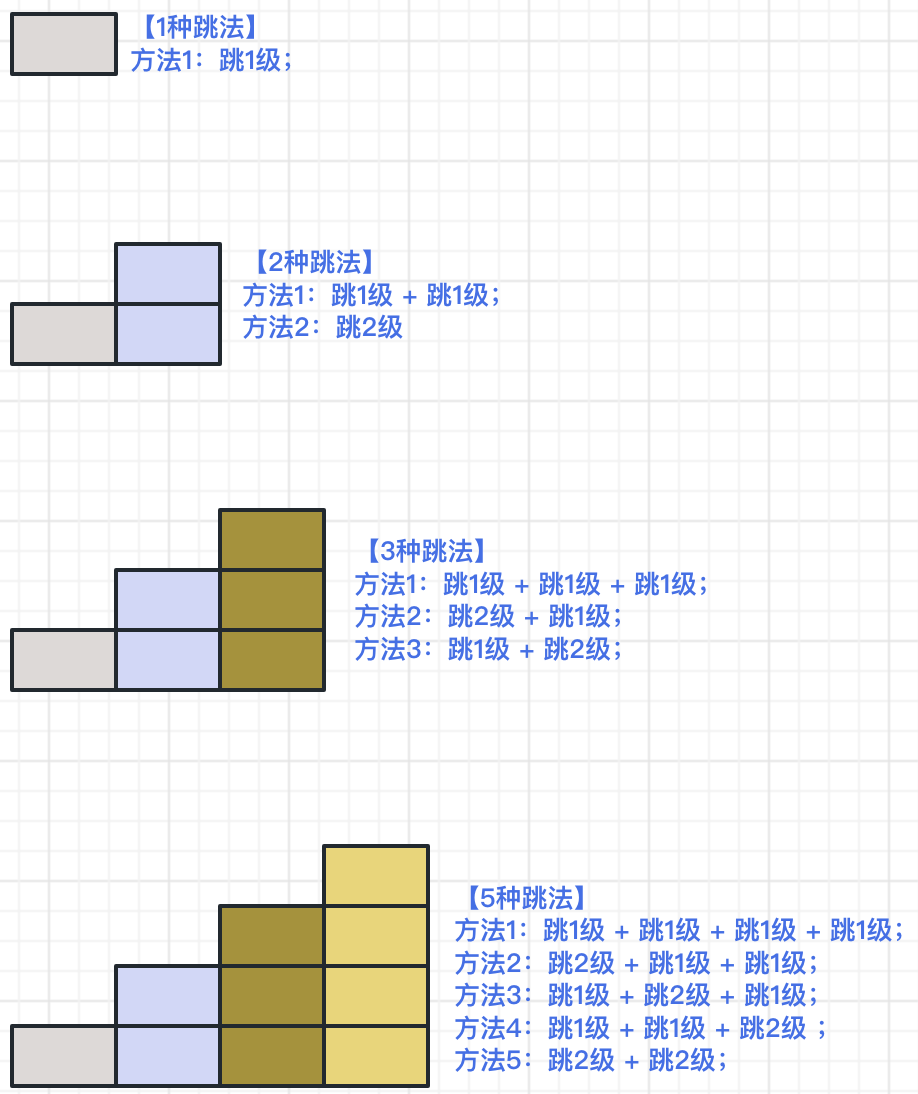
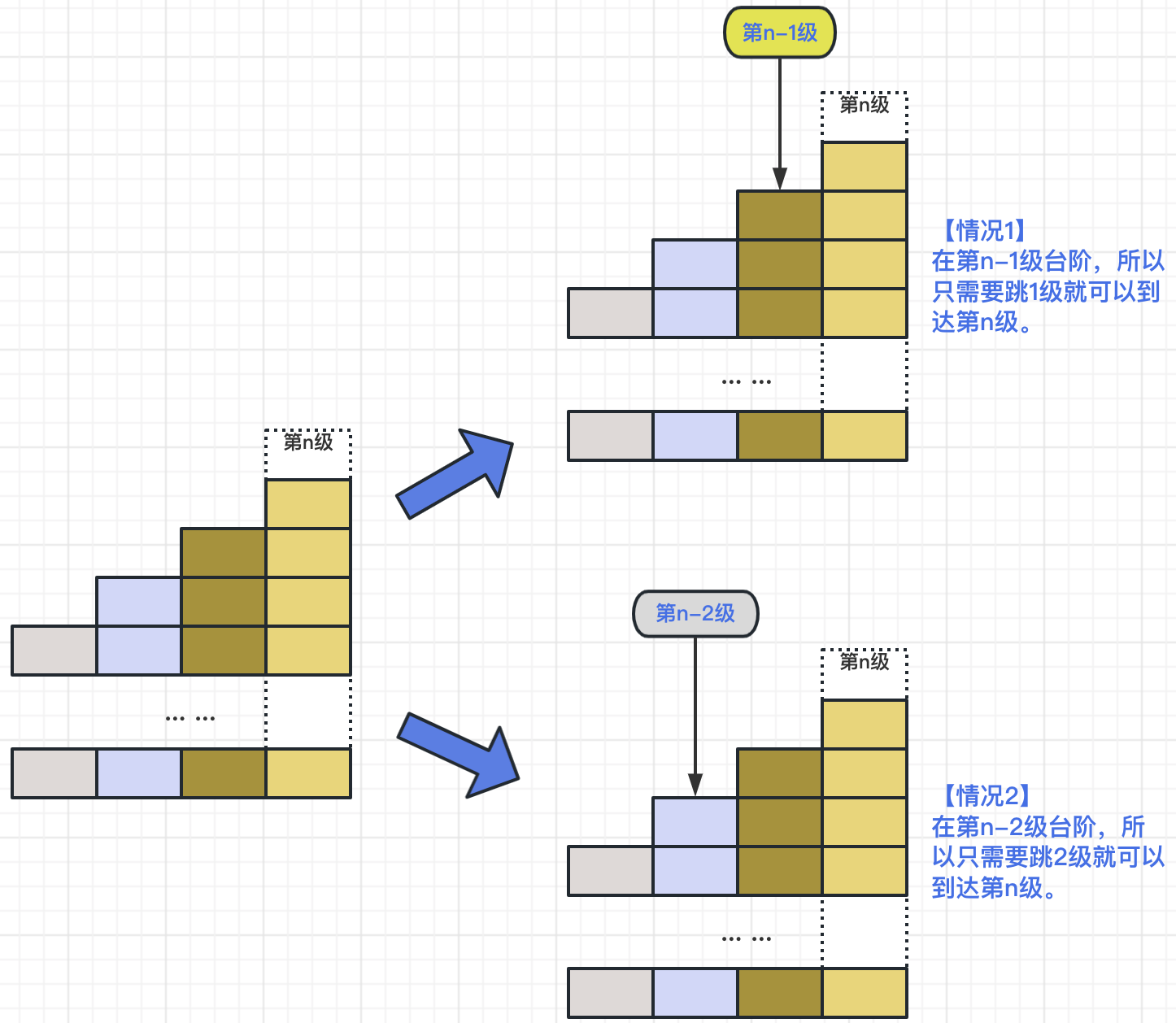
从上面的示例中,我们可以看到从1阶到4阶的跳法分别是:1种、2种、3种、5种……,是不是似曾相识呢?是的,就是斐波那契数列!那为什么会是这样的规律呢?下面我们以第n级台阶来看,对于它来说,往前一步其实只有两种情况:
【情况1】在第
n-1级处,那么只需要向上跳1步即可。
【情况2】在第n-2级处,那么只需要向上跳2步即可。
既然是这样,我们以f(n)表示到达第n级阶梯的跳法,那么可以推理出 f(n) = f(n-1) + f(n-2) , 所以,我们根据推导出的公式关系,就可以解出——青蛙跳上一个 n 级的台阶总共有多少种跳法了。
四、代码实现
class Solution {public int numWays(int n) {int a = 1, b = a, c = b, mod = (int)1e9 + 7;for (int i = 2; i <= n; i++, a = b, b = c) c = (a + b) % mod;return c;}
}
今天的文章内容就这些了:
写作不易,笔者几个小时甚至数天完成的一篇文章,只愿换来您几秒钟的 点赞 & 分享 。
更多技术干货,欢迎大家关注公众号“爪哇缪斯” ~ \(^o^)/ ~ 「干货分享,每天更新」
