数学建模(三)整数规划
视频推荐:B站_数学建模老哥
一、整数规划基本原理
数学规划中的变量(部分或全部)限制为整数时,称为整数规划。若在线性规划模型中,变量限制为整数,则称为整数线性规划。目前所流行的求解整数规划的方法,往往只适用于整数线性规划。目前还没有一种方法能有效地求解一切整数规划。
1.1 整数规划的分类
(1)变量全限制为整数时,称为纯(完全)整数规划。
(2)变量部分限制为整数的,称为混合整数规划。
(3)变量取值要么为0要么为1,称为0-1规划。
1.2 整数规划的特点
1. 原线性规划有最优解,当自变量限制为整数后,其整数规划解出现下述情况:
(1)原线性规划最优解全是整数,则整数规划最优解与线性规划最优解一致。
(2)整数规划可能不存在可行解。
(3)有可行解(当然就存在最优解),但最优解值变差。
2. 整数规划最优解不能按照实数最优解简单取整而获得。
1.3 案例
合理下料问题:
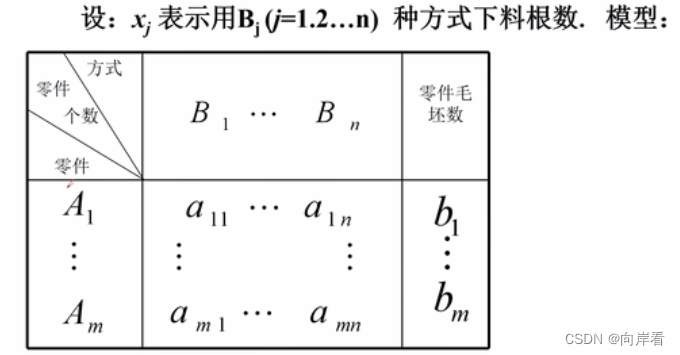
设用某型号的圆钢下零件A1,A2...,Am的毛坯。在一根圆钢上下料的方式有B1,B2,... Bn种,每种下料方式可以得到各种零件的毛坯数以及每种零件的需要量,如表所示。问怎样安排下料方式,使得即满足需要,所用的原材料又最少?
如表所示:
模型:
其中,xj表示用Bj种方式下料根数,aij为每种下料方式可以得到各种零件的毛坯数,bi每种零件的需要量。
1.4 整数规划的数学模型一般形式
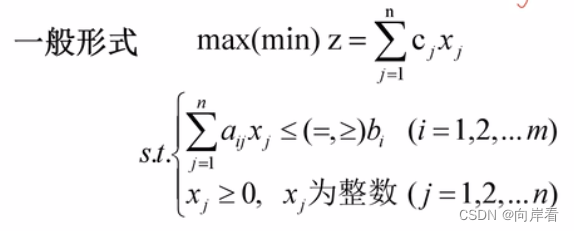
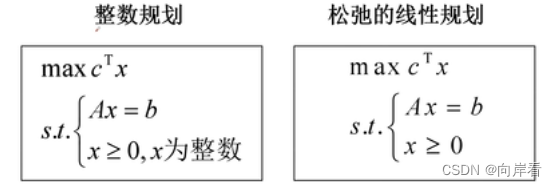
另外补充: 整数规划与松弛的线性规划之间的关系。
不难看出两者之间的关系。
二、整数线性规划的求解方法
从数学模型上看整数规划似乎是线性规划的一种特殊形式,求解只需在线性规划的基础上,通过舍入取整,寻求满足整数要求的解即可。但实际上两者却有很大的不同,通过舍入得到的解(整数)也不一定就是最优解,有时甚至不能保证所得到的解是整数可行解。
2.1 分枝定界法
1. 先求出相应松弛问题的最优解。
2. 若松弛问题无可行解,则整数线性规划问题无可行解。
3. 若求得的松弛问题最优解符合整数要求,则是整数线性规划问题的最优解。若不满足整数条件,则任选一个不满足整数条件的变量 来构造新的约束,分别添加到松弛问题中形成两个子问题:
和
依次在缩小的可行域中求解新构造的线性规划的最优解,并重复上述过程,直到子问题无解或有整数最优解(被查清)。
Q:为什么在步骤3中不满足整数条件时要添加上述两个约束条件?
A:因为变量
是一个不满足整数条件的变量,它注定无法构成整数规划的最优解,因此我们要向变量
的两边去寻找合适的整数最优解。
注意:构造新的约束条件是分别到整数规划问题对应的松弛问题中,独立构成两个不同的子问题再求解。
详情参考:分枝定界法
案例:分枝定界法总体上有点像二叉树,能看懂下面的案例基本就能理解分枝定界法。