数据结构【图的类型定义和存储结构】
数据结构之图
- 图的定义和概念
- 图的定义
- 图的术语
- 图的类型定义
- 图的存储结构
- 数组(邻接矩阵)表示法
- 无向图的邻接矩阵表示法
- 有向图的邻接矩阵表示法
- 网(即有权图)的邻接矩阵表示法
- 邻接矩阵的ADT定义
- 邻接表(链式)表示法
- 无向图
- 有向图
- 图的邻接表存储表示
- 邻接表操作
- 邻接表表示无向网
图的定义和概念
图的定义
图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E)。
其中,G表示一个图,V 是图 G 中顶点的有穷非空集合,E 是图 G 中边的有穷集合。
图形结构是多对多的关系。
无向图:每条边都是无方向的。
有向图:每条边都是有方向的。
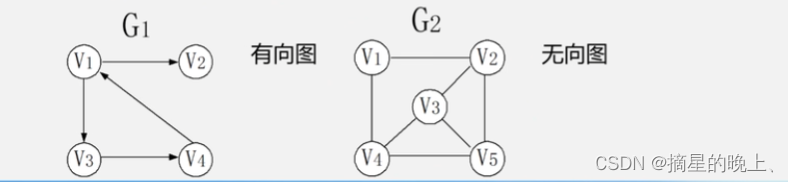
特殊:
当线性表没有数据节点时,线性表为空表。 树中没有节点时,树为空树。
但是,在图中不允许没有顶点,但是可以没有边。
完全图:任意两个点都有一条边相连。
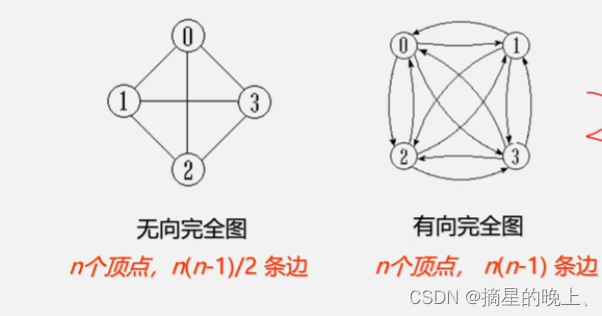
稀疏图:有很少边或弧的图(e<nlogn)。
稠密图:有较多边或弧的图。
图的术语
网:边/弧带权的图
邻接:
有边/弧相连的两个顶点之间的关系。
存在(Vi,Vj),则称Vi和Vj互为邻接点;
存在<Vi,Vj>,则称Vi邻接到Vj;, Vj邻接于Vi。
关联/依附:边/弧与顶点之间的关系。
顶点的度:
与该顶点相关联的边的数目,记为TD(v)。
在有向图中,顶点的度等于该顶点的入度与出度之和。
顶点 v 的入度是以 v 为终点的有向边的条数记作ID(v)。
顶点 v 的出度是以 v 为始点的有向边的条数记作 OD(v)。
有向图中顶点的度 = 入度 + 出度。
即 TD(V) = ID(V) + OD(V)。
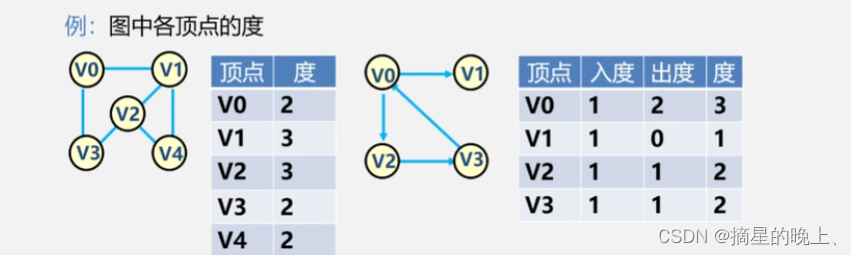
路径:接续的边构成的顶点序列。
路径长度: 路径上边或弧的数目/权值之和。
回路(环): 第一个顶点和最后一个顶点相同的路径。
简单路径: 除路径起点和终点可以相同外,其余顶点均不相同的路径。
简单回路(简单环): 除路径起点和终点相同外,其余顶点均不相同的路径。
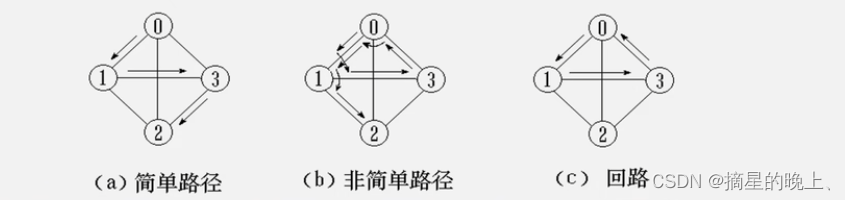
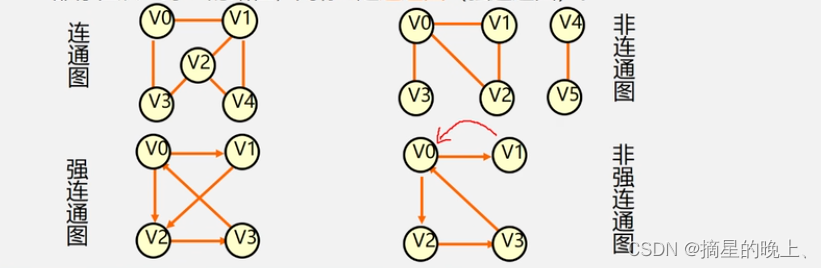
连通图:在无 (有) 向图G=( V, E) )中,若对任何两个顶点 v、u都存在从v 到 u 的路径,则称G是连通图 (强连通图)
权与网:
图中边或弧所具有的相关数称为权。表明从一个顶点到另一个顶点的距离或耗费。
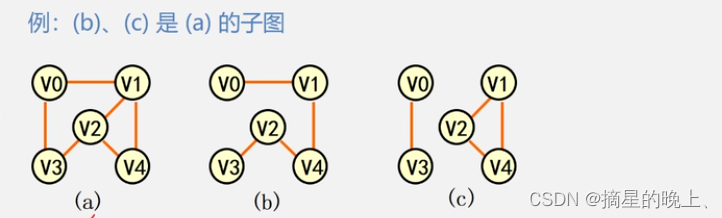
子图:
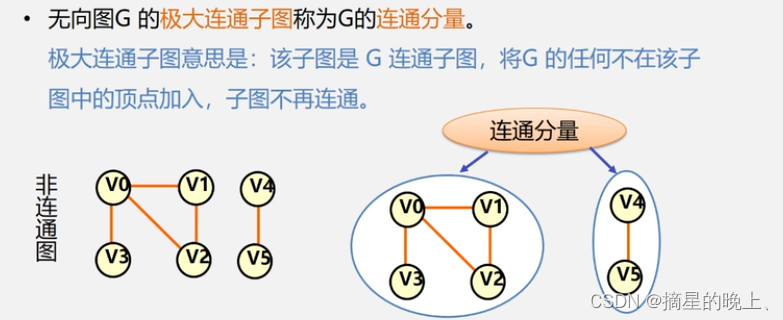
连通分量(强连通分量):
无向图中的连通分量:
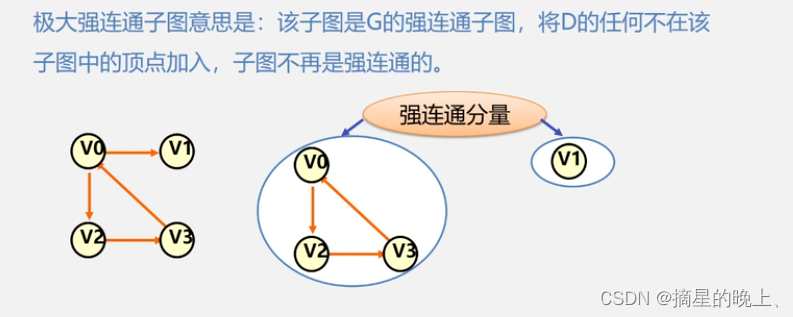
有向图中的强连通分量:
有向图G中的极大强连通子图称为G的强连通分量。
极小连通子图:
该子图是G的连通子图,在该子图中删除任何一条连通路径,子图不再连通。
生成树:包含无向图G的所有定点的极小连通子图。
生成森林:对非连通图,由各个连通分量的生成树的集合。

图的类型定义

基本操作P:
Create_Graph(&G,V,VR) : 图的创建操作
初始条件:无。
操作结果: 生成一个没有顶点的空图G。
GetVex(G,v) : 求图中的顶点v的值
初始条件: 图G存在,v是图中的一个顶点。
操作结果: 生成一个没有顶点的空图G
CreateGraph(&G,V,VR)
初始条件: V是图的顶点集,VR是图中弧的集合
操作结果: 按V和VR的定义 构造图G
DFSTraverse(G)
初始条件:图G存在
操作结果:对图进行深度优先遍历
BFSTraverse(G)
初始条件:图G存在
操作结果: 对图进行广度优先遍历
图的存储结构
图的逻辑结构:多对多
图没有顺序存储结构,但是可以用二维数组来表示元素间的关系。
链式存储结构:有数组表示法和邻接表(多重链表)表示法
数组(邻接矩阵)表示法
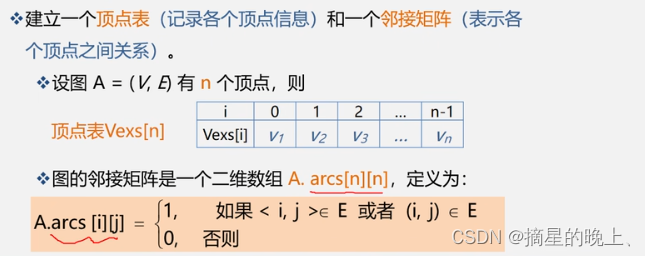
邻接矩阵的好处:
- 直观、简单、好理解 方便检查任意一对顶点间是否存在边
- 方便找任一顶点的所有“邻接点”(有边直接相连的顶点)
- 方便计算任一顶点的“度”(从该点发出的边数为“出度”,指向该点的边数为“入度”)
– 无向图:对应行(或列)非0元素的个数
– 有向图:对应行非0元素的个数是“出度”,对应列非0元素的个数是“入度
无向图的邻接矩阵表示法

完全图的邻接矩阵中,对角元素为0,其余1。
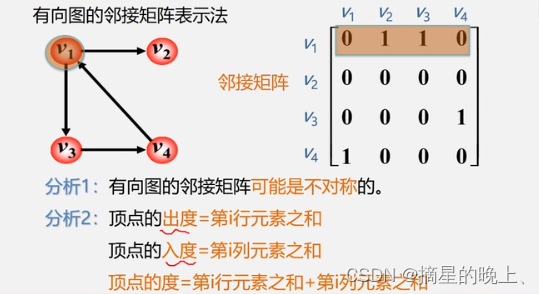
有向图的邻接矩阵表示法
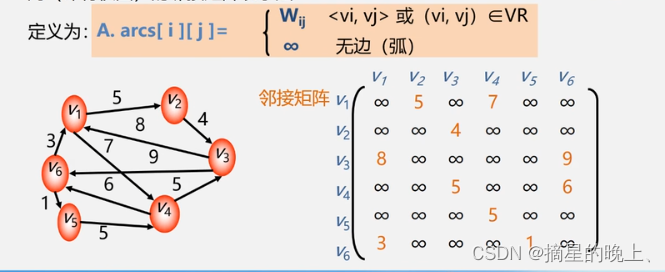
网(即有权图)的邻接矩阵表示法
邻接矩阵的ADT定义

用邻接矩阵表示法创建无向网



在图中查找顶点:
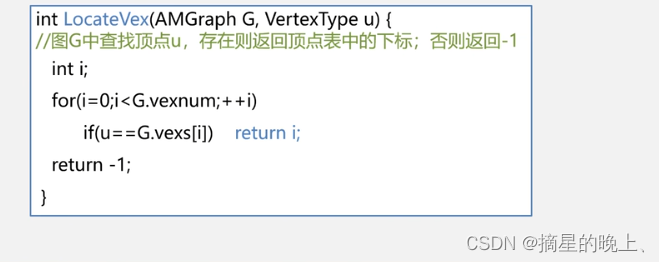
邻接表(链式)表示法
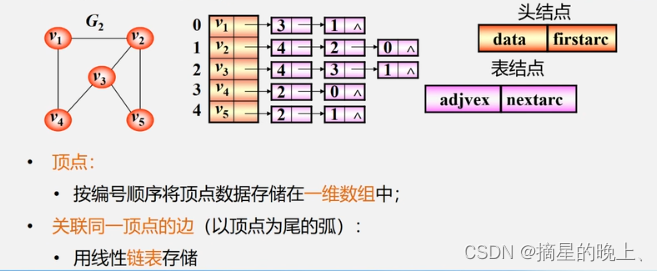
无向图
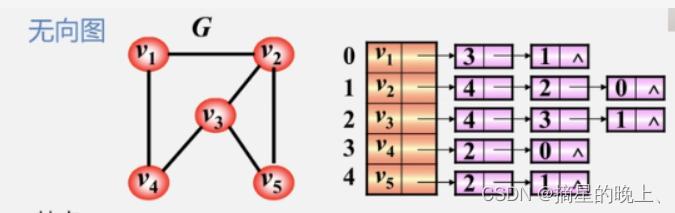
特点:
- 邻接表不唯一
- 若无向图中有 n 个顶点、e 条边,则其邻接表需 n 个头结点和2e 个表结点。适宜存储稀疏图。
- 无向图中顶点v的度为第i个单链表中的结点数。
有向图
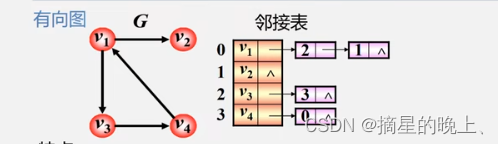
特点:
- 找出度易,找入度难。
- 顶点 v 的出度为第i个单链表中的结点个数。
- 顶点 v 的入度为整个单链表中邻接点域值是i-1的结点个数。
逆邻接表则相反
图的邻接表存储表示



邻接表操作
ALGraghG; //定义了邻接表表示的图G
G.vexum=5; G.arcnum=5; //图G包含5个顶点,5条边
G.vertices[1].data= 'b' //图G中第2个顶点是b
p=G.vertices[1].firtarc; //指针p指向顶点b的第一条边结点
p->adjvex =4; //p指针所指边结点是到下标为4的结点的边
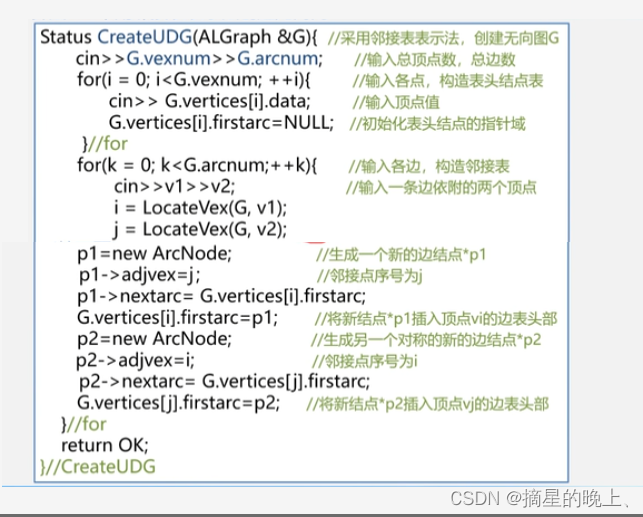
邻接表表示无向网
(1)输入总顶点数和总边数
(2)建立顶点表,依次输入点的信息存入顶点表中,使每个表头结点的指针域初始化为NULL
(3)创建邻接表,依次输入每条边依附的两个顶点,确定两个顶点的序号和,建立边结点,将此边结点分别插入到vi和vj对应的两个边链表的头部
参考资料:数据结构与算法基础-王卓老师
