想要精通算法和SQL的成长之路 - 柱状图中最大的矩形
想要精通算法和SQL的成长之路 - 柱状图中最大的矩形
- 前言
- 一. 柱状图中最大的矩形
前言
想要精通算法和SQL的成长之路 - 系列导航
一. 柱状图中最大的矩形
原题链接
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。求在该柱状图中,能够勾勒出来的矩形的最大面积。
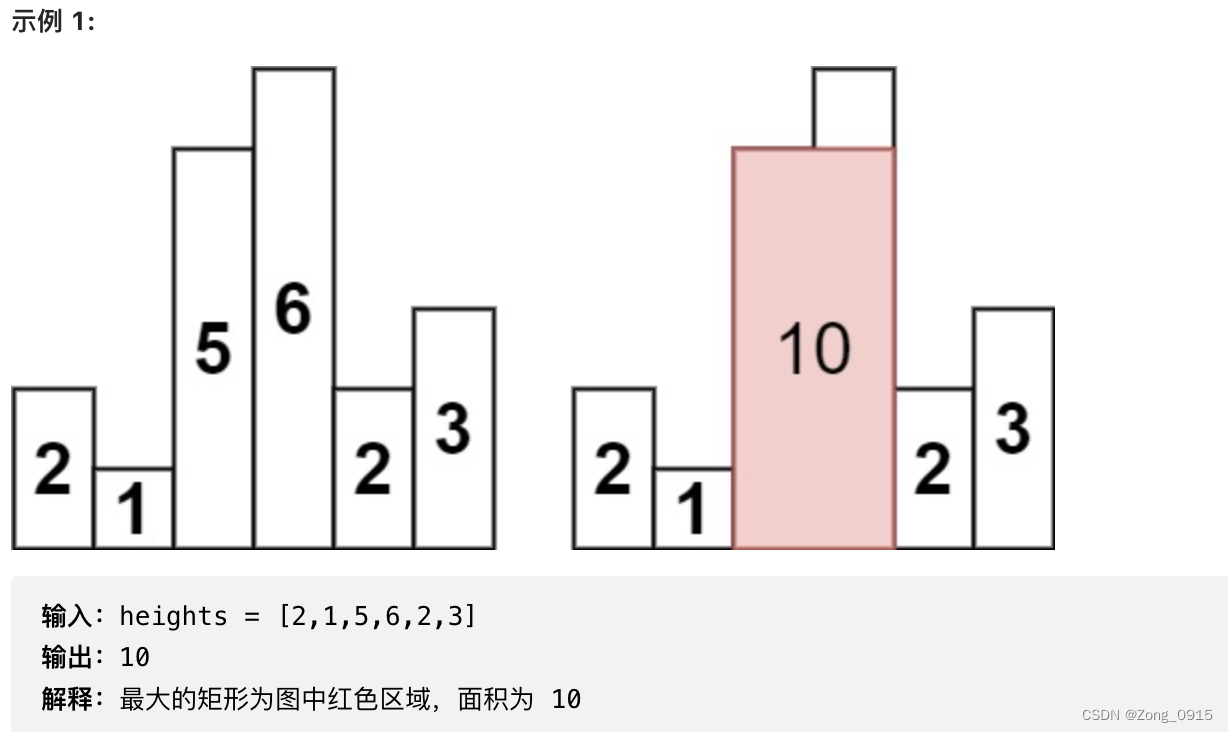
这道题目我们可以仿照着接雨水这道题目来做。
思路:
- 我们可以遍历所有的柱子,在每次遍历的时候,我们以当前柱子作为一个中心点。
- 我们分别向左、向右各自寻找第一个小于当前高度的柱子,找到他们的索引分别是
left和right。 - 那么以当前柱子为固定高度的最大面积就是 :
(right-left-1)* curHeight。
那么我们来看下题目给的案例,按按照这个思想来做是否可行呢?当我们以第一根柱子作为中心,向两侧寻找第一个最低点的时候,就出问题啦:
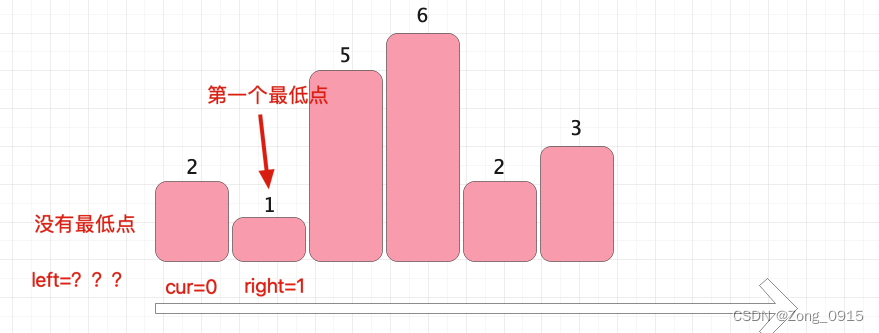
那好,我们对此情况,我们稍微改造改造,我们给数组两侧添加两个虚拟节点,高度是0,如图:
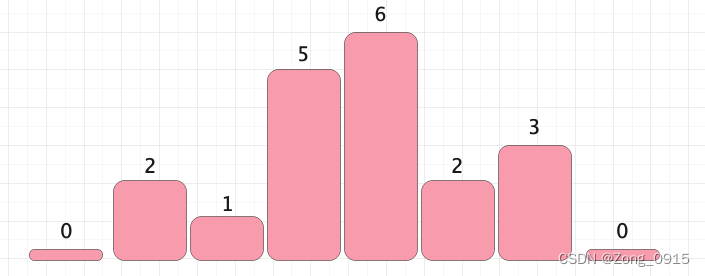
那么这样的话,left=0,cur=1,right=2。以高度为2去寻找最大面积的话,就是2*(2-0-1)=2了。
我们再来看下以柱子高度5的为中心:
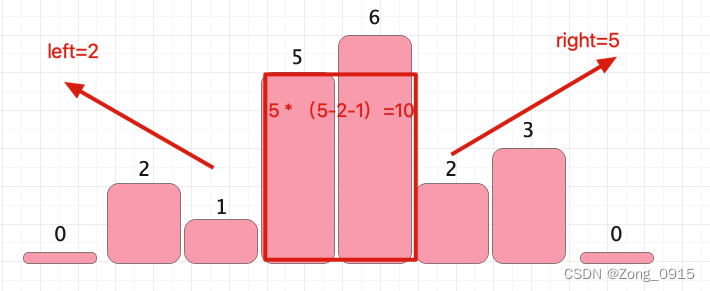
我们在试想一下,既然我们要以每个遍历的节点为中心,并寻找到左右两侧第一个比他小的元素。那么我们就可以使用单调递增栈来完成。
前期准备部分,我们先给数组添加两个虚拟节点
int[] tmpHeight = new int[heights.length + 2];
for (int i = 1; i <= heights.length; i++) {tmpHeight[i] = heights[i - 1];
}
然后我们再看看递归过程:
- 既然我们需要单调递增,那么遇到小的,就应该把当前栈内比当前高度高的,给剔除(同时计算高度)。也就保证了循环:
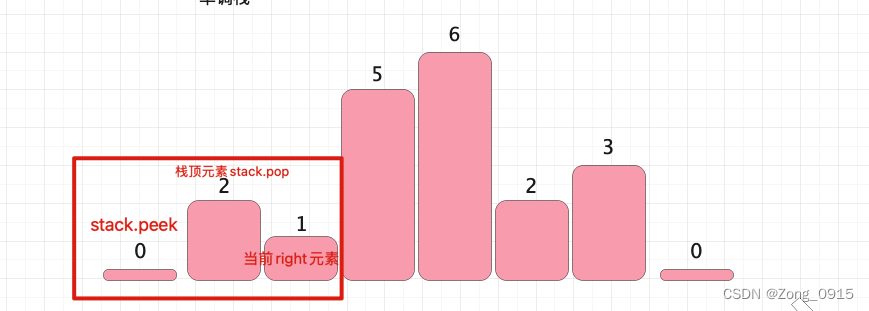
while (!stack.isEmpty()&&tmpHeight[stack.peek()]>tmpHeight[right])。因为无论怎么样,我们必须要把当前元素给放到栈中的。不能不放。 - 既然是单调递增栈,那么栈顶元素和栈中的第二个元素就是我们要的中心元素、左侧第一个比栈顶元素小的。而当前元素就是右侧第一个比栈顶元素小的。看图能更直观点(红框部分),这时候遍历的时候,栈中元素有0和2,当遇到1的时候,满足
while条件。
for (int right = 0; right < tmpHeight.length; right++) {// 一旦遇到某个节点比当前节点小了,就可以计算面积了。while (!stack.isEmpty() && tmpHeight[stack.peek()] > tmpHeight[right]) {// 栈顶元素(也就是我们说的中心柱子)int current = stack.pop();// left是左侧第一个比中心柱子矮的,right就是右侧第一个比中心柱子高的,// 因为在tmpHeight[stack.peek()] > tmpHeight[right]的前提约束下Integer left = stack.peek();// 计算面积res = Math.max(res, (right - left - 1) * tmpHeight[current]);}stack.push(right);
}
最终代码如下:
public int largestRectangleArea(int[] heights) {int res = 0;// 单调栈递增LinkedList<Integer> stack = new LinkedList<>();// 增加两个虚拟节点的临时数组int[] tmpHeight = new int[heights.length + 2];for (int i = 1; i <= heights.length; i++) {tmpHeight[i] = heights[i - 1];}for (int right = 0; right < tmpHeight.length; right++) {// 一旦遇到某个节点比当前节点小了,就可以计算面积了。while (!stack.isEmpty() && tmpHeight[stack.peek()] > tmpHeight[right]) {// 栈顶元素(也就是我们说的中心柱子)int current = stack.pop();// left是左侧第一个比中心柱子矮的,right就是右侧第一个比中心柱子高的,// 因为在tmpHeight[stack.peek()] > tmpHeight[right]的前提约束下Integer left = stack.peek();// 计算面积res = Math.max(res, (right - left - 1) * tmpHeight[current]);}stack.push(right);}return res;
}
