第五十七章 树状数组(二)
第五十七章 树状数组(二)
- 一、差分的缺陷
- 二、树状数组与差分
- 三、例题
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 样例 1 解释:
- 数据规模与约定
- 代码
一、差分的缺陷
差分的作用是能够在O(1)的时间内给一段区间加上相同的数字,最终查询的时候, 只需要对差分数组求前缀和即可。
但是,如果我们修改一次就想查询一次某个点的值的话。就说明我们需要不断地去求前缀和,即我们每次查询的时间复杂度都是O(n)O(n)O(n)的。这个是非常低效的。
因此,我们就可以利用树状数组来进行优化求解。
二、树状数组与差分
作者在之前的文章中介绍过树状数组与前缀和的关系,没有看过的话,作者建议先去看之前的文章:第五十六章 树状数组(一)
在前缀和+树状数组的题目中,我们是将原数组包装成了树状数组。
而在差分+树状数组的题目中,我们需要将原数组的差分数组写作树状数组的形式。
这样的话,如果给原数组[l,r]内的元素加上一个x的话,我们只需要操作差分数组中的两个点即可。这就又转化为我们在之前的文章中介绍的树状数组的三个函数。
三、例题
洛谷:P3368 【模板】树状数组 2
题目描述
如题,已知一个数列,你需要进行下面两种操作:
-
将某区间每一个数加上 xxx;
-
求出某一个数的值。
输入格式
第一行包含两个整数 NNN、MMM,分别表示该数列数字的个数和操作的总个数。
第二行包含 NNN 个用空格分隔的整数,其中第 iii 个数字表示数列第 $i $ 项的初始值。
接下来 MMM 行每行包含 222 或 444个整数,表示一个操作,具体如下:
操作 111: 格式:1 x y k 含义:将区间 [x,y][x,y][x,y] 内每个数加上 kkk;
操作 222: 格式:2 x 含义:输出第 xxx 个数的值。
输出格式
输出包含若干行整数,即为所有操作 222 的结果。
样例 #1
样例输入 #1
5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4
样例输出 #1
6
10
提示
样例 1 解释:
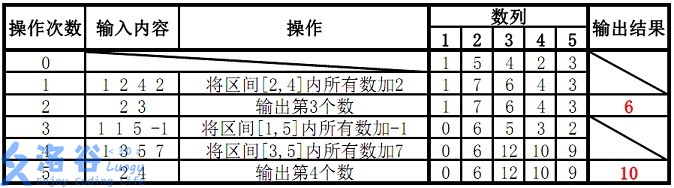
故输出结果为 6、10。
数据规模与约定
对于 30%30\%30% 的数据:N≤8N\le8N≤8,M≤10M\le10M≤10;
对于 70%70\%70% 的数据:N≤10000N\le 10000N≤10000,M≤10000M\le10000M≤10000;
对于 100%100\%100% 的数据:1≤N,M≤5000001 \leq N, M\le 5000001≤N,M≤500000,1≤x,y≤n1 \leq x, y \leq n1≤x,y≤n,保证任意时刻序列中任意元素的绝对值都不大于 2302^{30}230。
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 5e5 + 10;
int a[N], b[N], tree[N];
int n, m;int lowbits(int x)
{return x & -x;
}void add(int pos, int x)
{for(int i = pos; i <= n; i += lowbits(i))tree[i] += x;
}int quary(int pos)
{int res = 0;for(int i = pos; i; i -= lowbits(i))res += tree[i];return res;
}void solve()
{cin >> n >> m;for(int i = 1; i <= n; i ++ )cin >> a[i];for(int i = 1; i <= n; i ++ ){b[i] = a[i] - a[i - 1];add(i, b[i]);}while(m -- ){int op;cin >> op;if(op == 1){int l, r, d;cin >> l >> r >> d;add(l, d);add(r + 1, -d);}else{int pos;cin >> pos;cout << quary(pos) << endl;}}}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);solve();
}
