自抗扰控制ADRC之微分器TD
目录
前言
1 全程快速微分器
1.1仿真分析
1.2仿真模型
1.3仿真结果
1.4结论
2 Levant微分器
2.1仿真分析
2.2仿真模型
2.3仿真结果
3.总结
前言
工程上信号的微分是难以得到的,所以本文采用微分器实现带有噪声的信号及其微分信号提取,从而实现无需测量速度信号的控制。并且结合控制对象简单的用PID进行控制,即TD微分器+PID控制。
1 全程快速微分器
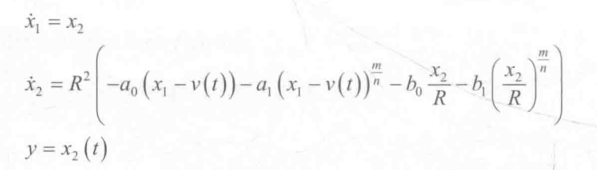
其中:
①x1为带有噪音的信号,也是TD的第一个状态变量,同理x2为信号的微分;
②R>0;a0、a1、b0、b1≥0;m和n为大于0的奇数,且m<n;
③当a1=b1=0时,上述微分器为线性微分器。
1.1仿真分析
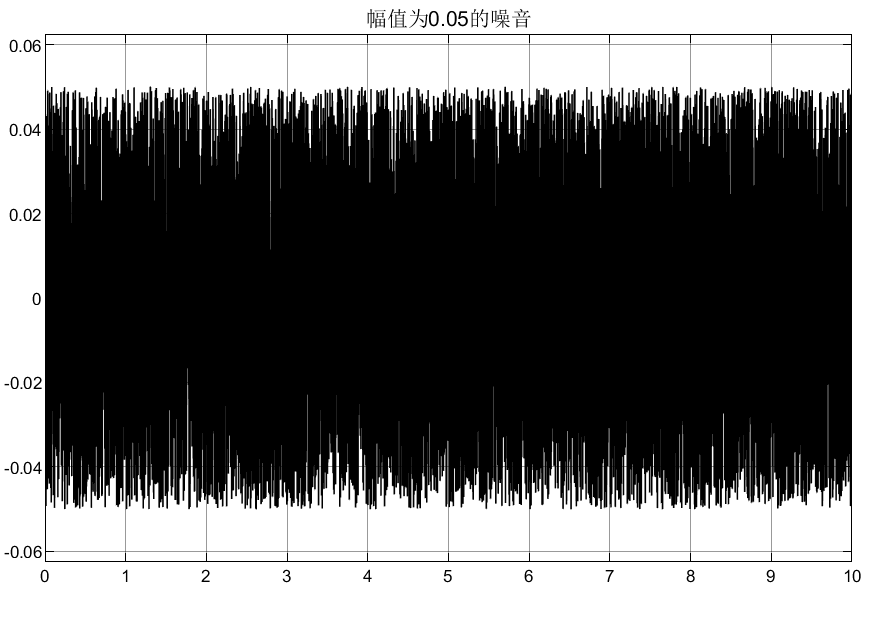
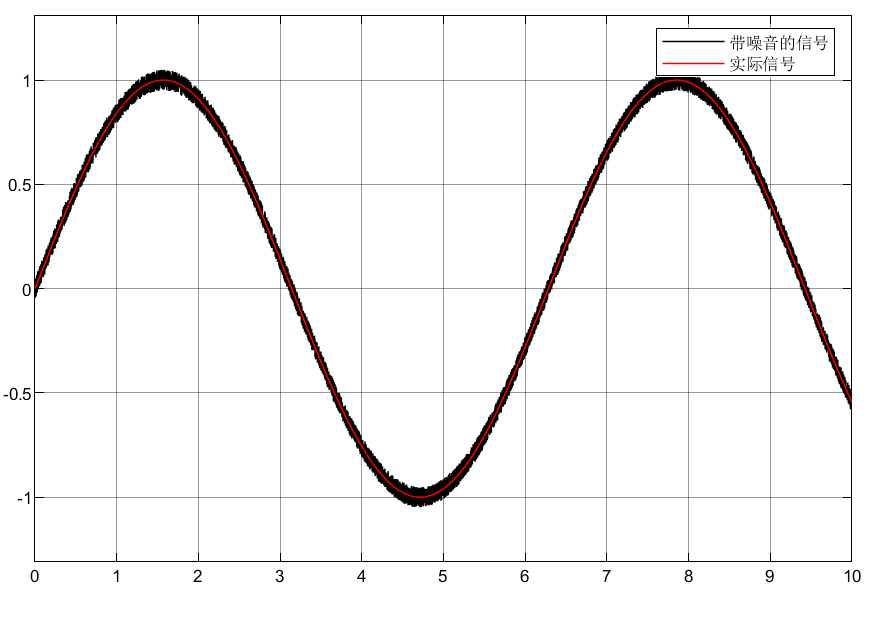
取R=1/0.05, a=0.1,b=0.1,已知输入信号为v(t)= sint,并且带有噪声信号,噪声的幅值为0.05,采用连续的全程快速微分器提取信号及信号的微分。
1.2仿真模型

1.3仿真结果
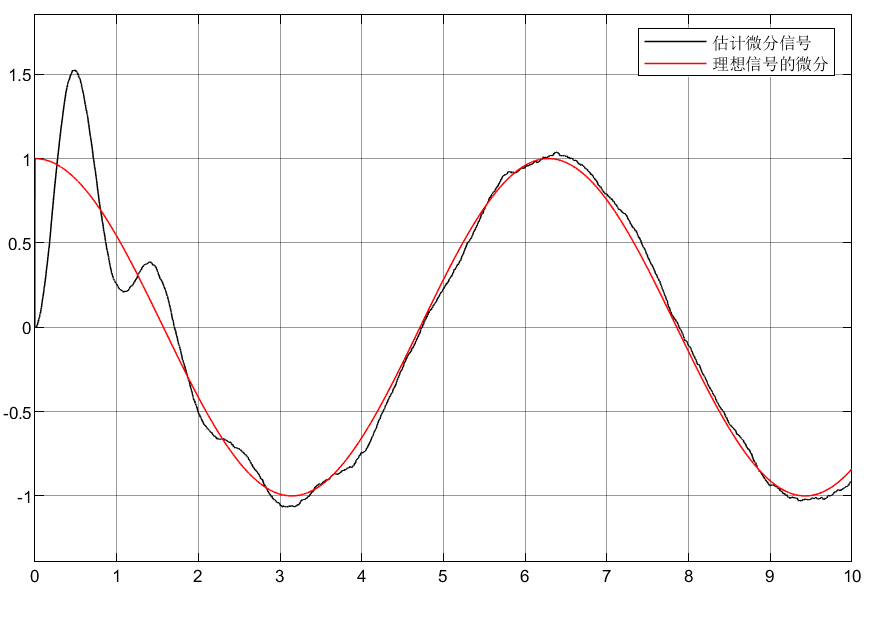
1.4结论
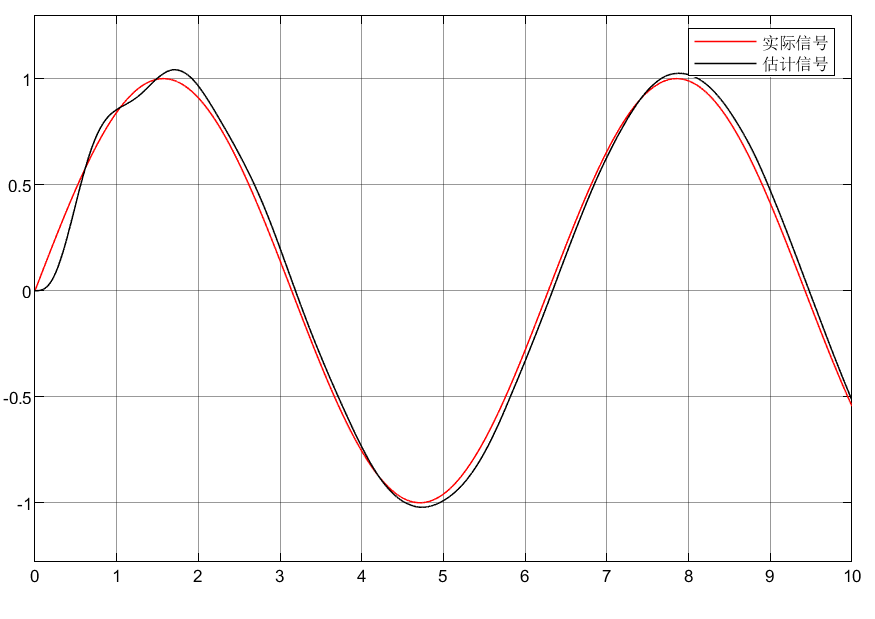
①可以看到虽然和实际信息有些偏差,但是估计的效果还算可以。
②对于a1、b1≠0的非线性微分器好像调节效果和线性差不多,即a1、b1、m、n调节没效果?
③位移信号可以调节的很好,但是会牺牲微分信号。
④仿真注意:(1)噪声模块的采样时间为继承采样时间;(2)simulink仿真求解步长为定步长0.001
2 Levant微分器
微分器需要对信号的测量误差和输入噪声具有鲁棒性,而Levant微分器是基于滑模奇数的非线性微分器,其二阶微分器表达形式为:
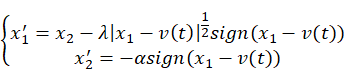

对于Lipschitz的定义部分可参考下面博客的3.1部分:
基于LMI的非线性混沌系统滑模控制_Mr. 邹的博客-CSDN博客
注:虽然这类微分器具有滑模控制的鲁棒性,但是对于Levant微分器,需要事先知道输入信号v(t)导数的Lipschitz常数上界,才能设计微分器参数,这就限制了输入信号的类型。而且,对于这种微分器,抖振现象不可避免。
2.1仿真分析
同样取上述的噪音信号及其微分进行估计,选取参数:
①Lipschitz的常数上界为1,即C = 1,所以α > 1,取α = 18;
②λ > 4*C*(α+C)/(α-C),得λ≥4.4706,所以取λ = 6。
2.2仿真模型
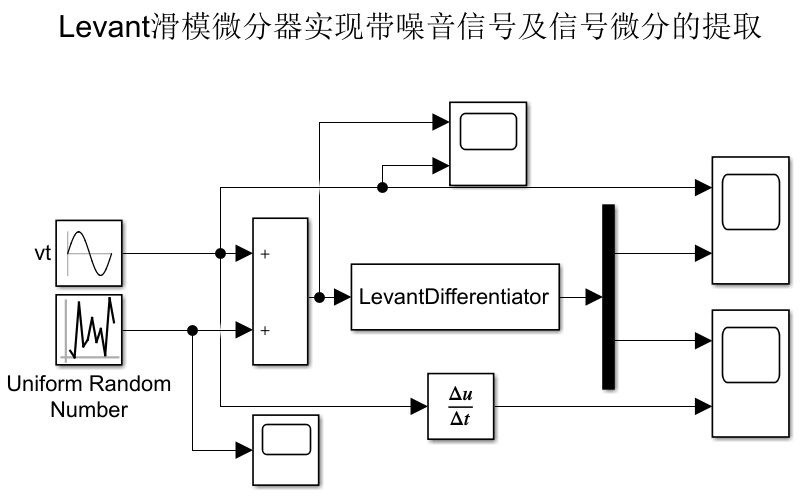
2.3仿真结果
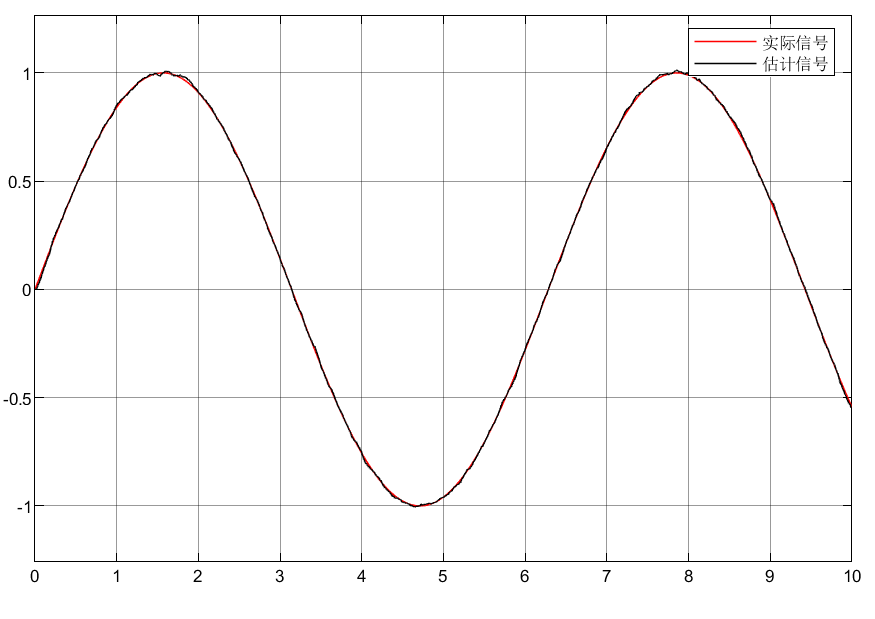
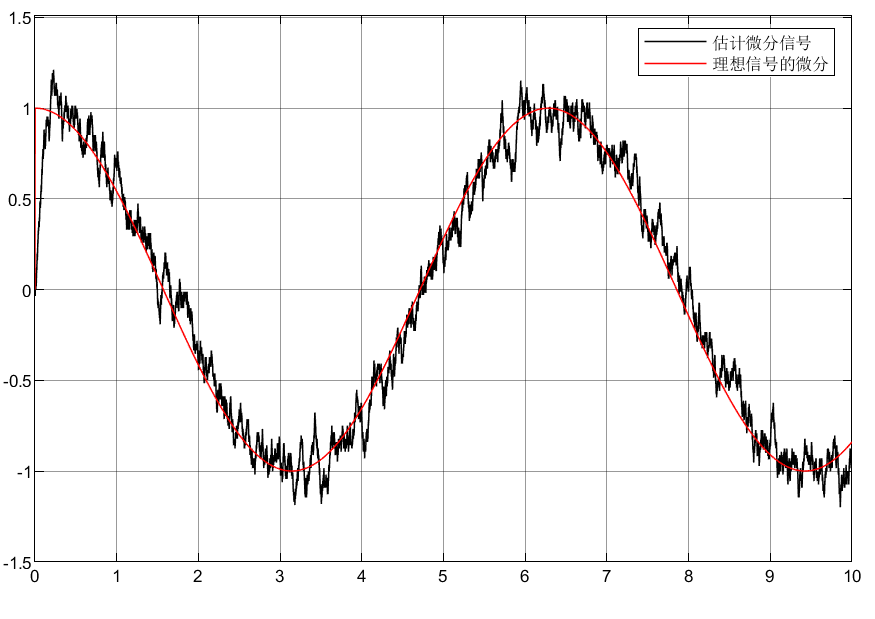
3.总结
①可以看到两种微分器都能将实现带噪声信号的估计,虽然有一定的误差
②信号的微分估计的稍差一些
③注意仿真时噪声模块的采样时间设定为继承采样时间:-1;且simulink设定为定步长0.001的求解器。
