24考研数据结构-图的存储结构邻接矩阵
目录
- 6.3 储存结构(邻接表表示法)
- 1. 储存方式
- 2. 结构
- 3. 图的邻接表存储表示(算法)
- 4. 结论
- 5. 邻接矩阵和邻接表的对比
- 邻接矩阵
- 优点:
- 缺点:
- 邻接表
- 优点:
- 缺点:
- 邻接矩阵与邻接表的关系
- 6.4.拓展存储结构(十字链表,邻接多重表)很绕多理解
- 1. 十字链表(存储有向图)
- 2. 邻接多重表(存储无向图)
- 6.5 四种存储结构的对比
6.3 储存结构(邻接表表示法)
1. 储存方式
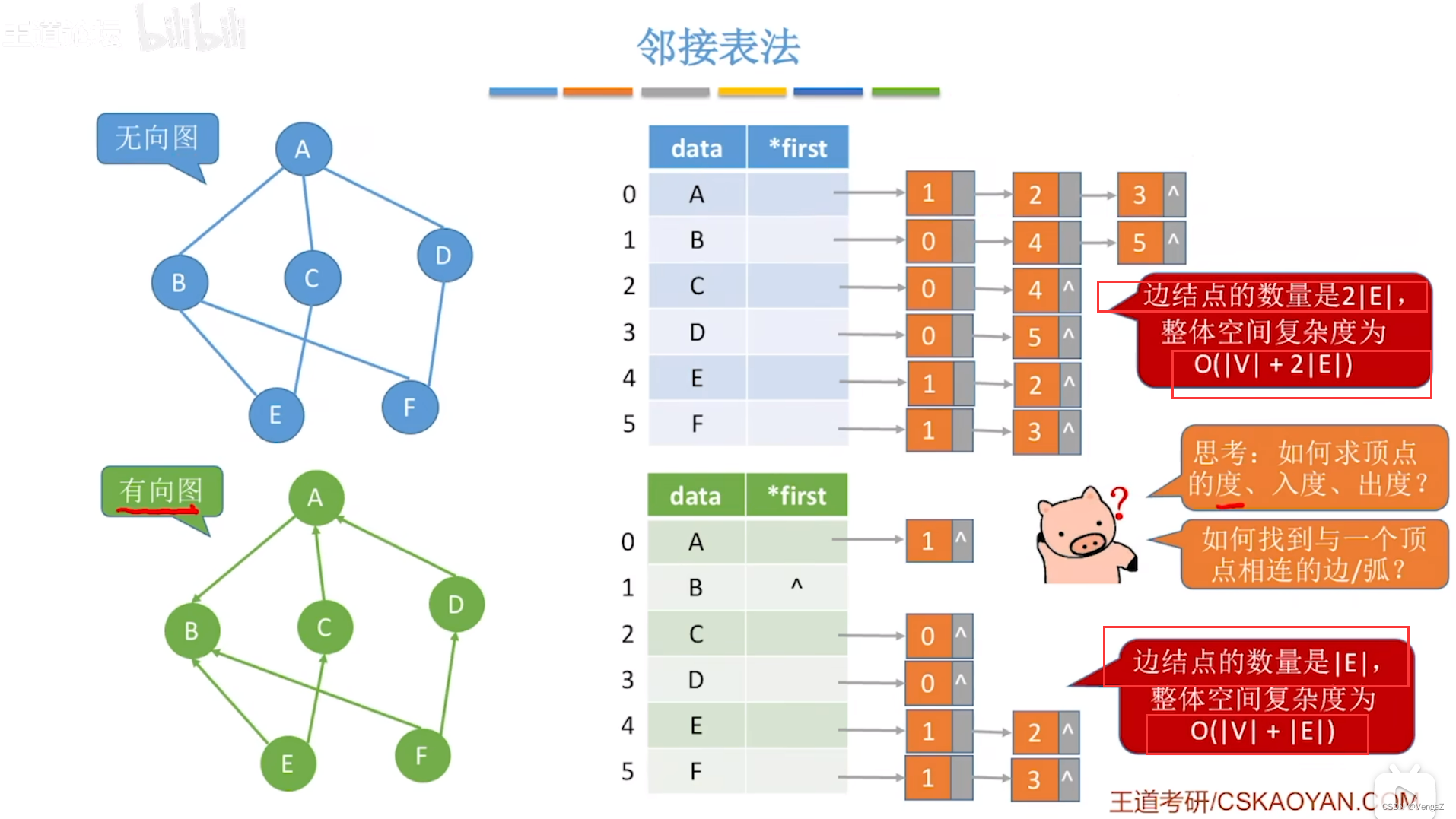
2. 结构
【1】顶点的结点结构
———————
| data | firstarc |
———————
data数据域:储存顶点vi
firstarc链域:指向链表中第一个结点
【2】弧的结点结构
——————————
| adjvex | info | nextarc |
——————————
adjvex邻接点域:与顶点vi邻接的点在图中的位置
info数据域:储存和边相关的信息,如权值
nextarc链域:与顶点vi的点在图中的位置
3. 图的邻接表存储表示(算法)
#define MAX_VERTEXT_NUM 20
//建立边结点
typedef struct ArcNode {int adjvex; // 该弧所指向的顶点的位置struct ArcNode *nextarc; // 指向下一条弧InfoType *info; // 该弧相关信息(可选)
}ArcNode;
// 顶点结点
typedef struct VNode{VertexType data; // 顶点信息ArcNode *firstarc; // 指向第一条依附该顶点的弧
}VNode,AdjList[MAX_VERTEXT_NUM];
//邻接表
typedef struct {Adjlist vertices;int vexnum,arcnum;int kind;
}ALGraph; //建立邻接表算法
//初始化一个结点总数为num的图,k为图的类型,num为结点总数
void InitG(ALGraph G,enum GraphKind k,int num)
{G.kind=k;G.vexnum=num;G.vertices=new VNode[vexnum];for(int i=0;i<G.vexnum;i++){G.vertices[i].Firstarc=NULL;cin>>G.vertics[i].data;}
}//有向图(网)增加弧的算法,将弧(from,to,weight)加入图
void InsertArc(ALGragh G,int from,int to,int weight)
{ArcNode *s=new ArcNode;s->weight=weight;s->adjvex=to;s->nextarc=G.vertices[from].firstarc;//插到链表vertices[from]的头G.vertices[from].firstarc=s;
}4. 结论
(1)在邻接表中,同一条边对应两个结点。
(2)无向图中顶点v的度:等于v 对应的链表的长度;但是,在有向图中,要求顶点A的的入度,则需要遍历所有的顶点连接的链表,判断有几个存在顶点A;求出度,则是A顶点链表有几个点。
(3)判定两顶点v,w是否邻接:要看v对应的链表中有无对应的结点w(相反判断也行);
(4)对于一个图,给定的邻接表是并不唯一的(区分与邻接矩阵)
(5)增减边:要在两个单链表插入、删除结点;
(6)占用存储空间与顶点数、边数均有关;适用于边稀疏的图
注意,在有向图的邻接表中不易找到指向该顶点的弧。
邻接矩阵表示唯一,邻接表表示不唯一
5. 邻接矩阵和邻接表的对比
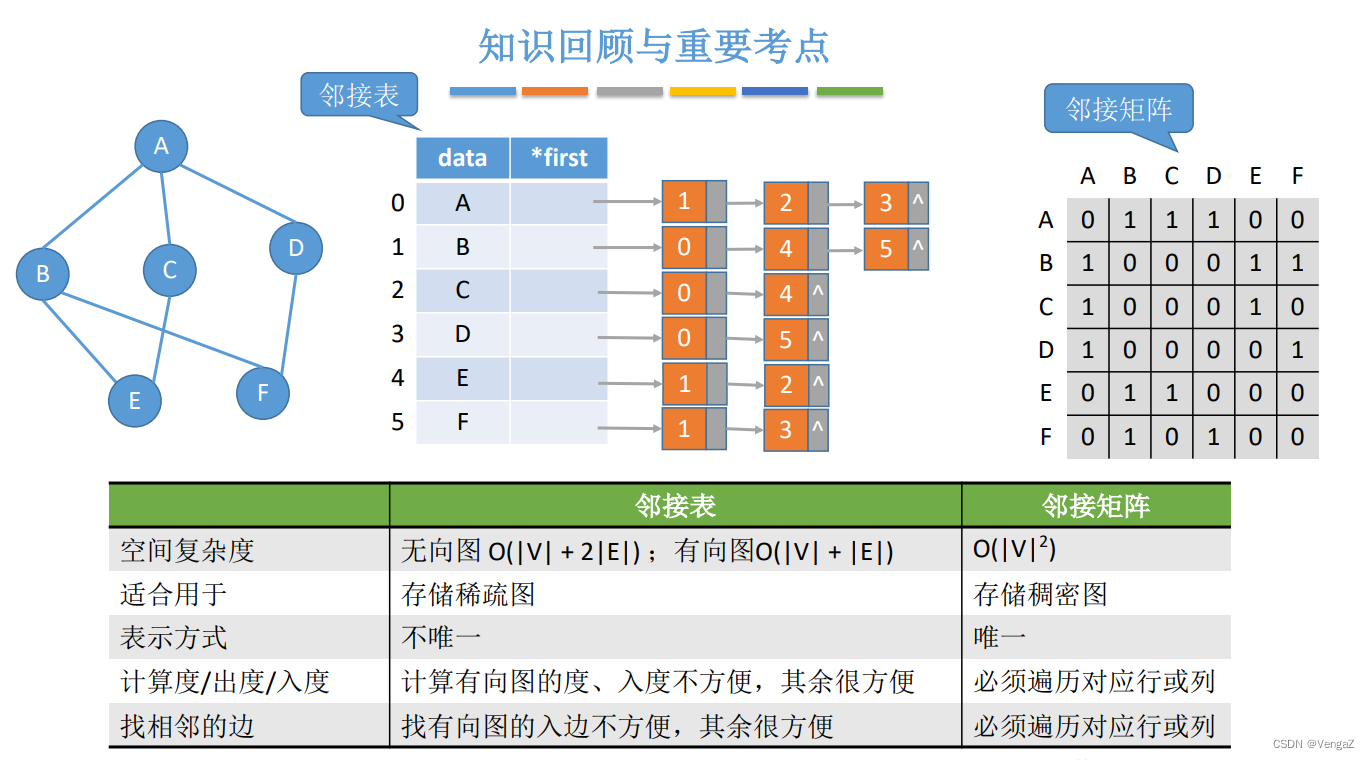
图是计算机科学中重要的数据结构之一,用于表示多对多的关系。在实际应用中,图可以用于表示网络拓扑、社交关系、路由算法等。对于图的存储结构,有两种常见的方式:邻接矩阵和邻接表。本文将介绍这两种存储结构的原理和特点,并对比它们之间的关系。
邻接矩阵
邻接矩阵是一种使用二维数组来表示图的存储结构。对于有n个节点的图,邻接矩阵是一个n*n的矩阵,其中的元素表示节点之间的关系。如果图中的节点i和节点j之间有边相连,则邻接矩阵中的第i行第j列的元素为1;否则,为0。
优点:
- 查询快速:由于邻接矩阵是一个二维数组,可以通过下标直接访问节点之间的关系,查询操作的时间复杂度为O(1)。
- 空间效率:在稠密图(边数接近节点数平方)中,邻接矩阵的存储效率较高。
缺点:
- 空间复杂度高:对于稀疏图(边数远小于节点数平方),邻接矩阵会浪费大量空间来表示不存在的边。
class Graph {
private:int V; // 节点数int** adjMatrix; // 邻接矩阵public:Graph(int vertices) {V = vertices;adjMatrix = new int*[V];for (int i = 0; i < V; i++) {adjMatrix[i] = new int[V];for (int j = 0; j < V; j++) {adjMatrix[i][j] = 0;}}}void addEdge(int src, int dest) {adjMatrix[src][dest] = 1;adjMatrix[dest][src] = 1;}// 其他操作...
};
邻接表
邻接表是一种使用链表来表示图的存储结构。对于有n个节点的图,邻接表是一个包含n个链表的数组,每个链表存储与节点i相邻的节点。
优点:
- 空间效率高:在稀疏图中,邻接表可以节省大量空间,只存储存在的边。
- 插入和删除快速:在邻接表中插入或删除边相对较快。
缺点:
- 查询效率低:在邻接表中查询节点i和节点j之间是否有边,需要遍历链表,平均时间复杂度为O(V)。
class Graph {
private:int V; // 节点数vector<list<int>> adjList; // 邻接表public:Graph(int vertices) {V = vertices;adjList.resize(V);}void addEdge(int src, int dest) {adjList[src].push_back(dest);adjList[dest].push_back(src);}// 其他操作...
};
邻接矩阵与邻接表的关系
邻接矩阵和邻接表是两种不同的图的存储结构,各自有着优缺点。对于边稠密的图,邻接矩阵可以提供较好的查询效率和空间效率;而对于边稀疏的图,邻接表则更加节省空间。
在实际应用中,我们需要根据具体的图的特点和操作需求来选择合适的存储结构。如果图是边稠密的,且需要频繁进行查询操作,邻接矩阵可能是一个不错的选择;如果图是边稀疏的,邻接表可以更好地节省空间。在有些情况下,我们也可以结合使用邻接矩阵和邻接表,充分发挥它们各自的优势,以满足实际需求。
综上所述,邻接矩阵和邻接表是图的两种常见存储结构,它们各自有着优缺点。在实际应用中,需要根据图的特点和操作需求进行选择,以达到最优的性能和空间效率。
6.4.拓展存储结构(十字链表,邻接多重表)很绕多理解
1. 十字链表(存储有向图)
- 空间复杂度:O(|V|+|E|)
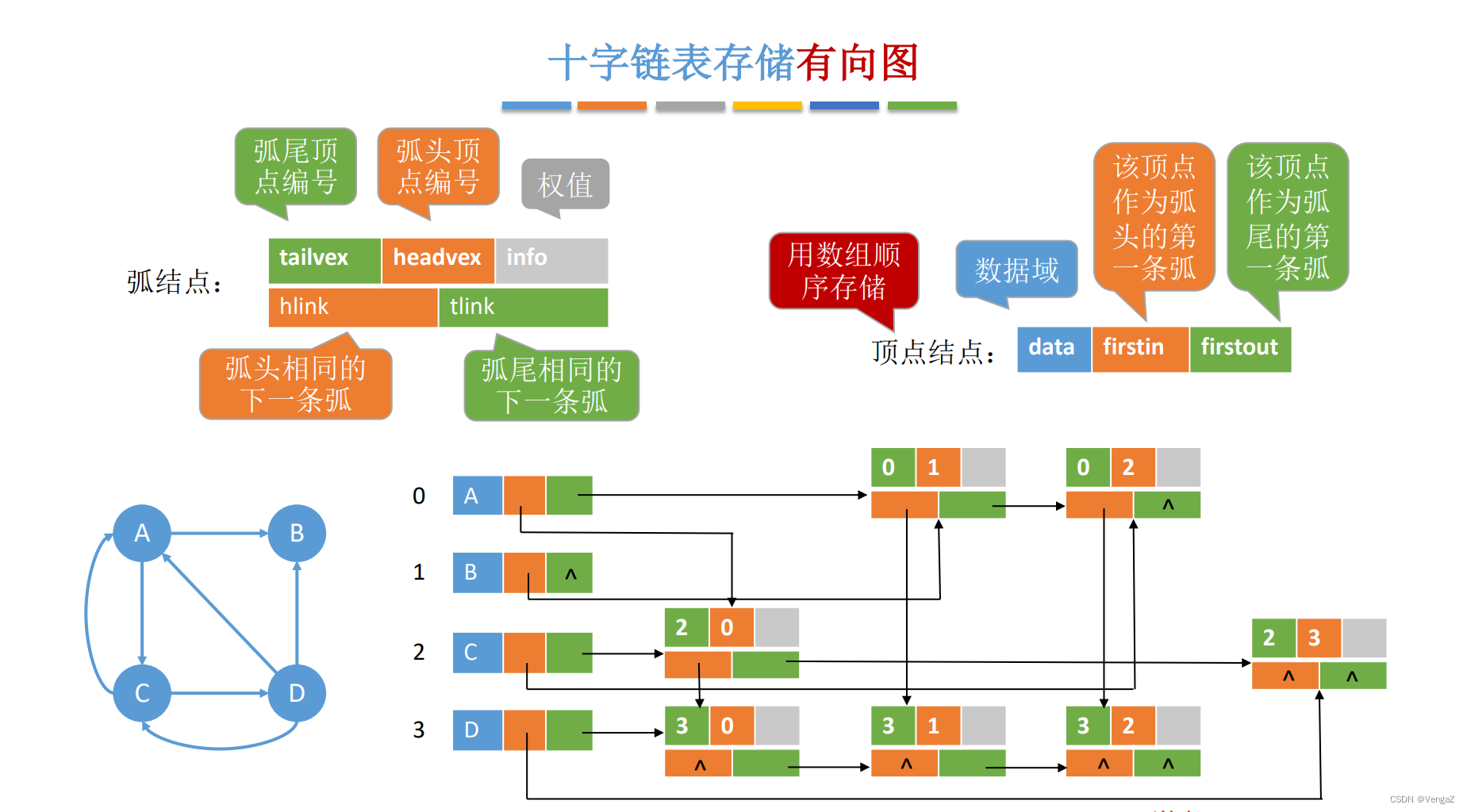
- 同层可找所有出边即出度(绿色)
- 不同层相连的即所有入边(橙色)
- 比邻接表空间复杂度的 v 2 v^2 v2更小

2. 邻接多重表(存储无向图)
- 解决无向图冗余信息的问题,空间大
- 删除边,删除结点操作更简单(只要顺着指针找,就跟删除链表结点一样)
- 空间复杂度:O(|V|+|E|),比邻接表的v+2e,因为不存储无关的结点
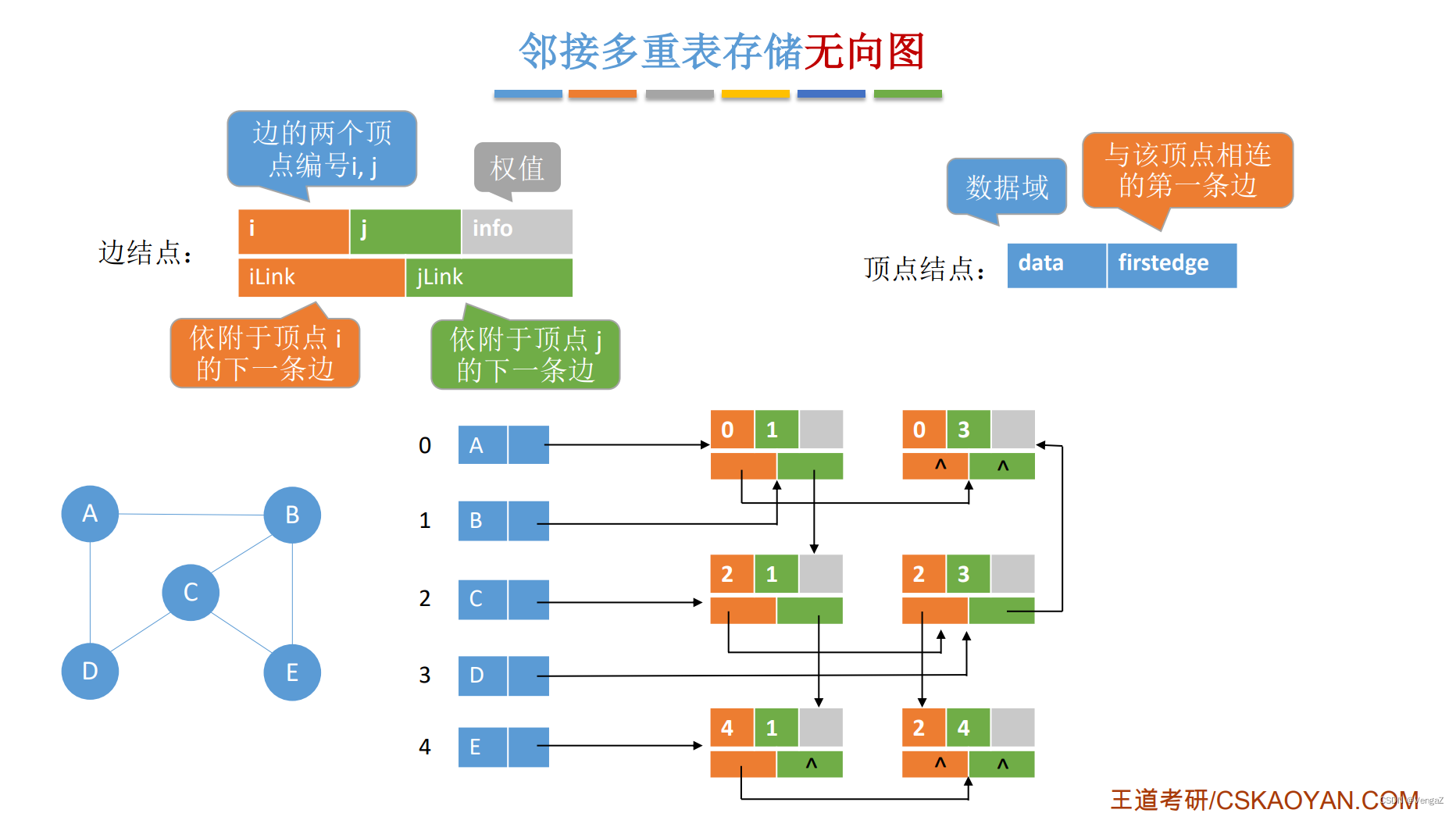
6.5 四种存储结构的对比

