LeetCode 42. 接雨水(动态规划 / 单调栈)
题目:
链接:LeetCode 42. 接雨水
难度:困难
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:
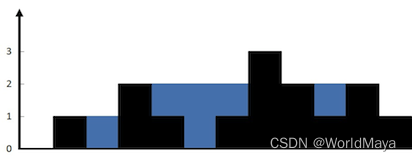
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
提示:
- n == height.length
- 1 <= n <= 2 * 104
- 0 <= height[i] <= 105
方法一:
动态规划:
按列求每一列能存的雨水时,应该求这一列左右最高的墙,其中较矮的墙与这一列高度的差值(>0)为当前列能存的雨水量。对于求左右最高的墙,我们可以用动态规划的方法做:
首先用两个数组,max_left [i] 代表第 i 列左边最高的墙的高度,max_right[i] 代表第 i 列右边最高的墙的高度。(一定要注意下,第 i 列左(右)边最高的墙,是不包括自身的)
对于 max_left我们其实可以这样求。
max_left [i] = Max(max_left [i-1],height[i-1])。它前边的墙的左边的最高高度和它前边的墙的高度选一个较大的,就是当前列左边最高的墙了。
对于 max_right我们可以这样求。
max_right[i] = Max(max_right[i+1],height[i+1]) 。它后边的墙的右边的最高高度和它后边的墙的高度选一个较大的,就是当前列右边最高的墙了。
得到了左右最高墙的结果,我们再用前面提到的方法按列求雨水量即可。
代码一:
class Solution {
public:int trap(vector<int>& height) {int n = height.size();int maxleft[n], maxright[n];maxleft[0] = 0, maxright[n - 1] = 0;for(int i = 1; i < n; i++){maxleft[i] = max(maxleft[i - 1], height[i - 1]);}for(int i = n - 2; i >= 0; i--){maxright[i] = max(maxright[i + 1], height[i + 1]);}int sum = 0;for(int i = 1; i < n - 1; i++){int num = min(maxleft[i], maxright[i]) - height[i];if(num > 0) sum += num;}return sum;}
};
时间复杂度O(N)。
空间复杂度O(N)。
方法二:
单调栈:
除了计算并存储每个位置两边的最大高度以外,也可以用单调栈计算能接的雨水总量。
维护一个单调栈,单调栈存储的是下标,满足从栈底到栈顶的下标对应的数组 height 中的元素递减。
从左到右遍历数组,遍历到下标 iii 时,如果栈内至少有两个元素,记栈顶元素为 top,top 的下面一个元素是 left,则一定有 height[left] ≥ height[top]。如果 height[i] > height[top],则得到一个可以接雨水的区域,该区域的宽度是 i−left−1,高度是 min(height[left], height[i]) − height[top],根据宽度和高度即可计算得到该区域能接的雨水量。
为了得到 left,需要将 top 出栈。在对 top 计算能接的雨水量之后,left 变成新的 top,重复上述操作,直到栈变为空,或者栈顶下标对应的 height 中的元素大于或等于 height[i]。
在对下标 i 处计算能接的雨水量之后,将 i 入栈,继续遍历后面的下标,计算能接的雨水量。遍历结束之后即可得到能接的雨水总量。
代码二:
class Solution {
public:int trap(vector<int>& height) {int n = height.size();stack<int> s; // 单调栈int sum = 0;for(int i = 0; i < n; i++){while(!s.empty() && height[i] > height[s.top()]) {int bottom = height[s.top()];s.pop();int left, left_i;if(s.empty()) {left = 0;left_i = 0;}else {left = height[s.top()];left_i = s.top();}int wallHeight = min(left, height[i]);int num = (wallHeight - bottom) * (i - left_i - 1);if(num > 0) sum += num;}s.emplace(i);}return sum;}
};
时间复杂度O(N),N是数组 height 长度,每个元素只会入栈和出栈一次。
空间复杂度O(N),栈空间最多为N。
