使用梯度下降的线性回归(Matlab代码实现)
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
👨💻4 Matlab代码
💥1 概述
梯度下降法,是一种基于搜索的最优化方法,最用是最小化一个损失函数。梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数,即无约束优化问题时,梯度下降(Gradient Descent)是最常采用的方法之一,另一种常用的方法是最小二乘法。在求解损失函数的最小值时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数和模型参数值。
📚2 运行结果


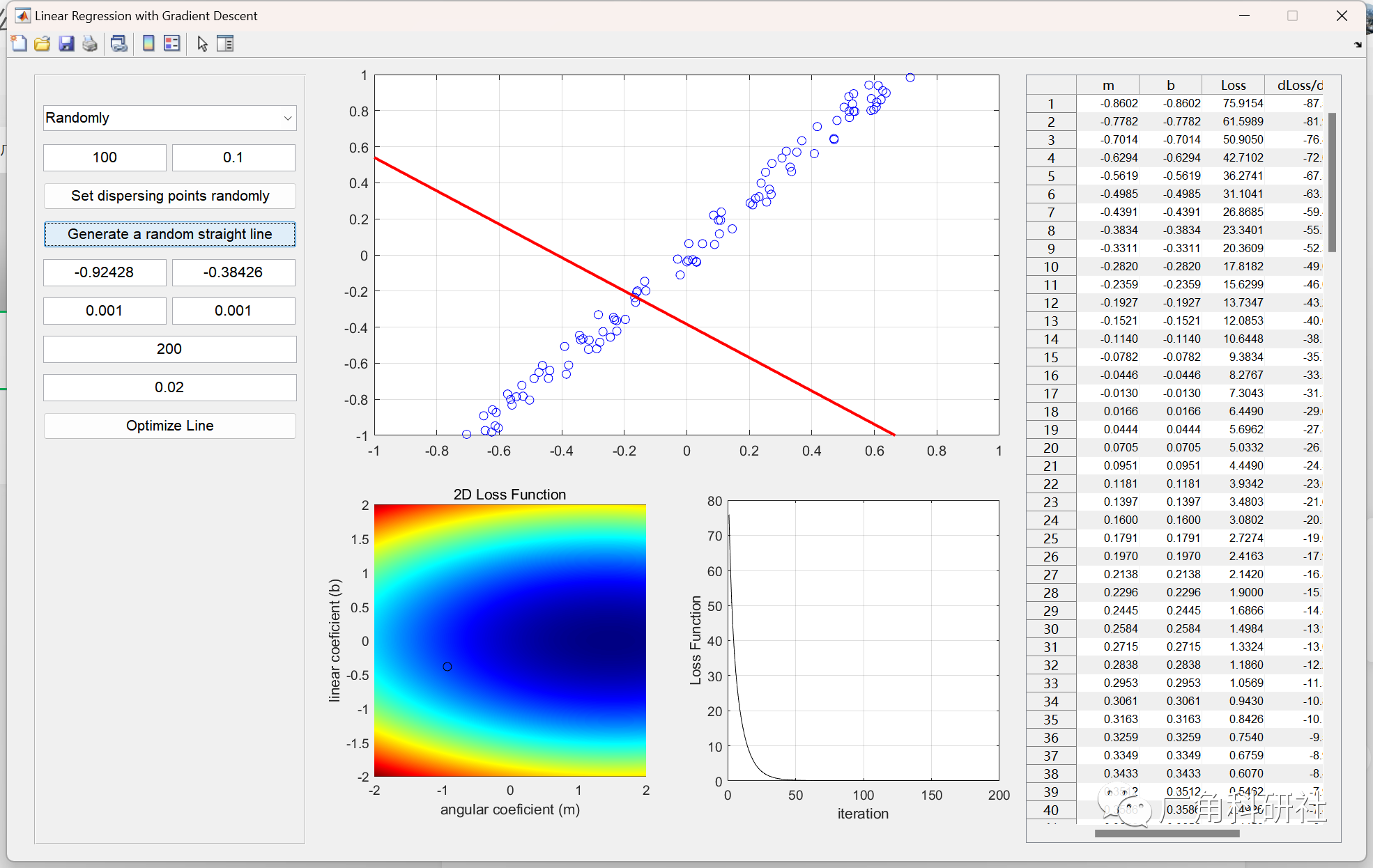
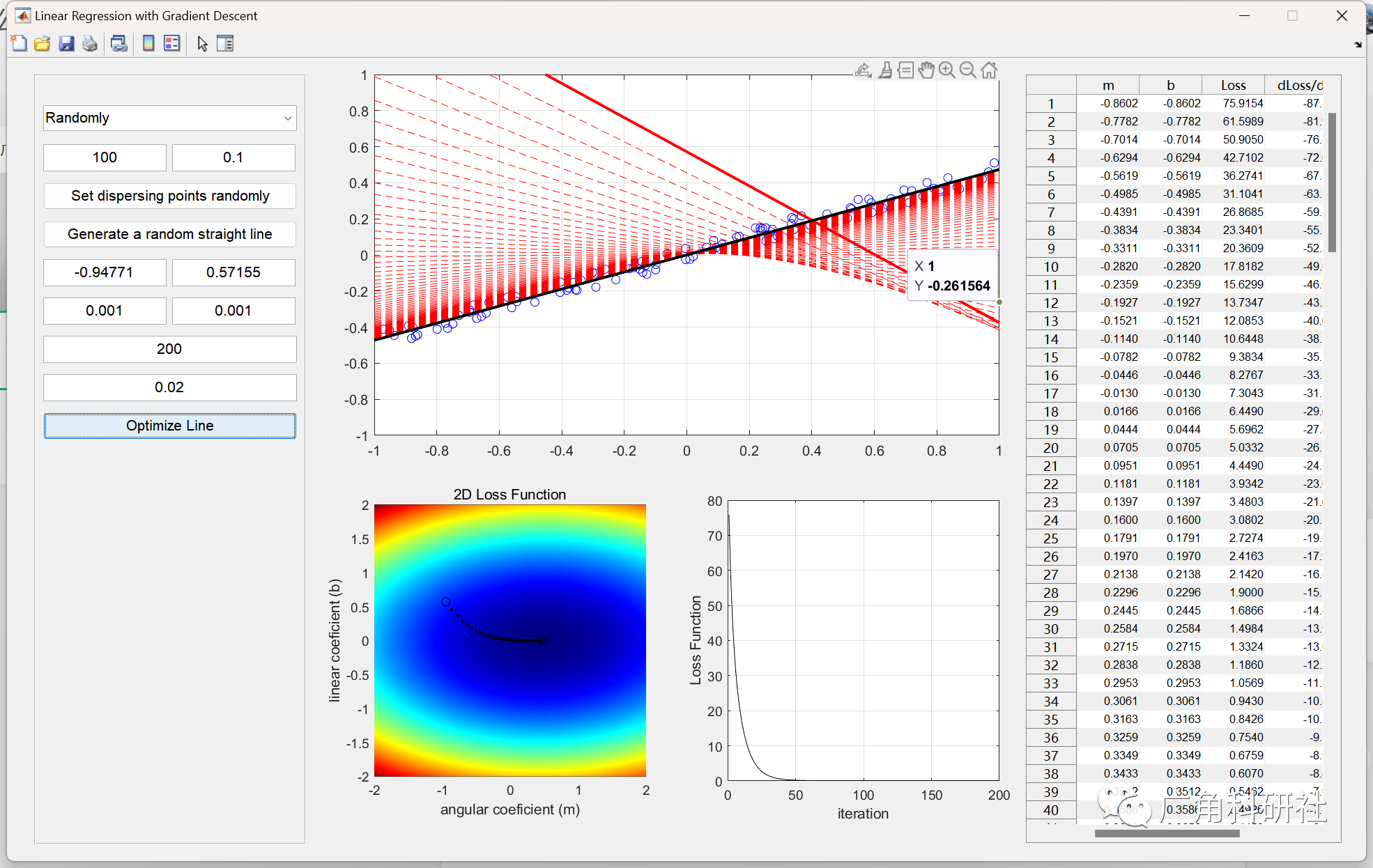
主函数部分代码:
%--------------------------------------------------------------------------
%LOCAL FUNCTIONS
%--------------------------------------------------------------------------
function generateLossGraph(N,x_d,y_d)
range = 2;
M_ = 500;
b_ = linspace(-range,range,M_);
m_ = linspace(-range,range,M_);
[B,M] = meshgrid(b_,m_);
reg = zeros([1,N]);
loss_function = zeros(M_);
for j=1:M_
for i=1:M_
for k=1:N
reg(1,k) = m_(j)*x_d(k) + b_(i);
end
loss_function(i,j) = sum((reg-y_d).^2);
end
end
axes(loss_function_graph)
pcolor(B,M,loss_function)
xlabel('angular coeficient (m)')
ylabel('linear coeficient (b)')
title('2D Loss Function')
shading interp
axis image
colormap jet
end
function delete_a_graph_component_from_its_tag(obj_handle,tag_name)
obj = findobj(obj_handle,'Tag',tag_name);
if(~isempty(obj))
delete(obj)
end
end
function [posX,posY,Width,Height]=centralizeWindow(Width_,Height_)
%Size of the screen
screensize = get(0,'Screensize');
Width = screensize(3);
Height = screensize(4);
posX = (Width/2)-(Width_/2);
posY = (Height/2)-(Height_/2);
Width=Width_;
Height=Height_;
end
end
🎉3 参考文献
[1]李兴怡,岳洋.梯度下降算法研究综述[J].软件工程,2020,23(02):1-4.DOI:10.19644/j.cnki.issn2096-1472.2020.02.001.
