数学知识(二)
一、裴蜀定理
对于任意整数a,b,一定存在非零整数x,y,使得 ax + by = gcd(a,b)
#include<iostream>
#include<algorithm>using namespace std;int exgcd(int a,int b,int &x,int &y)
{if(!b){x = 1,y = 0;return a;}int d = exgcd(b,a % b,y,x);y -= a / b * x;return d;
}int main()
{int n;scanf("%d",&n);while(n --){int a,b,x,y;scanf("%d%d",&a,&b);exgcd (a,b,x,y);printf("%d%d\n",x,y);}return 0;
}二、高斯消元
步骤:枚举每一列,取列c
- 1、找到绝对值最大的一行
- 2、将该行换到最上面
- 3、将该行第一个数变为1(与该行其它数的比值不改变)
- 4、将下面所有行的第c列消为零
#include<iostream>
#include<cmath>
#include<algorithm>using namespace std;const int N = 110;
const double eps = 1e-6;int n;
double a[N][N];int gauss()
{int c,r;for(c = 0,r = 0; c < n;c ++){//找到绝对值最大的一行int t = r;for(int i = r; i < n; i ++)if(fabs(a[i][c]) > fabs(a[t][c])) t = i;if(fabs(a[t][c]) < eps) continue;//将该行换到最上方for(int i = c;i <= n;i ++) swap(a[t][i],a[r][i]);//将该行第一个数变为1for(int i = n;i >= c; i --) a[r][i] /= a[r][c];//将下面所有行消为0for(int i = r + 1;i < n;i ++)if(fabs(a[i][c]) > eps)for(int j = n;j >= c;j --)a[i][j] -= a[r][j] * a[i][c];r ++;}if(r < n){for(int i = r;i < n;i ++)if(fabs(a[i][n]) > eps)return 2; //无解return 1; //有无穷多组解}for(int i = n - 1;i >= 0;i --)for(int j = i + 1;j < n;j ++)a[i][n] -= a[i][j] * a[j][n];return 0; //存在唯一的解
}三、求组合数
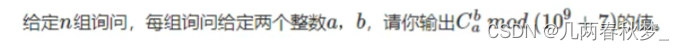
#include<iostream>
#include<cmath>
#include<algorithm>using namespace std;const int N = 2010,mod = 1e9 + 7;
int c[N][N];//初始化
void init()
{for(int i = 0;i < N;i ++)for(int j = 0;j <= i;j ++){if(!j) c[i][j] = 1;else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;}}
int main()
{init();int n;scanf("%d",&n);while(n --){int a,b;scanf("%d%d",&a,&b);printf("%d\n",c[a][b]);}return 0;
}
第二种方法:
#include<iostream>
#include<algorithm>
#include<cmath>using namespace std;typedef long long LL;
const int N = 100010,mod = 1e9 + 7;int fact[N],infact[N];int qmi(int a,int k,int p)
{int res = 1;while(k){if(k & 1) res = (LL) res *a % p;a = (LL)a * a % p;k >>= 1;}return res;
}int main()
{fact[0] = infact[0] = 1;for(int i = 1;i < N;i ++){fact[i] = (LL)fact[i - 1] * i % mod;infact[i] = (LL)infact[i - 1] * qmi(i,mod - 2,mod) % mod;}int n;scanf("%d",&n);while(n --){int a,b;scanf("%d%d",&a,&b);printf("%d\n",(LL)fact[a] * infact[b] % mod * infact[a - b] % mod);}return 0;
}
