排序进行曲-v3.0
小程一言
这篇文章是在排序进行曲2.0之后的续讲,
这篇文章主要是对归并排序进行细致分析,以及操作。
希望大家多多支持
图片: 
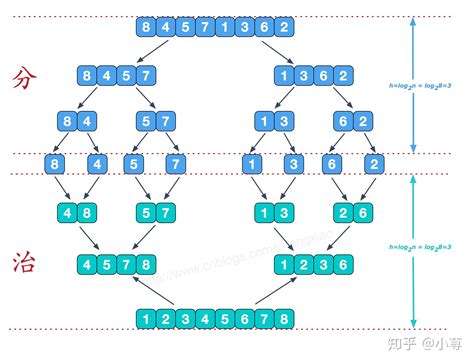
归并排序
归并排序是一种分治算法,它将一个待排序的数组分成两个子数组,分别对这两个子数组进行排序,然后再将
两个有序的子数组合并为一个有序的数组。这个过程不断地递归进行,直到最后将整个数组排序完成。
步骤
分割(Divide):将待排序的数组不断地二分,直到分成单个元素的子数组。这个过程可以通过递归实现。递归的终止条件是数组的长度为1。合并(Merge):将相邻的两个有序子数组合并为一个有序的子数组。合并的方法是比较两个子数组的第一个元素,将较小的元素放在新的子数组中,并将该元素从原子数组中移除。然后继续比较两个子数组的新的第一个元素,重复这个过程,直到其中一个子数组为空。将剩余的另一个子数组直接拼接到新的子数组的末尾。递归合并(Recursive Merge):对每个单个元素的子数组进行排序和合并。当子数组长度为1时,它已经是有序的,直接返回该子数组即可。对于长度大于1的子数组,先将其分割成两个子数组,然后分别对这两个子数组进行递归合并,得到两个有序的子数组。最后将这两个有序的子数组进行合并,得到一个更大的有序子数组。
举例
假设我们要对数组 [5, 3, 8, 2, 9, 1] 进行排序。分割(Divide):首先将数组分成两个子数组,即 [5, 3, 8] 和 [2, 9, 1]。递归合并(Recursive Merge):对两个子数组分别进行递归合并排序。首先对 [5, 3, 8] 进行递归合并排序,得到有序子数组 [3, 5, 8]。然后对 [2, 9, 1] 进行递归合并排序,得到有序子数组 [1, 2, 9]。合并(Merge):将两个有序子数组 [3, 5, 8] 和 [1, 2, 9] 进行合并。比较两个子数组的第一个元素,将较小的元素放入新的子数组中,并将该元素从原子数组中移除。依次比较,得到新的子数组[1, 2, 3, 5, 8, 9]。最终,整个数组 [5, 3, 8, 2, 9, 1] 经过归并排序后,得到有序数组 [1, 2, 3, 5, 8, 9]。
总结
这个例子展示了归并排序的过程,通过不断地分割和合并子数组,最终将整个数组排序。在每一次合并过程中,我们都是将两个有序的子数组合并为一个有序的子数组,这保证了最终得到的整个数组是有序的。

)### 复杂度分析
归并排序的时间复杂度为 O(nlogn),空间复杂度为 O(n)。
时间复杂度分析:
分割(Divide):每次将数组分割成两个子数组,分割的时间复杂度为 O(logn)。因为每次分割都将数组的大小减半,所以需要进行 logn 次分割。
合并(Merge):对于每一次合并操作,需要比较两个子数组的元素并将较小的元素放入新的子数组中,合并的时间复杂度为 O(n)。因为每次合并都是将两个子数组的元素全部比较一遍,所以需要进行 n 次合并。
递归合并(Recursive Merge):对于长度为 n 的数组,需要进行 logn 次递归合并,每次递归合并的时间复杂度为 O(n)。所以总的时间复杂度为 O(nlogn)。
空间复杂度分析:
在每次递归合并的过程中,需要创建临时数组来存储合并后的子数组,临时数组的空间复杂度为 O(n)。
在每次递归合并完成后,临时数组会被销毁,所以整个归并排序的空间复杂度为 O(n)。
注意
归并排序是一种稳定的排序算法,因为在合并的过程中,如果两个元素相等,我们会先将左边的元素放入新的子数组中,这样可以保持原始数组中相等元素的相对顺序不变。
应用场景
排序问题:归并排序可以用于对数组、链表等数据结构进行排序。它的时间复杂度为O(nlogn),在处理大规模数据集时表现较好。大规模数据的排序:归并排序适用于需要对大规模数据进行排序的场景。由于归并排序是一种分治算法,可以将大规模数据分割成较小的子问题进行排序,然后再将排序好的子问题合并起来。外部排序:归并排序是一种适用于外部排序的算法。外部排序是指需要处理的数据量大于计算机内存容量,需要将数据存储在外部存储介质(如硬盘)中进行排序。归并排序的特点是每次只需要读取一部分数据到内存中进行排序,然后将排序好的数据写回外部存储介质。并行计算:归并排序可以通过并行计算的方式提高排序的效率。由于归并排序的分治特性,可以将大规模数据分割成多个子问题进行排序,然后再将排序好的子问题合并起来。这种并行计算的方式可以利用多核处理器或分布式计算环境来加速排序过程。
总结
归并排序适用于排序问题,特别是大规模数据的排序和外部排序场景。它具有稳定的时间复杂度和较好的并行性能,因此在实际应用中被广泛使用。
实际举例
数组排序:归并排序可以用于对数组进行排序。例如,给定一个整数数组,可以使用归并排序将数组中的元素按照升序进行排序。链表排序:归并排序也可以用于对链表进行排序。例如,给定一个链表,可以使用归并排序将链表中的节点按照升序进行排序。文件排序:归并排序可以用于对大规模文件进行排序。例如,当需要对一个非常大的文件进行排序时,可以使用归并排序算法将文件分割成多个较小的部分,分别对这些部分进行排序,然后再将排序好的部分合并起来。数据库排序:归并排序可以用于对数据库中的数据进行排序。例如,在某个数据库表中有大量的数据需要按照某个字段进行排序,可以使用归并排序算法将数据分割成多个较小的部分,分别对这些部分进行排序,然后再将排序好的部分合并起来。外部排序:归并排序是一种适用于外部排序的算法。外部排序是指需要处理的数据量大于计算机内存容量,需要将数据存储在外部存储介质(如硬盘)中进行排序。归并排序的特点是每次只需要读取一部分数据到内存中进行排序,然后将排序好的数据写回外部存储介质。
Other
这些例子只是归并排序在实际中的一些应用,实际上归并排序的思想和方法也可以应用于其他问题,只需要将问题分割成更小的子问题,并将子问题的结果合并起来。
代码实现
public class MergeSort {public static void mergeSort(int[] arr) {if (arr == null || arr.length <= 1) {return;}int[] temp = new int[arr.length];mergeSort(arr, 0, arr.length - 1, temp);}private static void mergeSort(int[] arr, int start, int end, int[] temp) {if (start >= end) {return;}int mid = start + (end - start) / 2;mergeSort(arr, start, mid, temp);mergeSort(arr, mid + 1, end, temp);merge(arr, start, mid, end, temp);}private static void merge(int[] arr, int start, int mid, int end, int[] temp) {int left = start;int right = mid + 1;int index = start;while (left <= mid && right <= end) {if (arr[left] <= arr[right]) {temp[index++] = arr[left++];} else {temp[index++] = arr[right++];}}while (left <= mid) {temp[index++] = arr[left++];}while (right <= end) {temp[index++] = arr[right++];}for (int i = start; i <= end; i++) {arr[i] = temp[i];}}public static void main(String[] args) {int[] arr = {5, 2, 8, 4, 9, 1, 3, 7, 6};mergeSort(arr);System.out.println("Sorted array: " + Arrays.toString(arr));}
}

结果
运行以上代码,输出结果为:Sorted array: [1, 2, 3, 4, 5, 6, 7, 8, 9],表示归并排序对给定的数组进行了升序排序。
解释
在mergeSort方法中,首先判断数组的长度是否小于等于1,如果是,则直接返回。然后创建一个临时数组temp,并调用mergeSort方法对数组进行递归排序。在mergeSort方法中,首先计算出数组的中间位置mid,然后分别对左半部分和右半部分进行递归排序,最后调用merge方法将排序好的左右两部分合并起来。在merge方法中,使用双指针分别指向左半部分和右半部分的起始位置,比较两个指针所指的元素大小,将较小的元素放入临时数组temp中,并将对应指针向后移动一位。最后将临时数组temp中的元素复制回原数组arr中,完成排序。
图片: