【图论】无向图连通性(tarjan算法)
割边:dfn[u]<low[v]
割点:dfn[u]<=low[v] (若为根节点,要有两个v这样的点)
一.知识点:
1.连通:
在图论中,连通性是指一个无向图中的任意两个顶点之间存在路径。如果对于图中的任意两个顶点 u 和 v,存在一条路径从 u 到 v,那么图被称为连通图。如果图不是连通的,那么它可以被分为多个连通分量,每个连通分量都是一个连通子图。
2.割点:
割点(Cut Vertex),也称为关节点或割顶,是指在无向图中,如果移除该顶点及其相连的边,会导致图不再连通,那么该顶点就被称为割点。
3.割边:
割边(Cut Edge),也称为桥,是指在无向图中,如果移除该边,会导致图不再连通,那么该边就被称为割边。
割边在图中起到了连接不同连通分量的作用,其移除会导致图的连通性发生变化。
4.tarjan算法:(选择性阅读)
![]()
Tarjan算法是一种用于寻找有向图中强连通分量(Strongly Connected Components,简称SCC)的算法,由Robert Tarjan在1972年提出。强连通分量是指在有向图中,任意两个顶点之间存在双向路径。
Tarjan算法使用深度优先搜索(DFS)来遍历图,并通过维护一个栈和一些辅助数据结构来识别强连通分量。算法的基本思想是通过DFS遍历图中的每个顶点,并为每个顶点记录其访问次序(Discovery Time)和能够回溯到的最早的祖先顶点(Lowest Ancestor)。通过这些信息,可以识别出具有相同祖先的顶点集合,即一个强连通分量。
Tarjan算法的步骤如下:
- 对图中的每个顶点进行深度优先搜索(DFS)遍历。
- 在DFS遍历的过程中,为每个顶点记录其访问次序和最早祖先顶点。
- 将已访问的顶点入栈。
- 当DFS遍历回溯到一个顶点时,检查该顶点的最早祖先顶点。如果最早祖先顶点是自身,则将栈中的顶点弹出,并将这些顶点构成一个强连通分量。
- 重复步骤3和步骤4,直到遍历完所有的顶点。
Tarjan算法的时间复杂度为O(V+E),其中V是顶点数,E是边数。它是一种高效的算法,常被用于解决与强连通分量相关的问题,如图的缩点、强连通分量的数量和结构等。
总之,Tarjan算法是一种用于寻找有向图中强连通分量的算法,通过DFS遍历和栈的运用,可以高效地找到图中的所有强连通分量。
二.讲解
在此之前,先介绍两个数组;
int dfn[];里面存放访问顺序(时间戳);
int low[];里面存放追溯值(即祖先节点最小的dfn)
(1)割边
tarjan提出:(证明可以自行百度)
当dfn[u]<low[v]时,连接这两条点的边为割边(重边要特殊处理,后面介绍)
(2)割点
tarjan提出:(证明可以自行百度)
当dfn[u]<=low[v]时,u这个点为割点(若为根节点,要有两个v这样符合条件的点)
三.割边
(1)题目
题目描述:
找出割边
输入:
第一行输入两个整数n和m,表示点和边的个数。
第i(2<=i<=2+m)行,每行输出两个数字,表示一条边的两个点。
输出:
割边
样例输入:
6 7
1 2
1 3
2 4
2 5
3 4
4 5
4 6样例输出:
4---6
(2)初代码
/*
6 7
1 2
1 3
2 4
2 5
3 4
4 5
4 6
*/#include<bits/stdc++.h>
#define maxn 100005
using namespace std;
int n,m;
struct Edge{int u,v,next;
}edge[maxn<<1];
int cnt,head[maxn];
void add(int u,int v){edge[++cnt]=(Edge){u,v,head[u]}; head[u]=cnt;
}
int num,dfn[maxn],low[maxn];
void tarjan(int u,int fa){dfn[u]=low[u]=++num;for(int i=head[u];i;i=edge[i].next){int v=edge[i].v;if(v==fa) continue;if(dfn[v]==0){tarjan(v,u);low[u]=min(low[u],low[v]);if(dfn[u]<low[v]){ //割边条件 ,若>则表示v不止和u相连 cout<<u<<"----"<<v<<endl; }}else{low[u]=min(low[u],dfn[v]);}}
}
int main(){scanf("%d%d",&n,&m);int u,v;for(int i=1;i<=m;i++){scanf("%d%d",&u,&v);add(u,v); add(v,u);}tarjan(1,0);return 0;
}(3)bug与解答
1.若这张图有多个连通分量怎么办?
答:遍历即可
for(int i=1;i<=n;i++){if(dfn[i]==0) tarjan(1,0);}2.若有重边怎么办?结果显然不对。
答:只continue,第二次让这段代码运行
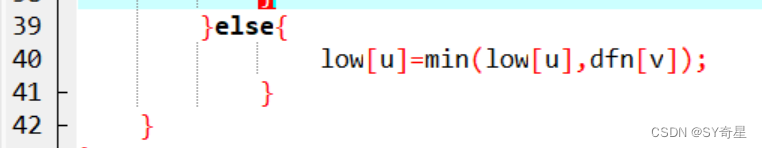
然后就无法满足 dfn[u]<low[v]条件了
if(v==fa){k++; //防止重边 if(k==1) continue;} (4)最终代码
/*
6 7
1 2
1 3
2 4
2 5
3 4
4 5
4 6
*/#include<bits/stdc++.h>
#define maxn 100005
using namespace std;
int n,m;
struct Edge{int u,v,next;
}edge[maxn<<1];
int cnt,head[maxn];
void add(int u,int v){edge[++cnt]=(Edge){u,v,head[u]}; head[u]=cnt;
}
int num,dfn[maxn],low[maxn];
void tarjan(int u,int fa){int k=0;dfn[u]=low[u]=++num;for(int i=head[u];i;i=edge[i].next){int v=edge[i].v;if(v==fa){k++; //防止重边 if(k==1) continue;} if(dfn[v]==0){tarjan(v,u);low[u]=min(low[u],low[v]);if(dfn[u]<low[v]){ //割边条件 ,若>则表示v不止和u相连 cout<<u<<"---"<<v<<endl; }}else{low[u]=min(low[u],dfn[v]);}}
}
int main(){scanf("%d%d",&n,&m);int u,v;for(int i=1;i<=m;i++){scanf("%d%d",&u,&v);add(u,v); add(v,u);}//防止本来就有不连通的 for(int i=1;i<=n;i++){if(dfn[i]==0) tarjan(1,0);}return 0;
}四.割点
其实只是微改动一下即可。其次就是可以优化一下。函数传参只需要传u,无需判断是否为父节点。因为不会影响结果。(自行参考代码推理)
再次强调:若为根节点,要有两个v这样的点!
参考代码:
/*
6 7
1 2
1 3
2 4
2 5
3 4
4 5
4 6
*/#include<bits/stdc++.h>
#define maxn 100005
using namespace std;
int n,m;
struct Edge{int u,v,next;
}edge[maxn<<1];
int cnt,head[maxn];
void add(int u,int v){edge[++cnt]=(Edge){u,v,head[u]}; head[u]=cnt;
}
int num,dfn[maxn],low[maxn],root;
void tarjan(int u){dfn[u]=low[u]=++num;int flag=0;for(int i=head[u];i;i=edge[i].next){int v=edge[i].v;if(dfn[v]==0){tarjan(v);low[u]=min(low[u],low[v]);if(dfn[u]<=low[v]){ //割点条件 if(u!=root || flag>1) cout<<u<<" ";}}else{low[u]=min(low[u],dfn[v]);}}
}
int main(){scanf("%d%d",&n,&m);int u,v;for(int i=1;i<=m;i++){scanf("%d%d",&u,&v);add(u,v); add(v,u);}//防止本来就有不连通的 for(int i=1;i<=n;i++){if(dfn[i]==0){root=i;tarjan(i);} }return 0;
}