拿捏--->求一元二次方程的根
文章目录
- 题目描述
- 算法思路
- 代码示例
题目描述
从键盘输入a, b, c的值,编程计算并输出一元二次方程ax2 + bx + c = 0的根,当a = 0时,输出“Not quadratic equation”,当a ≠ 0时,根据△ = b2 - 4ac的三种情况计算并输出方程的根。
输入描述:
多组输入,一行,包含三个浮点数a, b, c,以一个空格分隔,表示一元二次方程ax2 + bx + c = 0的系数。
输出描述:
针对每组输入,输出一行,输出一元二次方程ax2 + bx +c = 0的根的情况。
如果a = 0,输出“Not quadratic equation”;
如果a ≠ 0,分三种情况:
△ = 0,则两个实根相等,输出形式为:x1=x2=…。
△ > 0,则两个实根不等,输出形式为:x1=…;x2=…,其中x1 <= x2。
△ < 0,则有两个虚根,则输出:x1=实部-虚部i;x2=实部+虚部i,即x1的虚部系数小于等于x2的虚部系数,实部为0时不可省略。实部= -b / (2a),虚部= sqrt(-△ ) / (2a)所有实数部分要求精确到小数点后2位,数字、符号之间没有空格。
算法思路
要想使用c语言编写这个实例,就需要知道数学上的公式。
一元二次方程表达式为:a * x * x + bx + c = 0(其中,a ≠ 0)
根的判别式为:Δ = b * b - 4 * a * c;
求根公式为:
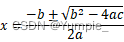
手动输入三个系数,分别代表二次项系数、一次项系数、常数项;
判断输入的二次项系数是否为0,如果为0,提示“输入的第一个值不合法,请重新输入!”;
如果二次项系数不为0,利用根的判别式,计算一元二次方程是否有根;
如果判别式 Δ >= 0 ,代表方程有两个根,输出根;
如果 Δ < 0 ,提示“方程无根”。
代码示例
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<math.h>
int main()
{float a, b, c;while (scanf("%f %f %f", &a, &b, &c) != EOF){double dt = pow(b, 2) - 4 * a * c;if (a == 0){printf("Not quadratic equation");}else{if (dt == 0)//△=0{double x1 = (-b - sqrt(dt)) / (2 * a);double x2 = (-b + sqrt(dt)) / (2 * a);printf("x1=x2=%.2f", x1);}else if (dt > 0)//△>0{double x1 = (-b - sqrt(dt)) / (2 * a);double x2 = (-b + sqrt(dt)) / (2 * a);printf("x1=%.2f;x2=%.2f", x1, x2);}else//△<0{double real = (-b) / (2 * a);//实部double imaginary = sqrt(-dt) / (2 * a);//虚部printf("x1=%.2f-%.2fi;x2=%.2f+%.2fi", real, imaginary, real, imaginary);}}printf("\n");}return 0;
}