647. 回文子串

https://leetcode.cn/problems/palindromic-substrings/solution/by-lfool-2mvg/

Given a string s, return the number of palindromic substrings in it.
A string is a palindrome when it reads the same backward as forward.
A substring is a contiguous sequence of characters within the string.

dp[i][j] 表示子串 [i…j] 是否为回文子串

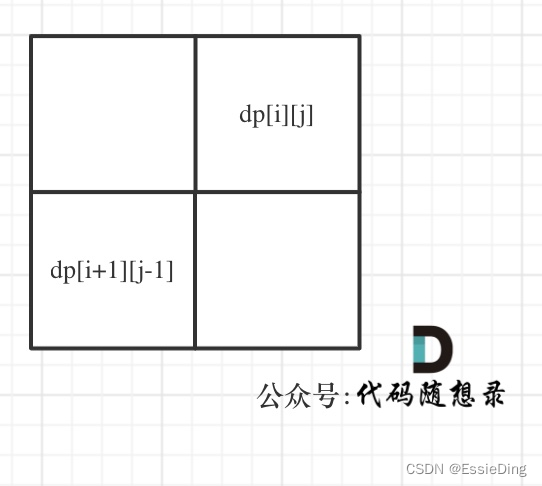
当我们判断 [i…j] 是否为回文子串时，只需要判断 s[i] == s[j]，同时判断 [i-1…j-1] 是否为回文子串即可

需要注意有两种特殊情况：[i, i] or [i, i + 1]，即：子串长度为 1(s = “a”) 或者 2 (s = “aa”)。所以加了一个条件限定 j - i < 2

状态转移方程如下：

dp[i][j] = (s[i] == s[j]) && (j - i < 2 || dp[i + 1][j - 1])

初始化默认为不匹配，false。

这里注意遍历顺序，因为dp[i][j]是由dp[i+1][j-1]来判断是不是回文子串，所以i应当从大到小，j从小到大。
所以一定要从下到上，从左到右遍历，这样保证dp[i + 1][j - 1]都是经过计算的。

class Solution {public int countSubstrings(String s) {boolean[][] dp = new boolean[s.length()][s.length()];int res = 0;for (int i = s.length()-1; i >= 0; i--) {for (int j = i; j < s.length(); j++) {if (s.charAt(i) == s.charAt(j)) {if (j < i+2 || dp[i+1][j-1]) {dp[i][j] = true;res++;}}}}return res;}
}

class Solution {public int countSubstrings(String s) {boolean[][] dp = new boolean[s.length()][s.length()];int res = 0;for (int j = 0; j < s.length(); j++) {for (int i = j; i >= 0; i--) {if (s.charAt(i) == s.charAt(j)) {if (j < i+2 || dp[i+1][j-1]) {dp[i][j] = true;res++;}}}}return res;}
}

中心扩散法
center expansion

private int ans = 0;
public int countSubstrings(String s) {for (int i = 0; i < s.length(); i++) {// 以单个字母为中心的情况isPalindromic(s, i, i);// 以两个字母为中心的情况isPalindromic(s, i, i + 1);}return ans;
}
private void isPalindromic(String s, int i, int j) {while (i >= 0 && j < s.length()) {if (s.charAt(i) != s.charAt(j)) return ;i--;j++;ans++;}
}

516.最长回文子序列

https://leetcode.cn/problems/longest-palindromic-subsequence/solution/zi-xu-lie-wen-ti-tong-yong-si-lu-zui-chang-hui-wen/

Given a string s, find the longest palindromic subsequence’s length in s.
A subsequence is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements.

Input: s = “bbbab”
Output: 4
Explanation: One possible longest palindromic subsequence is “bbbb”.

注意区分子串和子序列：
回文子串是要连续的，回文子序列可不是连续的！

在子串 s[i…j] 中，最长回文子序列的长度为 dp[i][j]。

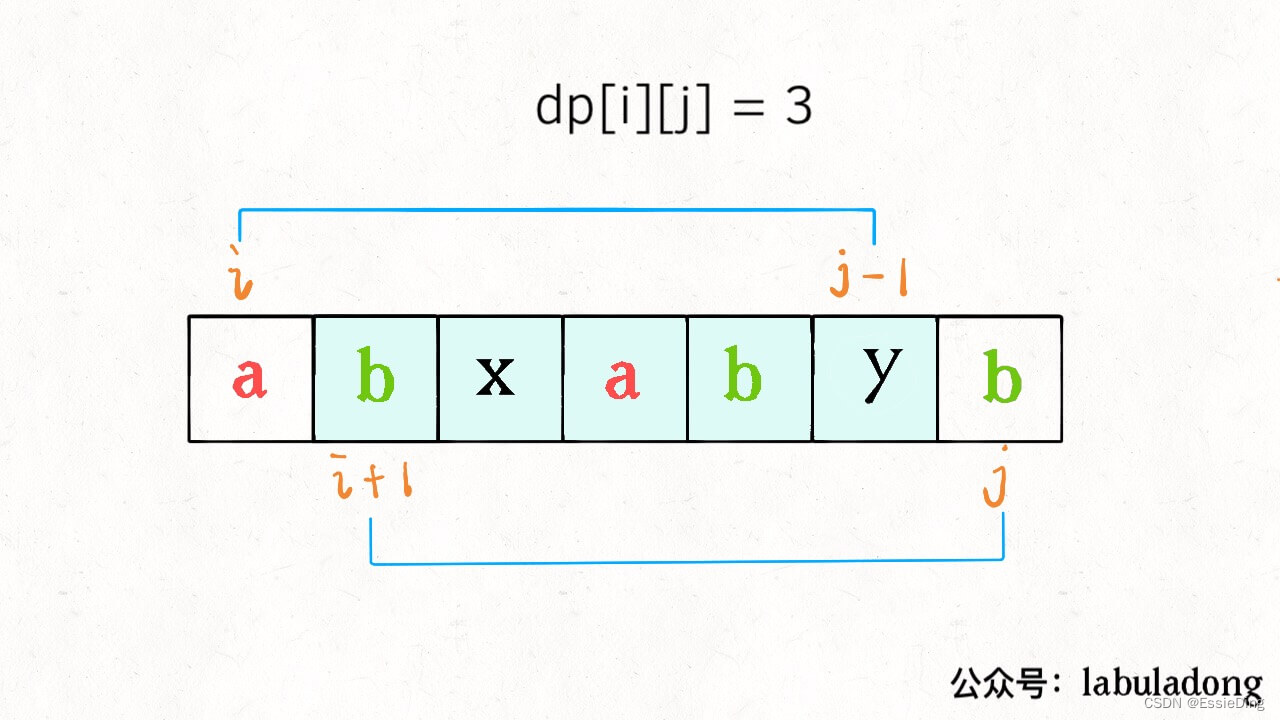
求dp[i][j], 假设已知子问题dp[i+1][j-1]的值，
只要s[i] = s[j]，那么它俩加上 s[i+1…j-1] 中的最长回文子序列就是 s[i…j] 的最长回文子序列。
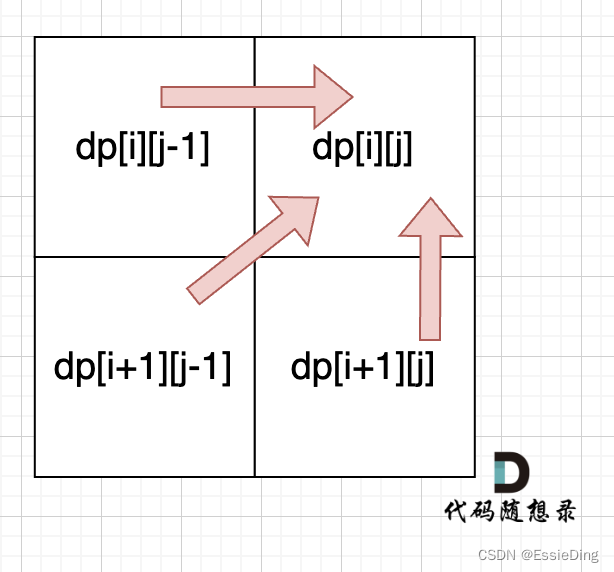
如果s[i]与s[j]不相同，说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子序列的长度，
或者说如果 s[i] ≠ s[j]，则 s[i] 和 s[j] 不可能同时作为同一个回文子序列的首尾，
那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。

遍历顺序：必须从下到上，从左到右

class Solution {public int longestPalindromeSubseq(String s) {int[][] dp = new int[s.length()][s.length()];for (int i = 0; i < s.length(); i++) {dp[i][i] = 1;}for (int i = s.length()-1; i >= 0; i--) {for (int j = i+1; j < s.length(); j++) {if (s.charAt(i) == s.charAt(j)) {dp[i][j] = dp[i+1][j-1] + 2;} else {dp[i][j] = Math.max(dp[i+1][j], dp[i][j-1]);}}}return dp[0][s.length()-1];}
}

class Solution {public int longestPalindromeSubseq(String s) {int[][] dp = new int[s.length()][s.length()];for (int i = s.length()-1; i >= 0; i--) {for (int j = i; j < s.length(); j++) {if (s.charAt(i) == s.charAt(j)) {if (i == j){dp[i][j] = 1;} else {dp[i][j] = dp[i+1][j-1] + 2;}} else {dp[i][j] = Math.max(dp[i+1][j], dp[i][j-1]);}}}return dp[0][s.length()-1];}
}