双目立体视觉:SAD算法
算法原理
SAD(Sum of absolute differences)是一种图像匹配算法。基本思想:差的绝对值之和。此算法常用于图像块匹配,将每个像素对应数值之差的绝对值求和,据此评估两个图像块的相似度。该算法快速、但并不精确,通常用于多级处理的初步筛选。
常见立体匹配算法流程
常见的立体匹配算法主要包括以下四步
匹配代价计算
代价聚合
视差计算或优化
视差改良
匹配代价计算常采用sad等方法,根据左右两幅图像上匹配点的像素之差的绝对值。
代价聚合常采用一个固定窗口,计算窗口内部的所有视差之和。
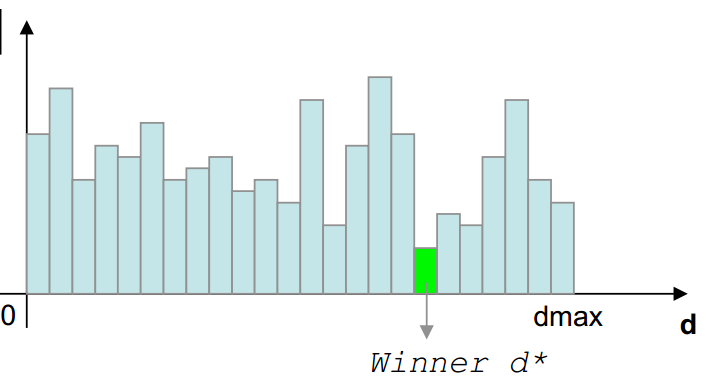
视差的计算最直观的方式是采用WTA(Winner Takes All)的方式,直接选取使得聚合代价最小的视差值。
BM算法概括
简单的理解立体匹配,在行对准的两幅图像中找到同一个点,或Reference图像中给定一点,在Target图像中搜索对应的点,如下图所示。

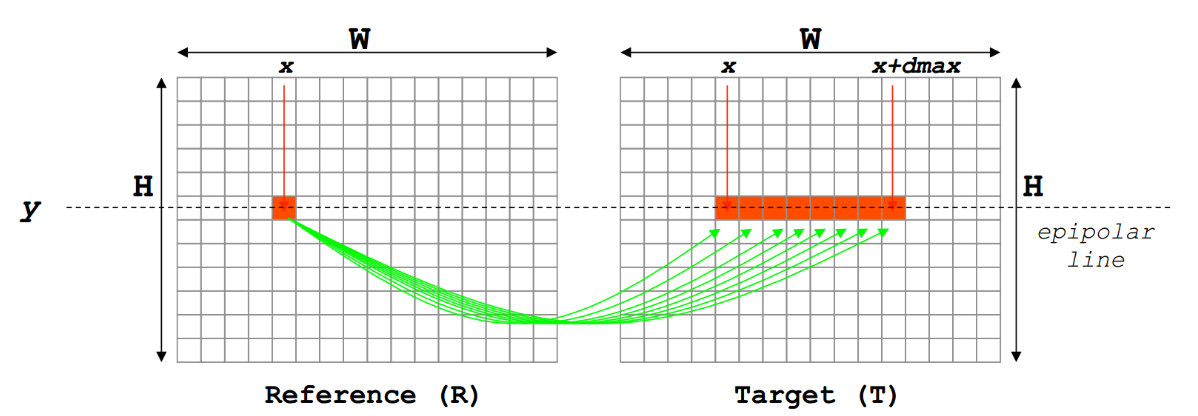
根据极线规则,上图左边图中红色像素点(x, y)到右边图中搜索匹配点。实际上,直接对一点来进行匹配,百分百会出现各种各样的问题,这个时候我们选择用一个固定窗口来替代一点,如下图所示。

这样做就隐含了一个假设,认为窗口内部视差值相同,但是,显然的,这种假设太过想当然,也使得算法实际效果不好。
BM算法,也常称为SAD(Sum of Absolute Differences)算法,是双目立体匹配中最基本的算法。
SAD基本理论
SAD算法由3步构成。
匹配代价计算
代价聚合
视差计算
Matching Cost Computation
SAD的匹配代价计算比较简单,Reference图像和Target图像像素直接相减加绝对值,即|IR(x,y)−IT(x+d,y)||IR(x,y)−IT(x+d,y)|。
视差空间(DSI)是一个三维矩阵,定义
[c(x,y,d)= | I_R(x,y)-I_T(x+d,y) | ] |
可以理解为Reference图像(x,y)(x,y)点,在搜索视差为dd时的代价。
Cost Aggeration
SAD的代价聚合就是将固定窗口FW(Fixed Window)内代价求和,直观理解如下图所示。

计算FW内视差视差为d时的聚合代价
[C(x,y,d)=\sum_{x\in S}|I_R(x,y)-I_T(x+d,y)|]
Disparity Computation
SAD的视差计算非常简单,采用WTA原则,对于给定的(x,y)(x,y),找使得C(x,y,d)C(x,y,d)最小的d,此d即可认为时该点的视差。
基本流程
输入:两幅图像,一幅Left-Image,一幅Right-Image且两幅图像已经校正实现行对准
对左图,依次扫描,选定一个锚点:
(1)设定SAD窗口的大小(下图灰色区域),left_image为开始匹配的位置,(p,q)以及在right_image中SAD窗口移动的范围D。
(2)在left_image图像中,确定待匹配的像素点的位置(x,y),并以此位置作为SAD窗口的锚点,用SAD窗口覆盖left_image中以(x,y)为锚点的区域regionl。
(3)在right_image图像中,选取匹配的开始点,位置为(m,n),并以该点作为SAD窗口的锚点,用SAD窗口去覆盖,在right_iamge中形成以(m,n)为锚点的图像区域regionr.
(4)定义differernce=regionr-regionl。计算difference中的和。
(5)在right_image图像中沿行方向移动SAD(移动次数为匹配的范围大小),重复步骤(3),(4),并将每次得到的difference记录在mat矩阵中。
(6)找到mat矩阵中difference最小的值,则其所在位置就是right_image和left_image的视差。

代码实现
#include "opencv2/opencv.hpp"class SAD
{
public:SAD() :winSize(7), DSR(30) {}SAD(int _winSize, int _DSR) :winSize(_winSize), DSR(_DSR) {}cv::Mat computerSAD(cv::Mat& L, cv::Mat& R); //计算SAD
private:int winSize; //卷积核的尺寸int DSR; //视差搜索范围};cv::Mat SAD::computerSAD(cv::Mat& L, cv::Mat& R)
{int Height = L.rows;int Width = L.cols;cv::Mat Kernel_L(cv::Size(winSize, winSize), CV_8U, cv::Scalar::all(0));cv::Mat Kernel_R(cv::Size(winSize, winSize), CV_8U, cv::Scalar::all(0));cv::Mat Disparity(Height, Width, CV_8U, cv::Scalar(0)); //视差图for (int i = 0; i < Width - winSize; i++){for (int j = 0; j < Height - winSize; j++){Kernel_L = L(cv::Rect(i, j, winSize, winSize));cv::Mat MM(1, DSR, CV_32F, cv::Scalar(0)); //MM是一个1行DSR列的图像(矩阵)for (int k = 0; k < DSR; k++){int x = i - k; //为什么是i-k参见我上面的叙述if (x >= 0){Kernel_R = R(cv::Rect(x, j, winSize, winSize));cv::Mat Dif;cv::absdiff(Kernel_L, Kernel_R, Dif);//cv::Scalar ADD = sum(Dif);float a = ADD[0];//a为视差为k是相应窗口的像素差值的绝对值之和MM.at<float>(k) = a;//将a赋给MM的第k列,因为从0开始搜索,遍历结束后MM每一列为视差为列序号时对应的SAD值,我们取其最小即可std::cout << "i,j: " << i << ", " << j << "; MM " << MM << std::endl;}}cv::Point minLoc; //point数据类型为二维点对象,有横纵xy两个坐标double min = 0.0;cv::minMaxLoc(MM, &min, NULL, &minLoc, NULL);//返回MM最小值的坐标int loc = minLoc.x;//取最小值坐标的横坐标x值,即为对应的列序号,也就是相应的视差值//int loc=DSR-loc;Disparity.at<char>(j, i) = loc * 16;//*16只是为了方便显示}double rate = double(i) / (Width);//cout << "已完成" << setprecision(2) << rate * 100 << "%" << endl; //处理进度}return Disparity;
}int main()
{cv::Mat Img_L = cv::imread("SAD\\left_0.jpg", 0);cv::Mat Img_R = cv::imread("SAD\\right_0.jpg", 0);cv::Mat Disparity; //视差图//SAD mySAD;SAD mySAD(7, 30);Disparity = mySAD.computerSAD(Img_L, Img_R);cv::imshow("Img_L", Img_L);cv::imshow("Img_R", Img_R);cv::imshow("Disparity", Disparity);cv::waitKey();return -1;
}备注:
用SAD算法可以得出左右图像的视差,进一步处理就可以得到深度图,深度与视差成反比的关系。我们做个实验:将手指头放在离眼睛不同距离的位置,并轮换睁、闭左右眼,可以发现手指在不同距离的位置,视觉差也不同,且距离越近,视差越大,其中距离的远近就是深度了。并且可以观察到,用左眼看手指时,手指在你眼中的靠右位置,而用右眼看时,手指在你眼中靠左的位置。假设两只眼分别看到的视野一样大。若用(x,y)表示左眼视图中某个位置的坐标,那么相应的该位置右眼视图的坐标应该为(x-d,y),其中d就是视差。这时(x,y)和(x-d,y)就是最佳匹配点。但是实际情况我们并不知道d是多少。SAD算法就给出了如何求视差d.
SAD算法:我们按视差搜索范围从0开始搜索,找到左右图像最匹配的点,对应的视差值就确定了。如何确定最佳匹配点呢?试想一下,如果视差为0,也就是左右图像一样,那么这个点上下左右区域对应的点都应该相同,所以像素相减后都为0,由于视差的存在(简单理解为从不同的角度看物体,由于光照的影响像素值也会发生改变),该点上下左右区域的像素值不会完全相等,但是我们依然可以利用这个思想,设定一个小窗口,在左右两幅图中计算其像素值差的绝对值之和。根据极线约束覆盖右图像像素点,假如视差搜索范围为0-50,那么就会得到51个结果。若在某个视差值d下该绝对值之和最小,那么d就为该中心点对应的视差。再由视差与深度的关系就可以得到深度图。
https://jiweibo.github.io/StereoBM/
