约瑟夫环问题(队列,链表实现)- c++
1.关于约瑟夫问题
约瑟夫斯领导犹太人反抗罗马帝国的统治,在与罗马军队的激烈战斗中,与士兵们一同被困在一个山洞里。总共有41人,约瑟夫斯希望向罗马军队投降,但他的士兵们却坚决拒绝,宁愿死也不愿被敌人俘虏。面对这种困境,约瑟夫斯需要找到一种既能实现投降目的,又能确保自己安全的解决方案。
于是,他提出了一个方案:让大家围成一个圈,按照顺时针的顺序,每数到第m个人就杀掉,这个过程不断重复,直到最后只剩下一个人。这样,通过数学计算和策略安排,约瑟夫斯能够确保自己不被处决,同时实现投降的目的。士兵们接受了这个方案,并按照约瑟夫斯的要求行动起来。
例如,有7个人围成一圈,按顺序编号,约定数到3的人自杀,那么顺序如下:
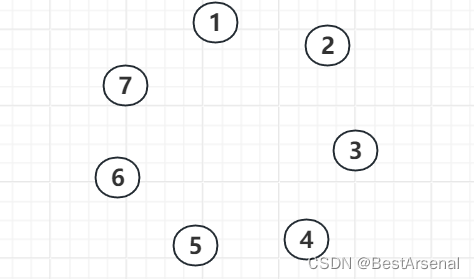
第一次报数: 3号被淘汰。
第二次报数: 6号被淘汰。
第三次报数: 2号被淘汰。
第四次报数: 7号被淘汰。
第五次报数: 5号被淘汰。
第六次报数: 1号被淘汰。
最后存活的十是4号。
2.题目描述
对于给定的n和m,分别表示总人数和要报的数字,求最后剩余的人是几号?
输入:7 3
输出:4
3.算法1 (队列实现)
思考报数过程,其报数规律如下:
1 2 3 4 5 6 7 (3应该被淘汰,接下来的报数顺序应该是如下)4 5 6 7 1 2 (数到7后继续从1开始,模拟环,此时6应该被淘汰,变成)7 1 2 4 5 (同上,接下来2该被删除,变成)4 5 7 1 (7被删除)1 4 5 (5被删除)1 4 (1被删除)4 //即存活的人
可以发现,数字顺序的变化规律,就是将报到m之前的人(m-1)移到最后面来模拟环,之后再删除要删除的数即可。在数列的前面进行删除操作,在数列后面进行删除操作,故可以采用队列这种数据结构。
实现函数如下:
/* 队列求解 */
int getAnsByQueue(int n,int m){queue<int> q;for(int i