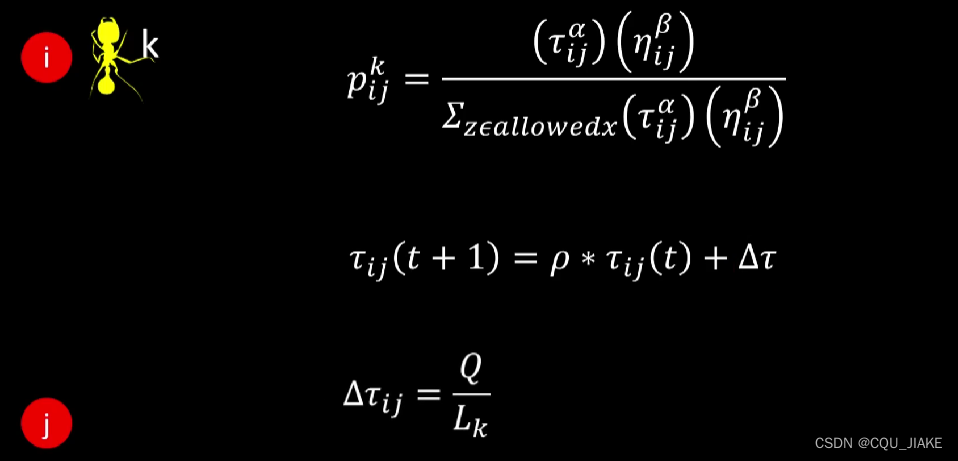1.23聚类算法（kmeans(初始随机选k，迭代收敛）,DBSCAN（dij选点），MEANSHIFT（质心收敛），AGENS(最小生成树）），蚁群算法（参数理解、过程理解、伪代码、代码）

聚类算法 

聚类结果不变

K-means 

K值是事先确定好的，是要划分的聚类的数量；初始时随机选择k个点，然后逐渐选择离他最近的点，不断锁定最近的，最后计算方差和；这个是轮流的

这个就类似于模拟退火的思想

当前聚类下的方差和，也称为簇内方差（within-cluster variance），是一种度量聚类质量的指标。它衡量了簇内数据点与各自簇中心的差异程度。方差和越小，表示簇内的数据点越紧密聚集在一起。

计算当前聚类下的方差和的一种常见方法是使用平方欧氏距离（squared Euclidean distance）。具体计算步骤如下：

1. 对于每个簇，计算该簇内所有数据点与簇中心的平方欧氏距离。
2. 将每个簇内所有数据点与簇中心的平方欧氏距离求和。
3. 将所有簇的平方欧氏距离之和作为当前聚类下的方差和。

简化的计算公式如下：

方差和 = Σ(Σ(欧氏距离^2))

其中，Σ表示求和操作，欧氏距离^2表示欧氏距离的平方。

需要注意的是，方差和的计算可能因聚类算法而异，所以在具体应用中，请参考所使用的聚类算法的文档或相关资料，了解更准确的计算方法。

要确定K值，采用肘方法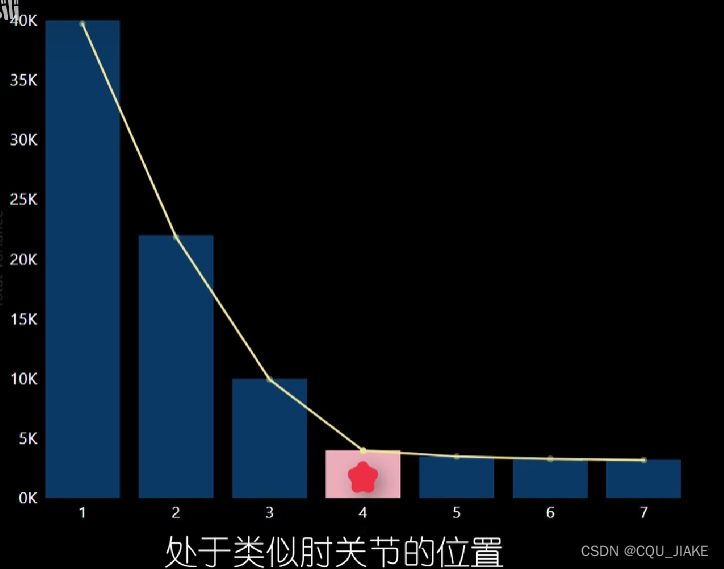

 

DBSCAN

 带噪声的聚类

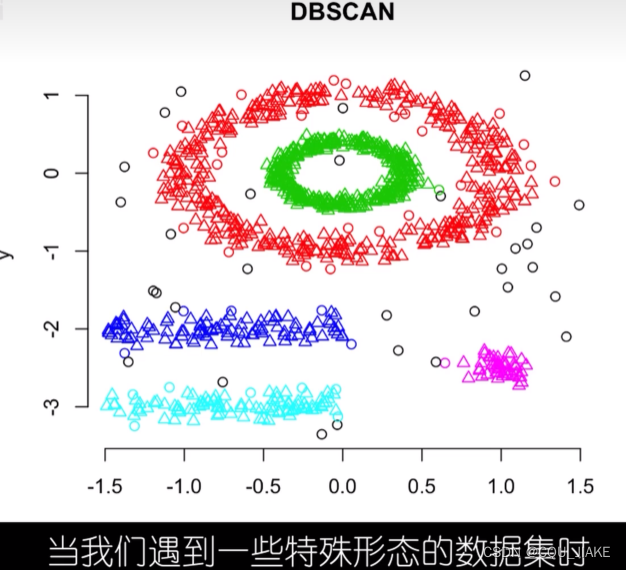
两个参数

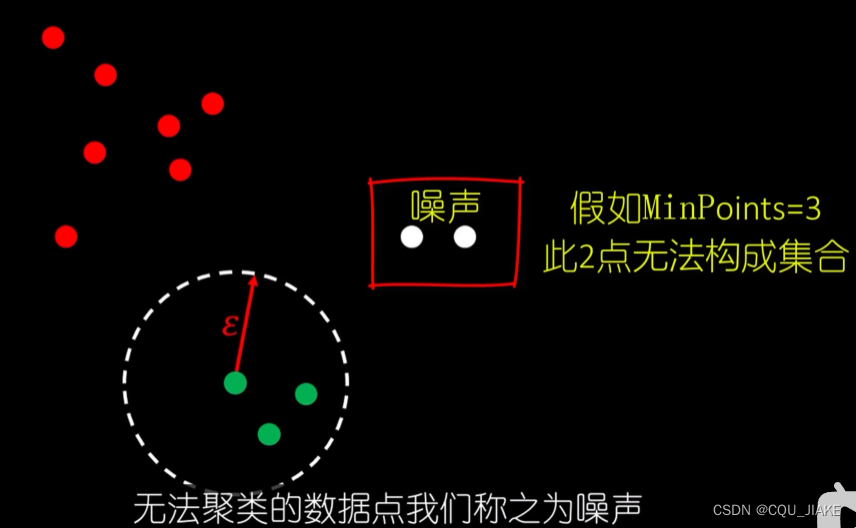
一个是距离参数，一个是最少点数；就是先从某点（随机点）出现，然后以这个点为圆心向周围辐射，辐射大小是距离参数，之后再以确定的点去确定其他点，就是dij的一个过程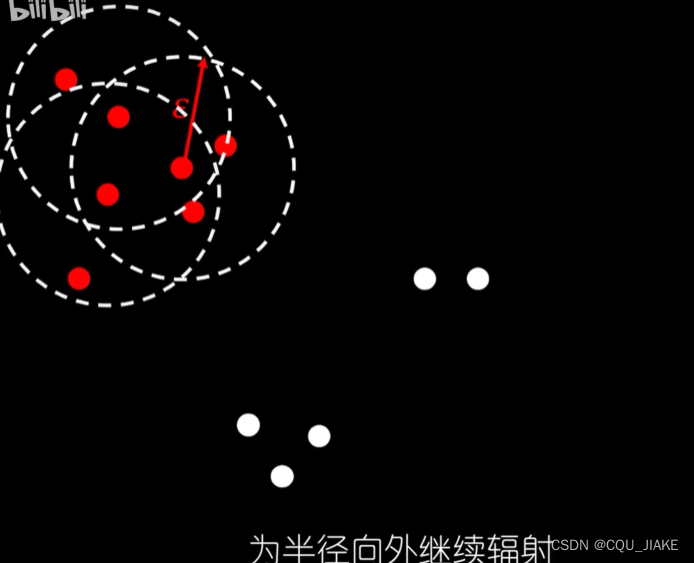

MEANSHIFT均值漂移算法 

先选一个半径为r的分析区域， 计算质心，然后以质心为圆心再计算，迭代一定次数后最终趋向于最终最密集的地方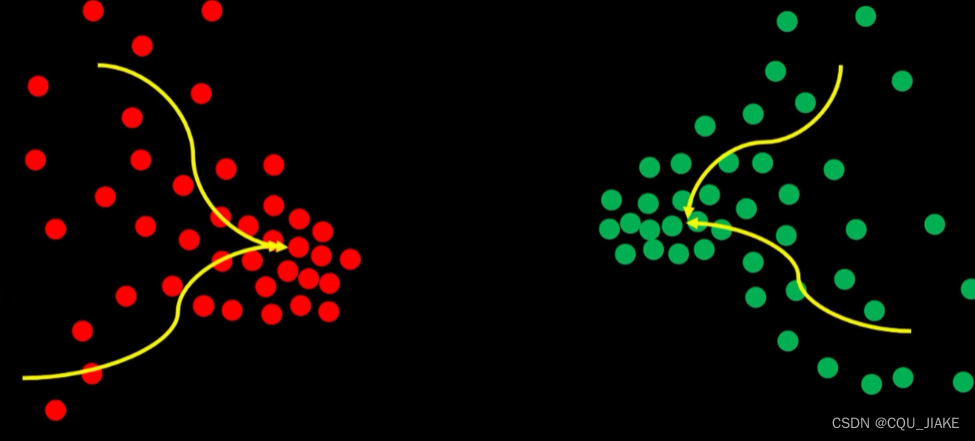

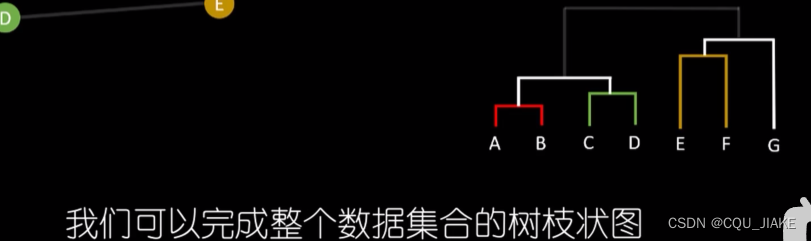
AGNES集聚分层聚类算法

能保证最近的两点归于同一组

纵坐标为对应的聚类距离临界值

就是相当于最小生成树的p算法，只不过在相连的时候，如果边的权值大于聚类距离临界值了，就不练了，就作为新的聚类连通图。重复这个过程直到所有点

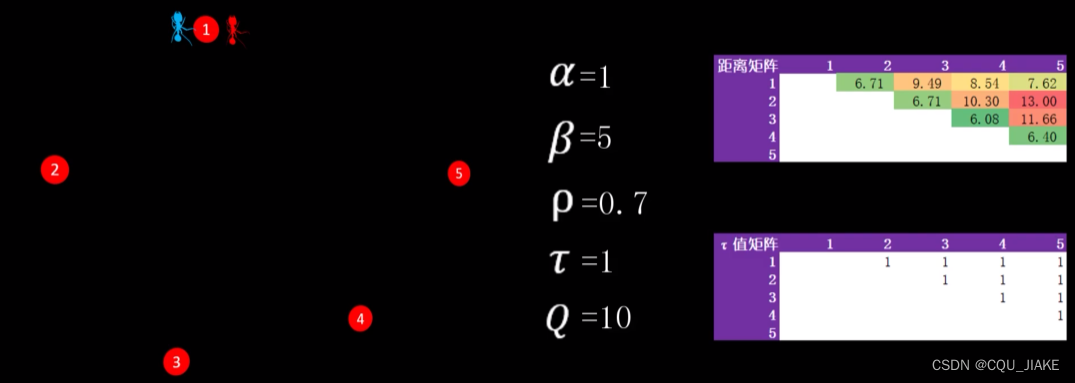
 最优路径问题，蚁群ACO

三个参数，阿尔法，β，挥发系数ρ值