计算机组成原理-检错码、纠错码

1.纠错码有什么作用

• 由于电源的尖峰电压或其他原因，计算机主存的数据在传输的过程中偶尔也会出错。为了防止这些错误产生不良后果，我们在主存中采用检错和纠错的方式来处理错误。

2.主要概念

**码字：m位数据位和r位校验位组成的n个位单元称为n位码字

**海明码距：两个码字间不同的位数的个数

 值得注意的是，当存在很多码字的时候，我们将这些码字看作是一个集合，该集合的海明码距的值就是其中任意两个码字产生的最小的海明码距。

3.检错、纠错

检错：检查d位错误，编码的码距要d+1位。 Why?
纠错：纠正d位错误，编码的码距要2d+1位 。 Why?

(解释上面的两个Why）用图示的方法理解检错能力、纠错能力与码距之间的关系

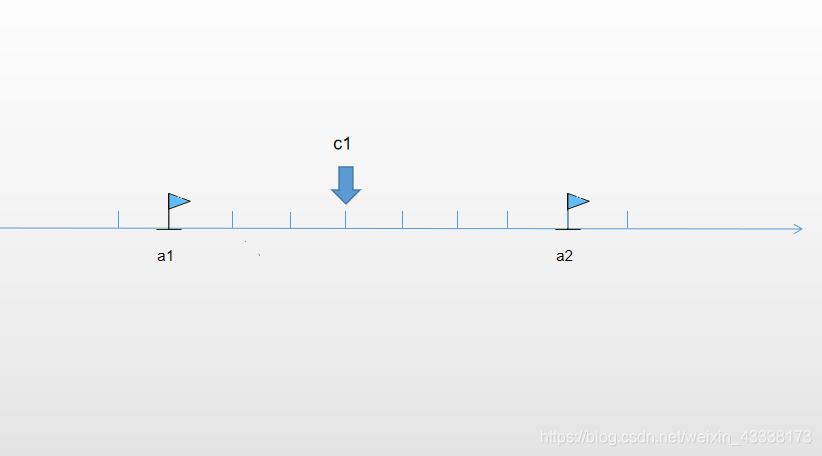
• 如图，a₁和a₂代表合法的码字，它们之间的距离代表了它们的海明码距，所以说当海明码距为d时任何小于d位的错误都不会使之前的码字变成一个合法码字，因此可以用这种原理判断是否出错(如果出错的位数不小于d的时候，一个合法码字会变成另一个合法码字，这种错误会被当做未出错来处理)。同样的道理，为了使码字出错之后还可以纠正，我们可以通过将错误码字修改成最“近”的合法码字的方法来纠正错误。如图中的c₁，我们可以推断出这个错误的码字更有可能是从合法码字a1发生错误而产生的，所以我们将错误码字c₁修改成a₁来纠正错误。因此我们就要保证海明码距的大小至少是需要纠正的位数的2倍还多出1.
• 因此总的来说码距越大，检错的和纠错的能力也就越强。

4.举例说明

**奇偶校验：

• 一位的奇偶校验：给数据位添加一个bit的奇偶校验位的校验码被称为奇偶校验。根据原数据位中1的位数是奇数或是偶数来设置奇偶校验位是0或1。
• 奇偶校验是海明码距为2的校验法，也就是说任意一个合法码字两个bit位出现错误就会变成另一个合法码字。
• 如， 11010101，对它进行奇校验，变成011010101（校验位添加在了最前面，以保证1的个数是奇数个），当它的任意一个位发生改变时，便会导致1的个数变成了偶数而引发错误。
• 因此，通过上面的分析可以知道奇偶校验是一种具有一位错误检错能力的校验码(因为2-1 = 1),但是奇偶校验没有纠错能力(因为(2-1)/2 = 0.5, 0.5 < 1,所以说连一位错误都没办法纠正)。

5.一般性方法（这描述的是一种推广，如何通过增加码距来使设计方案获得更好的检错、纠错能力？）

如何构造一个可以纠正(不是检测)m位数据位中至多有d位错误的校验码呢？这种校验码至少需要多少个校验位呢？

• m位数据位就存在2^m个合法码字，假设需要r位校验位，则总共有n = m + r个位。由于校验位的取值是由数据位直接决定的而且唯一对应（这是一个好的校验算法必须要做到的事情），所以2ⁿ个码字中只有2^m个合法码字。
• 其次，在纠错码的应用中通常有多个错误码字对应同一个合法的码字(使用上面的图来说明就是a₁和a₂都对应这三个错误码)，一般情况会是多少个呢？我们尝试着去想，可能是1位错、2位错、3位错、、、d位错（因为我们可以纠正到d位，d也可以是1、2或3），所以总共会有${\sum }_{k=1}^d{C}_n^k$个错误的码字与一个合法的码字对应（这里的$C_n^k$是确保错误发生的随机性，计算k个错误发生在n个位置的所有可能性）。为了加上一个合法码字可将公式改写为${\sum }_{k=0}^d{C}_n^k$，该公式表明一个合合法码字所对应的所有码字，因为总共有2^m个合法码字，所以总共有2^m${\sum }_{k=0}^d{C}_n^k$个不同的码字。
• 我们现在只要保证n位的纠错码能够表示上述所说的所有不同的码字就行，即得到不等式
  $$2^m\sum _{k=0}^d{C}_n^k\le 2^n$$
  解这个不等式就能构求出n的最小值，从而求出r的最小值。

使用该公式求当要求纠正1（即公式中k取1）位错误时所需要的校验位的个数

数据位数m	需要的校验位r	总长n	校验位与数据位之比(%)
8	4	12	50
16	5	21	31
32	6	38	19
64	7	71	11
128	8	136	6

能得到几个结论。第一，字长越长，校验位也需要变长。第二，字长越长，校验位在字长中的占比的百分比会变小。

**用相同的思想推出能检测出d位错误（不纠正，只发现错误）的检错码的推导不等式是
$$(2^m+1)\sum _{k=0}^{d-1}{C}_n^d+1\le 2^n$$
（该公式没有做系统的推导和证明仅做参考）