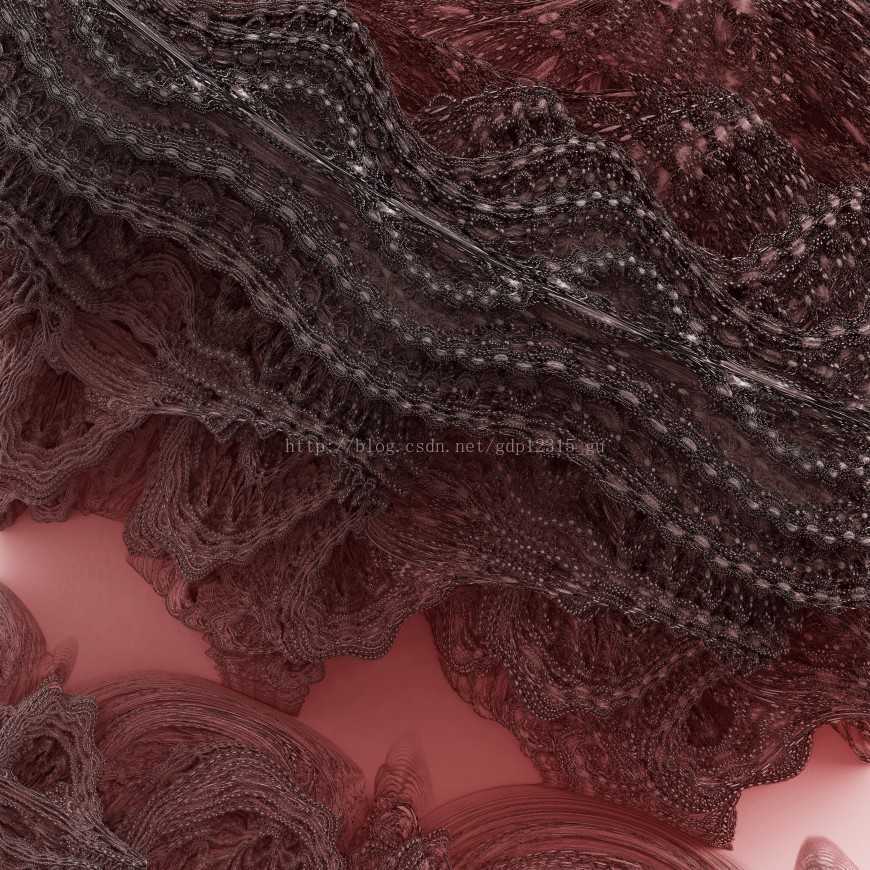
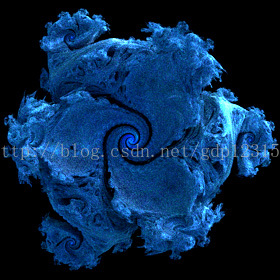
Mandelbrot集的最新变化形态一览——MandelBox,Mandelbulb,Burning Ship,NebulaBrot
二维Mandelbrot集——Burning Ship
采用以下迭代公式
(x4-6*x2*y2+y4,4*|x|3*|y|-4*|y|3*|x|)
看不懂的,可以去学习深造了。。。
Mandelbulb
这个3D的Mandelbrot集采用的是以下公式,这应该算是超复数的一种,人称“triplex”,三元复数
数学上的N次方
其中:
一般情况下,n取8。
简单说来,三元复数的平方的计算机表示为
xx = (x*x+y*y) * (1-z*z/(x*x+y*y));
yy = 2*x*y * (1-z*z/(x*x+y*y));
zz = -2*z*sqrt(x*x+y*y);
详情请参见http://en.wikipedia.org/wiki/Mandelbulb
以下内容摘自http://www.skytopia.com/project/fractal/2mandelbulb.html
{x,y,z}^n = r^n { sin(theta*n) * cos(phi*n) ,sin(theta*n) * sin(phi*n) , cos(theta*n) }
...where:
r = sqrt(x^2 + y^2 + z^2)
theta = atan2( sqrt(x^2+y^2), z )
phi = atan2(y,x)
And the addition term in z -> z^n + c is similar tostandard complex addition, and is simply defined by:
{x,y,z}+{a,b,c} = {x+a, y+b, z+c}
The rest of the algorithm is similar to the 2D Mandelbrot!
Here is some pseudo code of the above:
r = sqrt(x*x + y*y + z*z )
theta = atan2(sqrt(x*x + y*y) , z)
phi = atan2(y,x)
newx = r^n * sin(theta*n) * cos(phi*n)
newy = r^n * sin(theta*n) * sin(phi*n)
newz = r^n * cos(theta*n)
...where n is the order of the 3D Mandelbulb. Use n=8to find the exact object in this article.
上图是16阶的MandelbrotBulb
放大之后的某部分
取n=8时候的图形
迭代次数取100时候的情形
“金色大峡谷”
“神秘洞穴”
“魔法球花甘蓝”
“Mandelbrot花园”
八阶的MandelBulb
圣诞节珊瑚球
冰激凌~~
贝壳~~
“冰封地狱”
3D的Mandelbrot集——Mandelbox
一个很奇妙的视频演示。“飞越曼德布罗盒子”
http://wimp.com/mandelboxflythrough/
具体算法核心代码:
for (each axis)
if (v[axis]>1) v[axis] =2-v[axis];
else if (v[axis]<-1) v[axis] =-2-v[axis];
if (v.magnitude() < 0.5) v *= 4;
else if (v.magnitude() < 1) v /= square(v.magnitude());
v = scale*v + c;
详情参见“超复数分形”
http://www.bugman123.com/Hypercomplex/index.html
n = 100; norm[x_] := x.x;
TriplexPow[{x_, y_, z_}, n_] := If[x == y == 0.0, 0.0, Module[{r =Sqrt[x^2 + y^2 + z^2], theta = n ArcTan[x, y], phi}, phi = n ArcSin[z/r];
r^n{Cos[theta]Cos[phi], Sin[theta]Cos[phi], -Sin[phi]}]];
Mandelbulb[c_] := Module[{p = {0, 0, 0}, i = 0}, While[i < 24 &&norm[p] < 4, p = TriplexPow[p, 8] + c; i++]; i];
image = Table[z = 1.1; While[z >= -0.1 && Mandelbulb[{x, y, z}] <24, z -= 2.2/n];
z, {y, -1.1, 1.1, 2.2/n}, {x, -1.1, 1.1, 2.2/n}];
ListDensityPlot[image, Mesh -> False, Frame -> False, PlotRange ->{-0.1, 1.1}]
上图是Lambdabulb
上图所用迭代公式:{x,y,z}2 = {x2-y2-z2,2xy, -2xz}
上图是四元数Mandelbrot集,所用迭代公式:{x,y,z,w}2= {x2-y2-z2-w2, 2xy, 2xz, 2xw}
上图名叫Glynn Julia set
上面两幅图是4D Bicomplex Mandelbrot集("Tetrabrot")
所用迭代公式:{x,y,z,w}2 = {x2-y2-z2+w2,2(xy-zw), 2(xz-yw), 2(xw+yz)}
上面三幅图叫做NebulaBrot,是BuddhaBrot的三维形式
这些图均由20亿个点进行计算渲染而成
上图叫做3DChristmas Tree Mandelbrot Set,使用的迭代公式:
{x,y,z}n = rn{cos(θ)cos(φ),sin(θ)cos(φ), sin(φ)}
r=sqrt(x2+y2+z2), θ=n atan2(y,x), φ=natan2(z,x)
{x,y,z}n = rn{cos(θ)cos(φ),sin(θ)cos(φ), cos(θ)sin(φ)}
r=sqrt(x2+y2+z2), θ=n atan2(y,x), φ=n sin-1(z/r)
上图叫做"Roundy" Mandelbrot Set 。迭代公式:
{x,y,z,w}2 = {x2-y2-z2-w2,2(xy+zw), 2(xz+yw), 2(xw+yz)}
上图是Bristorbrot Set
所用迭代公式:{x,y,z}2 = {x2-y2-z2,y(2x-z),z(2x+y)}
上图所用迭代公式:{x,y,z}2 = {x2-y2-z2,2xy, 2(x-y)z}
作者DavidMakin