【超详细笔记】概率:中心极限定理的直观理解——样本均值为何趋近正态
中心极限定理的直观理解
- 参考教程
- 引例
- 中心极限定理(样本均值的渐近性)
- 掷骰子示例
- 样本与均值
- 软件模拟
- 模拟1-均匀分布
- 模拟2-偏态分布
- 模拟3-自定义分布
参考教程
中心极限定理的直观理解
引例
- 上海平均收入
从中抽样100个人的收入,试图用样本的均值求总体的均值。
因为不可能只有一个样本,所以要再抽几个100人,我们就想知道这么多的样本的样本均值,满足的了什么规则,他们的均值画在横线上会呈现什么分布,研究这是有意义的。

- 机床加工螺丝
螺丝的直径偏差受很多因素的影响,设影响螺丝加工的因素为独立随机变量::
(1)机床 X1X_1X1
(2)刀具 X2X_2X2
(3)材料 X3X_3X3
(4)人 X4X_4X4
…XnX_nXn
一个螺丝总影响 YYY 为各因素之和:
Y=X1+X2+⋯+XnY = X_1 + X_2 + \cdots + X_n Y=X1+X2+⋯+Xn
然后我们想知道一万个螺丝受到的影响是什么分布,也就是想看Xˉ\bar{X}Xˉ符合什么分布
中心极限定理(样本均值的渐近性)
设总体 XXX的期望EX=μEX = \muEX=μ,样本均值Xˉ=X1+X2+⋯+Xnn\bar{X} = \frac{X_1 + X_2 + \cdots + X_n}{n}Xˉ=nX1+X2+⋯+Xn。
当 n→∞n \to \inftyn→∞ 时,样本均值Xˉ\bar{X}Xˉ 渐近服从正态分布,且:
EXˉ=EX=μE\bar{X} = EX = \mu EXˉ=EX=μ
即Xˉ∼渐近N(μ,DXn)\bar{X} \stackrel{\text{渐近}}{\sim} N(\mu, \frac{DX}{n})Xˉ∼渐近N(μ,nDX)(完整形式需结合方差,核心结论为“大样本下均值近似正态,期望等于总体期望” )。
掷骰子示例
设随机变量 XXX 表示掷骰子点数,其分布满足:
X∼{1,P=162,P=163,P=164,P=165,P=166,P=16X \sim \begin{cases} 1, & P = \frac{1}{6} \\ 2, & P = \frac{1}{6} \\ 3, & P = \frac{1}{6} \\ 4, & P = \frac{1}{6} \\ 5, & P = \frac{1}{6} \\ 6, & P = \frac{1}{6} \end{cases} X∼⎩⎨⎧1,2,3,4,5,6,P=61P=61P=61P=61P=61P=61
样本与均值
- 样本一:[3,4,5,…,1,3][3, 4, 5, \dots, 1, 3][3,4,5,…,1,3],均值经计算为 2.72.72.7 ,即 Xˉ1=2.7\bar{X}_1 = 2.7Xˉ1=2.7
- 样本二:[1,1,2,…,3,3][1, 1, 2, \dots, 3, 3][1,1,2,…,3,3],均值经计算为 4.24.24.2 ,即 Xˉ2=4.2\bar{X}_2 = 4.2Xˉ2=4.2
- 样本三:(数据省略 ),均值设为 3.33.33.3 ,即 Xˉ3=3.3\bar{X}_3 = 3.3Xˉ3=3.3

平均值的分布就是正太分布
软件模拟
模拟1-均匀分布

黑屏:分布,现在选择的是均匀分布
32:相当于32面体骰子

N=10:相当于投掷10次

点击Animated模拟一次

一次抽样的平均值

十万次现象:

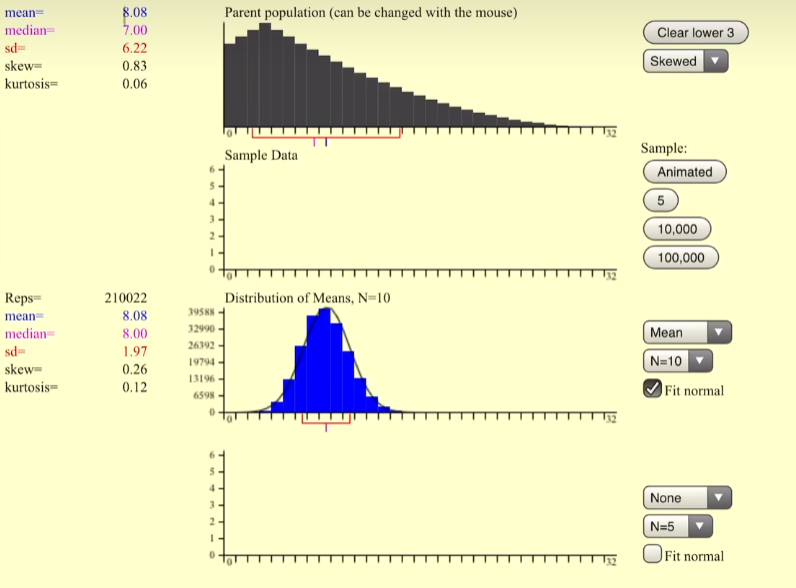
模拟2-偏态分布
现在选了一个这样的分布,期望是8.08


模拟一次抽样

一万次

二十一万次
看到期望也是8.08
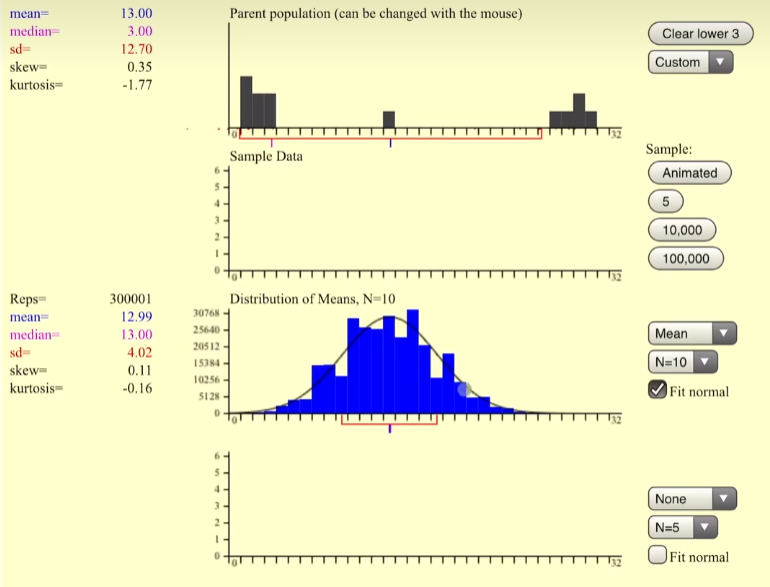
模拟3-自定义分布
随便画个分布,如图,均值13
模拟一次
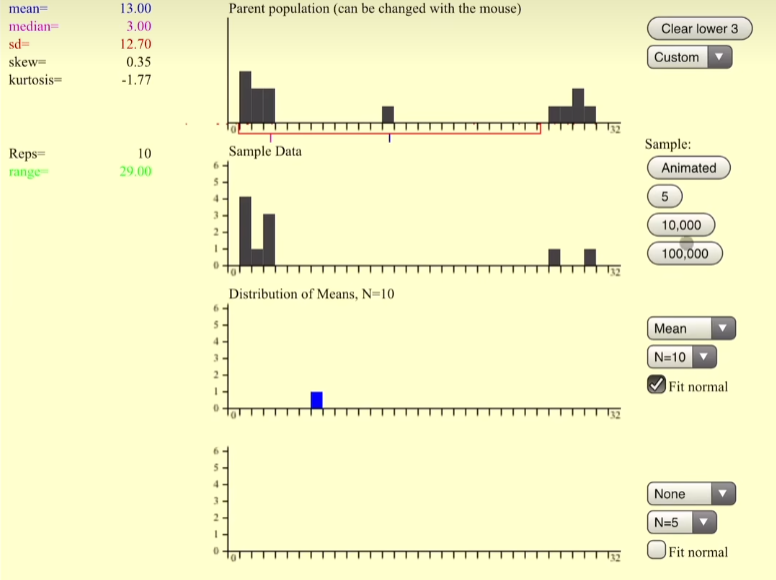
三十万次
可以看到基本上也是一个正太分布,均值12.99约等于13