代码随想录算法训练营第二十天|回溯part02

LeetCode 39 组合总和

题目链接：39. 组合总和 - 力扣（LeetCode）

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。 

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：

输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。
示例 2：

输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3：

输入: candidates = [2], target = 1
输出: []

 本题集合里的元素可以用无数次，那么和组合问题的区别其实就在于startIndex的控制。

本题搜索的过程抽象成树形结构如下：

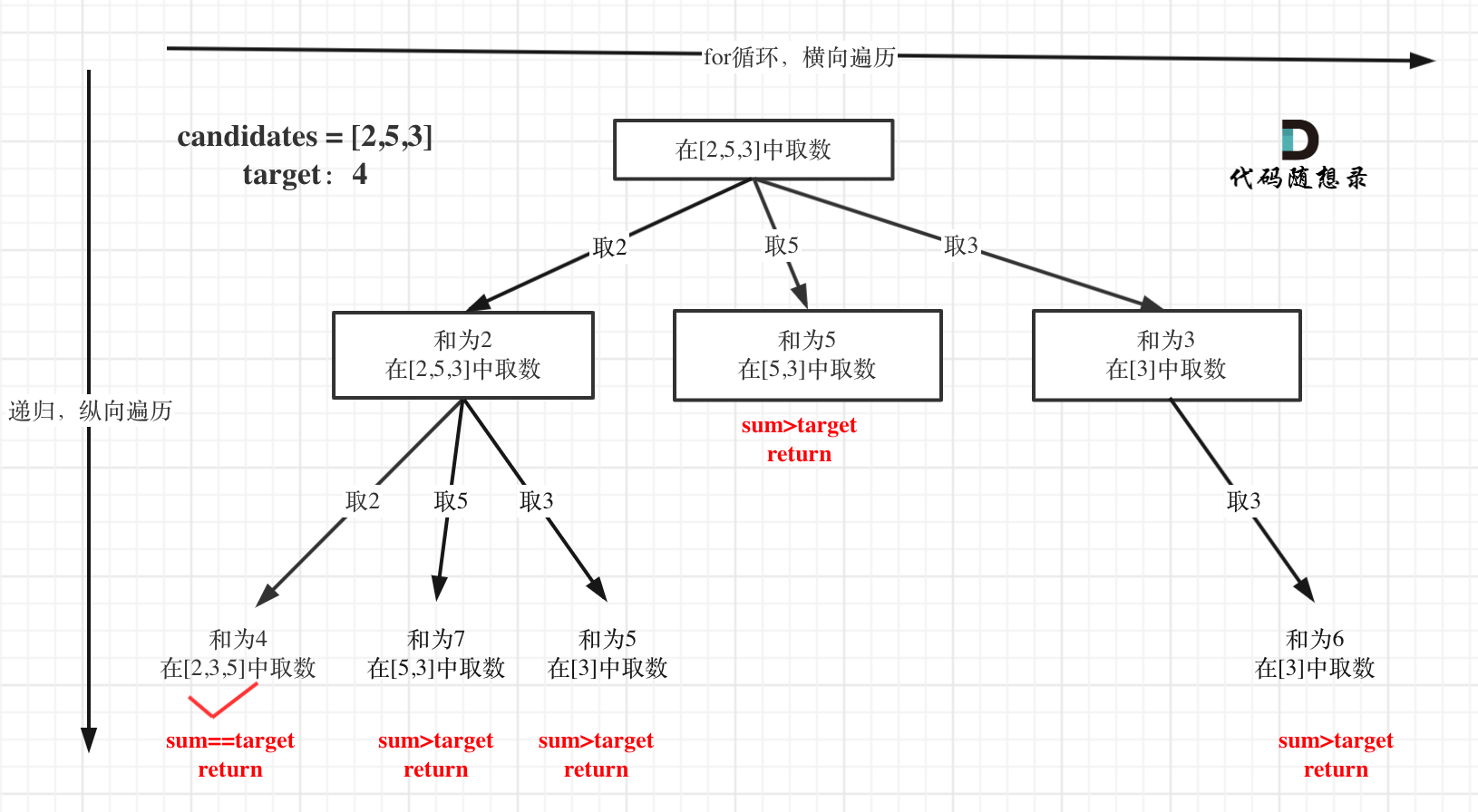
因为本题没有组合数量的要求，所以递归没有层数的限制，只要选取的元素总和超过target，就返回。 

回溯函数定义：

public void backtracking(int[] arr, int target, int sum, int index) 

终止条件：

if (sum > target)return;
if (sum == target) {res.add(new ArrayList<>(list));return;
}

单层递归的逻辑：

for (int i = startIndex; i < arr.length; i++) {list.add(arr[i]);sum += arr[i];backtracking(arr, target, sum, i);sum -= arr[i];list.remove(list.size() - 1);
}

单层for循环依旧是从startIndex开始，但关键是backtracking(arr, target, sum, i);这里不再是i+1，因为本题中元素时可以重复选取的。

所以完整代码如下：

class Solution {List<List<Integer>> res = new ArrayList<List<Integer>>();List<Integer> list = new ArrayList<>();public List<List<Integer>> combinationSum(int[] candidates, int target) {backtracking(candidates, target, 0, 0);return res;}public void backtracking(int[] arr, int target, int sum, int index) {if (sum > target)return;if (sum == target) {res.add(new ArrayList<>(list));return;}for (int i = index; i < arr.length; i++) {list.add(arr[i]);sum += arr[i];backtracking(arr, target, sum, i);sum -= arr[i];list.remove(list.size() - 1);}}
}

剪枝优化

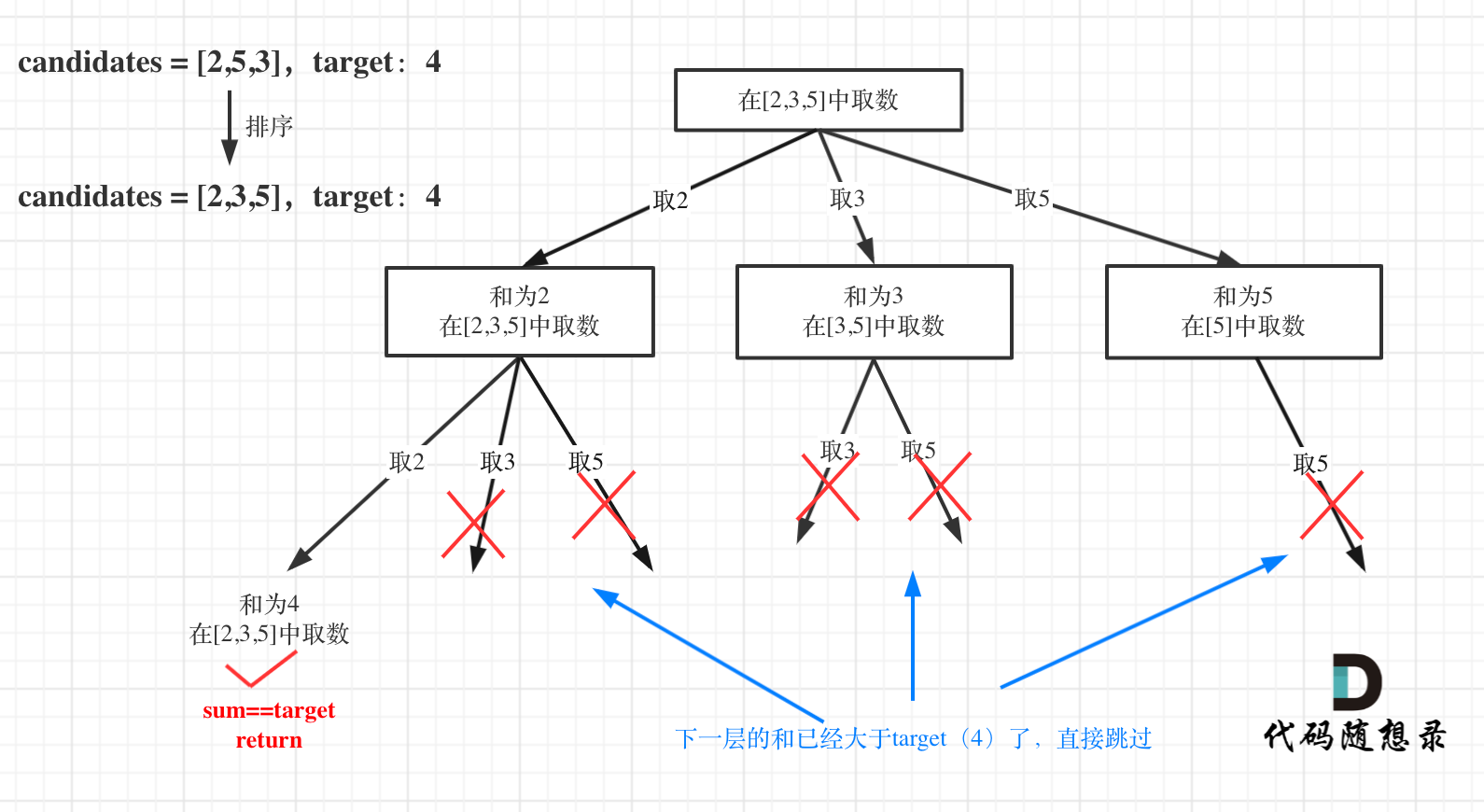
其实上述代码对于sum大于target的情况，依然会进入下一层递归，只是下一层递归结束判断的时候会判断sum>target的话就返回。

其实如果已经知道下一层的sum会大于target，就没有必要进入下一层递归了。

方法就是对总集合排序，如果下一层的sum（也就是本层的sum+candidate[i]）已经大于target，就结束本轮for循环的遍历。

如图所示：

所以优化后的代码：

class Solution {List<List<Integer>> res = new ArrayList<List<Integer>>();List<Integer> list = new ArrayList<>();public List<List<Integer>> combinationSum(int[] candidates, int target) {Arrays.sort(candidates);backtracking(candidates, target, 0, 0);return res;}public void backtracking(int[] arr, int target, int sum, int index) {if (sum > target)return;if (sum == target) {res.add(new ArrayList<>(list));return;}for (int i = index; i < arr.length; i++) {if(sum+arr[i]>target)break;list.add(arr[i]);sum += arr[i];backtracking(arr, target, sum, i);sum -= arr[i];list.remove(list.size() - 1);}}
}

 LeetCode 40 组合总和II

题目链接：40. 组合总和 II - 力扣（LeetCode）

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用 一次 。

注意：解集不能包含重复的组合。 

示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
示例 2:

输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]

 本题涉及到一个问题：去重

因为题目中给我们集合是由重复元素的，那么求出来的组合就有可能重复，但是题目要求不能有重复组合，所以我们要做去重操作。

所谓去重，就是使用过的元素不能重复选取。

这个“使用过”在树形结构上可以是在同一树枝上使用过，也可以是同一树层使用过。根据题目要求，我们要去重的是同一树层上的“使用过”，同一树枝上的都是一个组合中的元素，不用去重。

举个例子：candidates=[1,1,2],target=3

选择过程的树形结构如图所示：

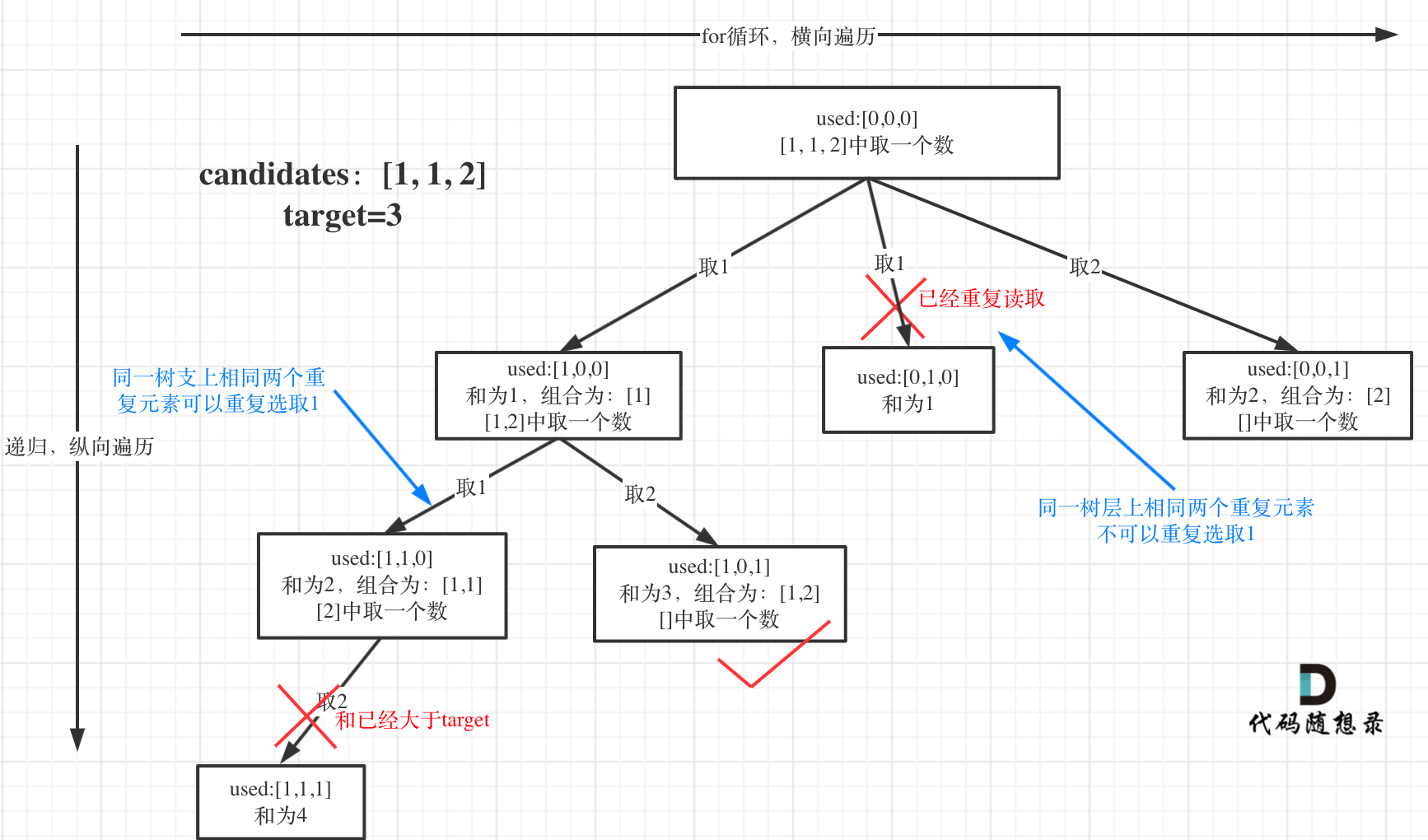
可以看到引入了一个used数组，这个数组就是用来判断同一树层上的元素是否使用过。

当candidates[i] == candidates[i - 1]时，如果used[i-1]==true，说明是在同一树枝上的，可以重复选取；但如果used[i-1]==false，说明是在同一层的，不可以重复选取。

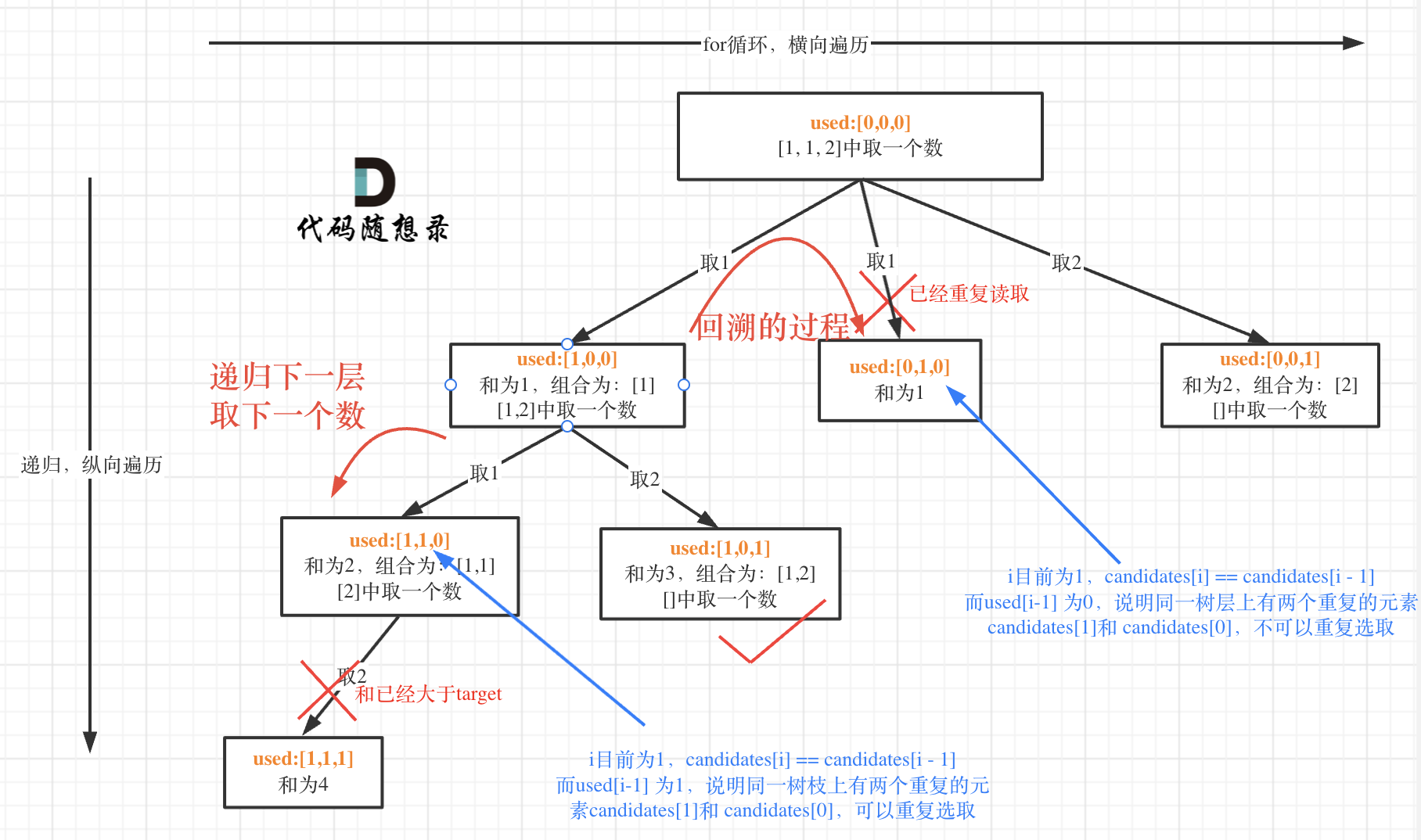
 所以单层的递归逻辑可以是:

public void backtracking(int[] arr,int target,int sum,int index,boolean[] used){if(sum==target){res.add(new ArrayList<>(list));return;}for(int i=index;i<arr.length;i++){if(i>0&&arr[i]==arr[i-1]&&used[i-1]==false)continue;if(sum+arr[i]>target)break;list.add(arr[i]);sum+=arr[i];used[i]=true;backtracking(arr,target,sum,i+1,used);used[i]=false;sum-=arr[i];list.remove(list.size()-1);}}

总代码：

class Solution {List<List<Integer>> res=new ArrayList<List<Integer>>();List<Integer> list=new ArrayList<>();public List<List<Integer>> combinationSum2(int[] candidates, int target) {boolean[] used=new boolean[candidates.length];Arrays.sort(candidates);backtracking(candidates,target,0,0,used);return res;}public void backtracking(int[] arr,int target,int sum,int index,boolean[] used){if(sum==target){res.add(new ArrayList<>(list));return;}for(int i=index;i<arr.length;i++){if(i>0&&arr[i]==arr[i-1]&&used[i-1]==false)continue;if(sum+arr[i]>target)break;list.add(arr[i]);sum+=arr[i];used[i]=true;backtracking(arr,target,sum,i+1,used);used[i]=false;sum-=arr[i];list.remove(list.size()-1);}}
}

或者更简单的直接用index去重，不需要再使用used数组：

public void backtracking(int[] arr,int target,int sum,int index){if(sum==target){res.add(new ArrayList<>(list));return;}for(int i=index;i<arr.length;i++){//跳过同一层中使用过的元素if(i>index&&arr[i]==arr[i-1])continue;if(sum+arr[i]>target)break;list.add(arr[i]);sum+=arr[i];backtracking(arr,target,sum,i+1);sum-=arr[i];list.remove(list.size()-1);}}

LeetCode 131 分割字符串

题目链接：131. 分割回文串 - 力扣（LeetCode）

给你一个字符串 s，请你将 s 分割成一些 子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。

示例 1：

输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]
示例 2：

输入：s = "a"
输出：[["a"]]

 本题抽象为树形结构：

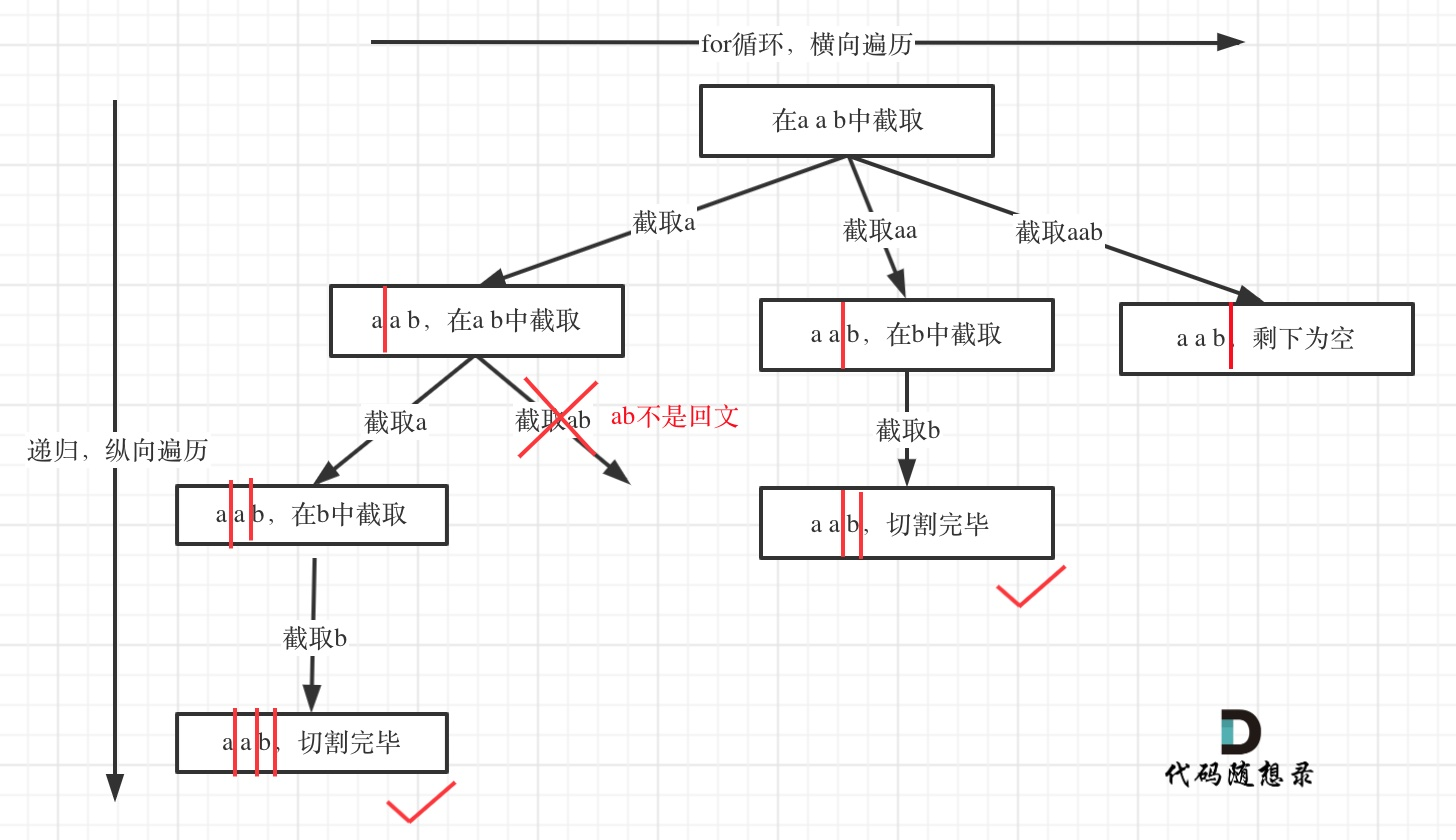
 怎么判断回文串？给定两个指针，一个指针从前向后，一个从后向前，如果这两个指针指向的元素始终是相等的，就是回文串。

代码如下：

public boolean isReverse(String s, int start, int end) {while (start < end) {if (s.charAt(start) != s.charAt(end))return false;start++;end--;}return true;}

再来看回溯函数怎么写。

函数的参数就是字符串s和startIndex；终止条件就是startIndex的大小大于s的大小。

单层搜索的逻辑：

在for (int i = startIndex; i < s.length(); i++)循环中，起始位置为startIndex，那么[startIndex,i]就是要截取的子串。首先判断这个子串是不是回文串，如果是，就加入list中。

代码如下：

public void backtracking(String s, int startIndex) {if (startIndex >= s.length()) {res.add(new ArrayList<>(list));return;}for (int i = startIndex; i < s.length(); i++) {String s1 = s.substring(startIndex, i + 1);if (isReverse(s, startIndex, i)) {list.add(s1);backtracking(s, i + 1);list.remove(list.size() - 1);}}}