【初识数据结构】CS61B中的基本图算法:DFS, BFS, Dijkstra, A* 算法及其来历用法
CS61B中关于图中的路径问题介绍了很多种算法,这些算法之间根据不同的情况做出了相对应的调整,虽然差别不大,但是做个小整理
这里针对寻找路径问题,分别整理了DFS,BFS,Dijkstra 算法,A* 算法
Princeton Graph API
这里是 Princeton Algorithm textbook 中给出的图接口,其余方法需要自己添加进行实现
public class Graph{public Graph(int V);public void addEdge(int v, int w);Iterable<Integer> adj(int v);int V();int E();
}
这里要注意几个点:
- 顶点的数量提前由构造函数确定,不可后期更改
- 不支持在结点或者边上设置权重
- 没有针对某个特殊结点得到其边数(度)的方法
一位观世音菩萨——Paths.java
在一般的图算法设计模式中,我们会将类型进行解耦
比如我们会这样做:
- 创造一个图对象
- 将这个图传递到一个图处理方法或者客户类中
- 然后询问这个客户类关于这个图的一些信息
就像有一位贤知的观世音菩萨一样:
public class Paths{public Paths(Graph G,int s);boolean hasPathTo(int v);Iterable<Integer> pathTo(int v);
}
这个Paths类就记录了我们传入的Graph中的所有路径信息
遍历所有路径(不考虑边权重以及结点代价)
1.深度优先算法(DFS)
两个辅助数组:
boolean[] markedint[] edgeTo
算法流程
dfs(v):
- 标记 v
- 对每一个相邻的结点 w
- 设置 edgeTo[w] = v
- dfs(w)
算法特征
对于DFS算法有一个特征是:
调用DFS算法的顺序是先序遍历的,而返回DFS算法的顺序是后续遍历的
算法实现:
public class DepthFirstPaths{private boolean[] marked;private int[] edgeTo;private int s;...public Iterable<Integer> pathTo(int v){if(!hasPathTo(v)){return null;}List<Integer> path = new ArrayList<>;for(int x = v;x != s; x = edgeTo[x]){path.add(x);}Collection.reverse(path);return path;}public boolean hasPathTo(int v){return marked[v];}
}
2.宽度优先算法(BFS)
一个辅助队列
初始化一个队列,将一个起点放入队列中,我们把这个队列称作为fringe
算法流程
一直重复以下操作直到队列为空:
- 将队列第一个结点移出
- 对于该结点的每个未标记的相邻结点n:
- 标记 n
- 将 edgeTo[n] 设置为 v(或者distTo[n] = distTo[v] + 1)
- 将 n 加入该队列
算法实现
public class BreadthFirstPaths{private void bfs(Graph G,int s){Queue<Integer> fringe = new Queue<Integer>();fringe.enqueue(s);marked[s] = true;while(!fringe.isEmpty()){int v = fringe.dequeue();for(int w: G.adj(v)){fringe.enqueue(w);marked[w] = true;edgeTo[w] = v;}}}
}
上面这两种算法的缺点
DFS 对于细长的图表现得很坏
- 会让函数调用栈变得特别长
BFS 对于茂盛的图表现得很坏
- fringe 会变得非常长
并且我们需要 V 的内存来追踪distTo和edgeTo数组
考虑权重的遍历
如果图中每条路径都有权重,比如谷歌地图中我们想找到距离目的地最近的路线呢
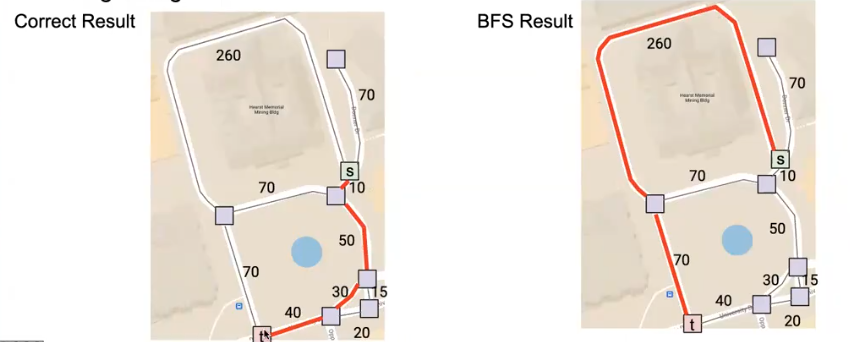
我们会发现只考虑边数是不够的,这样会得出错误的答案,每条边具有对应的长度,也就是权重,这时我们应该采用什么算法呢
最短路径树
探究这样一个问题:给定一个起点 s 找到对于其他所有顶点的最短路径
这样我们画出来的这个路径称作为最短路径树(SPT)
迪杰斯特拉算法(Dijkstra’s Algorithm)
三种坏算法
让我们先看三种坏算法,来引入Dijkstra
1.BFS
不考虑权重直接将没有见过的结点加入树中
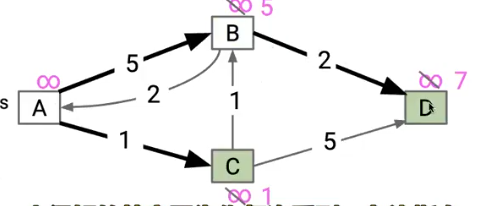
显然这是一个坏算法,构造出了一个错误的SPT,这是因为我们从A开始,直接把BC都加入了树中,而这条A->B的路径并不是最好的路径,这个只考虑node问题,没有见过的node直接加入
2.虚拟结点
我们把所有路径上的权重看作为一个个虚拟结点:
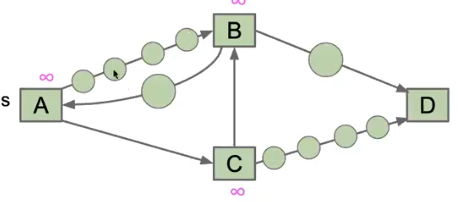
该算法按照距离起点的远近来将对应的结点加入树,考虑distance的问题,也就是最好优先,这里已经开始触及最核心的部分了
但是我们为什么也不用这个算法呢:
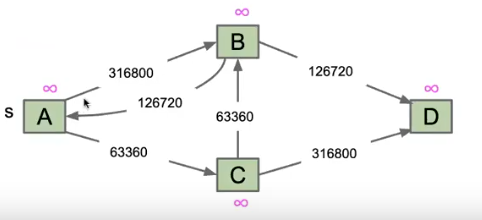
我们不会创造这么多个虚拟结点
3.best first
当fringe不为空时:
- 将最近的结点移出,然后进行标记
- 对于每个出边 v->w : 如果 w 不再 SPT中,那么加入这条边,然后将 w 加入fringe
这个算法有什么问题呢:
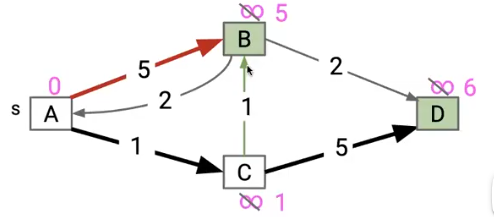
我们会发现,他会先把 A->B 加入SPT中,但后续我们考虑 C->B时就会直接跳过他
这个算法中给出的第一个解法太强势了,即使后面的解法更好,他也不做考虑,像一个顽固的老头!
Dijkstra
通过考虑上面三种坏算法,我们发现需要做以下两种修复:
- 根据距离来考虑结点
- 对每个边 v->w :如果这条边给出了更好的到 w 的距离,那我们就把这条边加入,然后在 fringe 中更新 w
我们会借助一个优先队列PQ,将所有的结点加入PQ,根据到起点的距离排序,然后重复:
- 将最近的结点 v 从 PQ 移出,然后 “relax” 从 v 指出的所有边
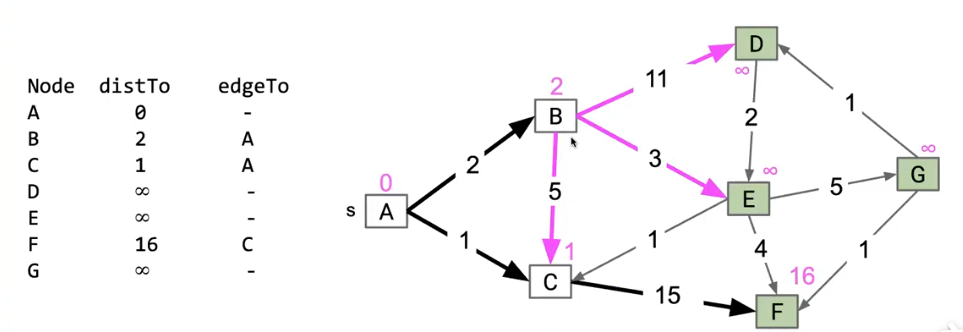
在这个图中我们的流程是:
- 所有结点的dist设置为无穷大
- 从A开始
- 走A->C,distTo[C] = 1
- 走A->B, distTo[B] = 2
- A走完,然后A被标记,即已访问A
- 考虑BC中最近的
- 访问C
- 走 C->F, distTo[F] = distTo[C] + 15 = 16
- C被标记
- 考虑 BF 中最近的
- 访问B
- 走B->C,发现 distTo[B] + 5 > discTo[C],不是更优路径,不考虑
- 走B->E, distTo[E] = distTo[B] + 3 = 5
- 走B->D, distTo[D] = distTo[B] + 11 = 13
- B被标记
- 考虑DEF中最近的
- …
总结来说就是
- 取出当前PQ中最近的结点,然后将其相邻所有更好的方案结点加入PQ中,然后重复
如果我们发现了更好的方案,我们只需要更新edgeTo数组即可(改变路径),同时更新 distTo 数组来记录更好的距离
弊端
如果使用了负权重,Dijkstra 算法则会失效
伪代码
- PQ.add(source, 0)
- For other vertices, PQ.add(v, infinity)
- While PQ is not empty:
- p = PQ.removeSmallest()
- Relax all edges from p
- Relaxing an edge p->q with weight w:
- If distTo[p] + w < distTo[q]
- distTo[q] = distTo[p] + w
- edgeTo[q] = p
- PQ.changePriority(q, distTo[q])
- If distTo[p] + w < distTo[q]
不变量
- edgeTo[v] 是已知的v的最好路径前缀
- distTo[v] 是已知的最好的 v 的路径长度
- PQ按顺序容纳了所有未访问过的结点
重要性质
- 总是从起点开始按距离访问结点
- relaxation在每次边指向已经访问过的结点的时候都会失败
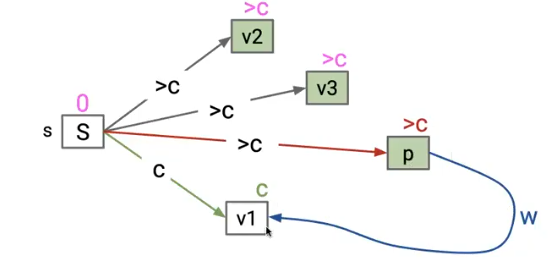
看上面这个图就很好理解了
不想要进行遍历——启发性算法
上面的算法我们都尝试对所有的结点进行遍历,从而找出最短路径,但是看下面的情况:
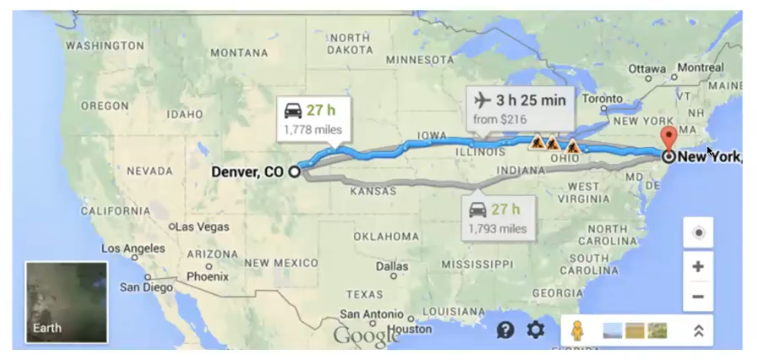
我们只想从Denver,CO 到 New York,大致方向上来说我们需要向东行驶,如果我们使用Dijkstra算法,我们同样会遍历所有结点,但是显然向西方行驶是荒谬的!
所以我们采取在每个节点上加上代价的方式,来规避我们不想去的方向,由此我们得到了 A* 算法(A star)
A* Algorithm
我们看下面这个 A* 算法实例:
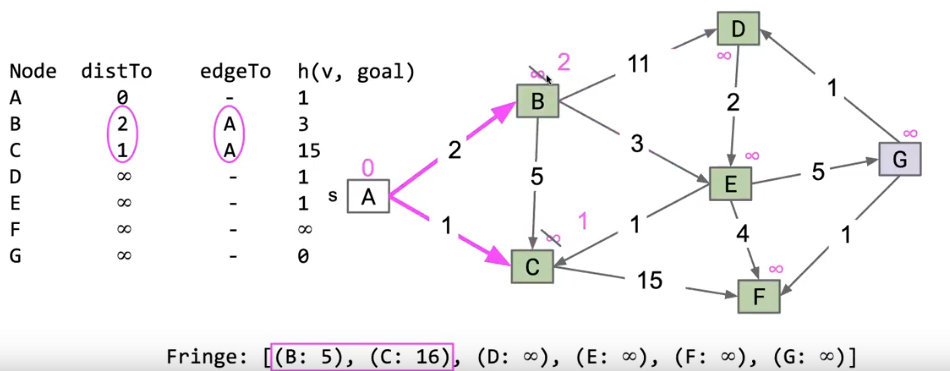
在算法的流程上和Dijkstra 算法大致相同,但是在我们进行算法之前,我们会得到一个代价数组,记录了每个结点的代价,而与之对应的,我们的Fringe不再以距离作为排序标准,而是用距离加上当前代价作为标准
注意
Fringe中的代价只是路径加上当前结点的代价,路径中经过的结点代价不算,也就是说,A* 算法的 distTo 数组仍然保持不变,只是加上了当前结点的代价作为Fringe数组的排序标准
这样通过一个代价数组得到启发,从而有选择性的往某些结点或方向探索的算法,被称为启发性算法
