算法题（175）：小明的游戏

审题：

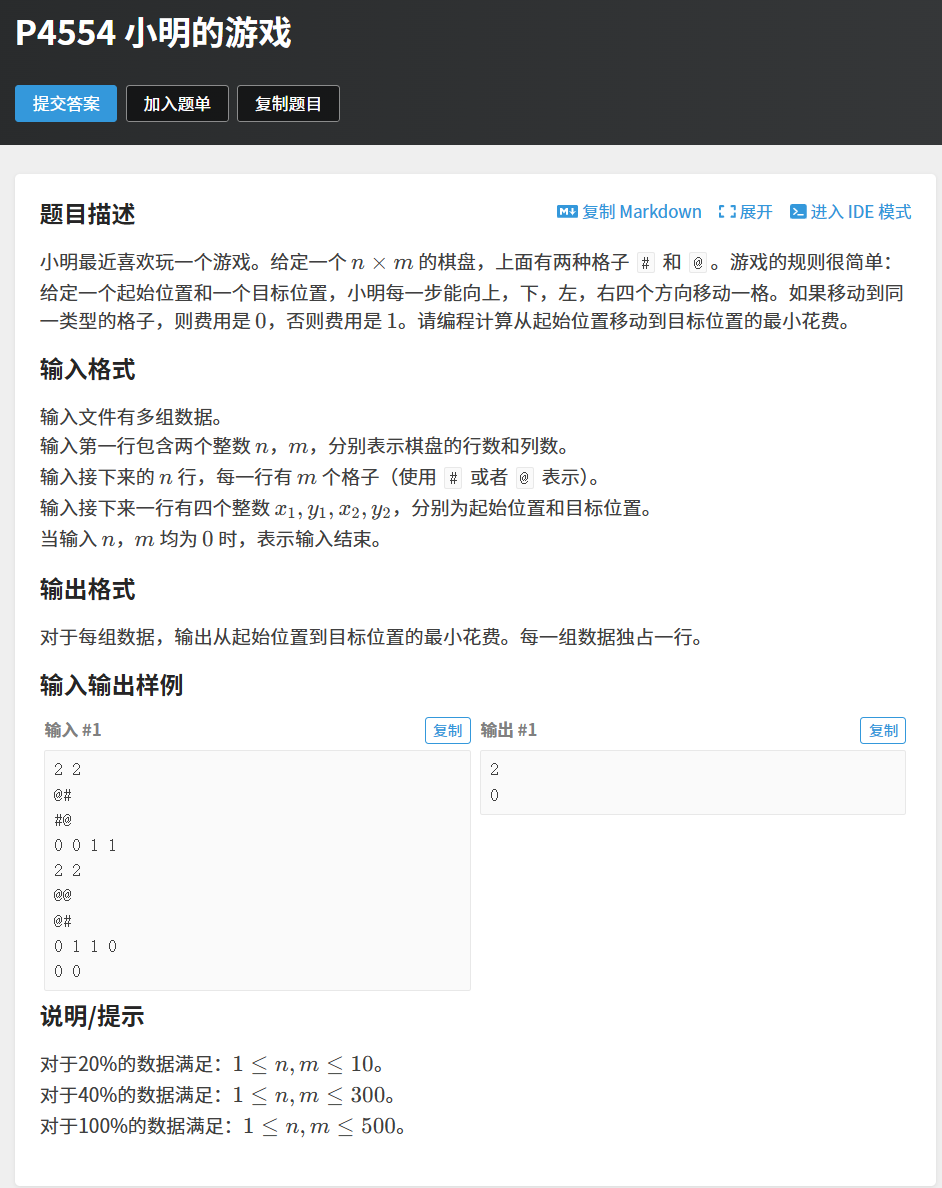
本题需要我们找到从起点到终点所需的最短距离并输出（多组输入输出）

思路：
方法一：01BFS

由于本题的目的是找最短路径，所以我们可以采用bfs来进行搜索，而路径权值并非都为1，而是有0有1.故我们采用01BFS

补充：

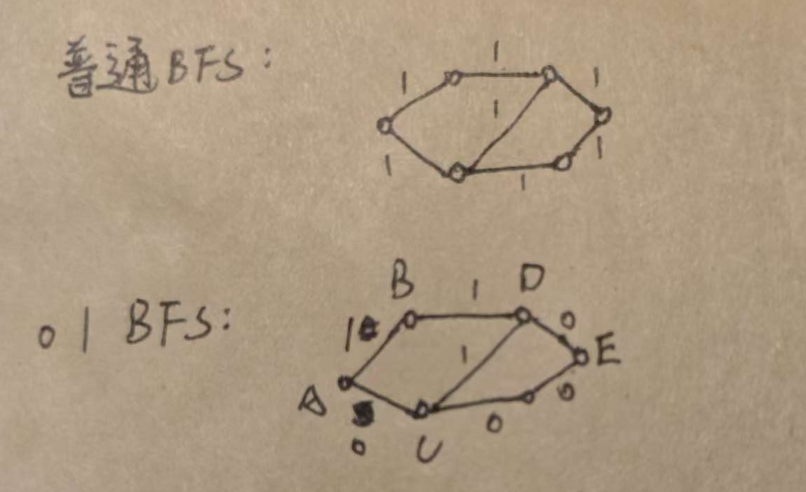
普通BFS：路径权值都为1，直接按轮次搜索即可

能成功的本质：权值为1，dis数组的值都是非递减的，所以每一个位置第一次到达的距离一定是到他的最短距离

01BFS：路径权值为1或0，需要对数据顺序进行排序，还要进行松弛操作将最优距离计入

解题：

#include<iostream>
#include<deque>
#include<cstring>
using namespace std;
typedef pair<int, int> PII;
const int N = 510;
int n, m, x1, x2, y1, y2;
char a[N][N];//字符数组
int dis[N][N];//距离数组
int dx[] = { 1,-1,0,0 };
int dy[] = { 0,0,1,-1 };
void bfs()//01bfs
{if (x1 == x2 && y1 == y2){dis[x2][y2] = 0;return;}//痕迹清除deque<PII> q;memset(dis, -1, sizeof(dis));q.push_front({ x1,y1 });dis[x1][y1] = 0;//循环搜索路径while (q.size()){PII t = q.front(); q.pop_front();int x0 = t.first; int y0 = t.second;if (x0 == x2 && y0 == y2){return;}for (int i = 0; i < 4; i++){int x = x0 + dx[i]; int y = y0 + dy[i];if (x >= 0 && x < n && y >= 0 && y < m){char cur = a[x0][y0], next = a[x][y];int w = (cur == next ? 0 : 1);if (dis[x][y] == -1)//第一次遇到{dis[x][y] = dis[x0][y0] + w;if (w == 0){q.push_front({ x,y });}else{q.push_back({ x,y });}}else if (dis[x0][y0] + w < dis[x][y])//遇到更优情况{dis[x][y] = dis[x0][y0] + w;}}}}
}
int main()
{//数据录入while (cin >> n >> m, n && m){for (int i = 0; i < n; i++){for (int j = 0; j < m; j++){cin >> a[i][j];}}cin >> x1 >> y1 >> x2 >> y2;bfs();cout << dis[x2][y2] << endl;}return 0;	
}

注意：

bfs总体逻辑：先清除痕迹，然后使用双端队列将起点坐标录入，进入bfs搜索。

在确保坐标合法的前提下，判断该坐标是否是第一次遇到，或者该坐标是否可以用更短的距离到达。

1.数据录入的时候使用了逗号表达式，其含义是在n与m不全为0的情况下进行循环数据录入

2.第一次遇到时，若该路径的权值为0，则需要将该坐标的点头插进入双端队列，因为他属于当前轮次搜索的点，否则就尾插即可

3.遇到更优情况：更新dis为最优情况

P4554 小明的游戏 - 洛谷