【专题一】双指针

本博客梳理双指针算法
常见的双指针：对撞指针、快慢指针
1.对撞指针：一般用于顺序结构中
2.快慢指针：用两个移动速度不同的指针在数组或者链表等序列结构上移动，对于处理环形链表或数组非常有用，其实对于出现循环往复情况的问题，都可以考虑使用快慢指针
3.针对存在单调性的场景，双指针可以用来大幅度优化暴力枚举

1. 移动零

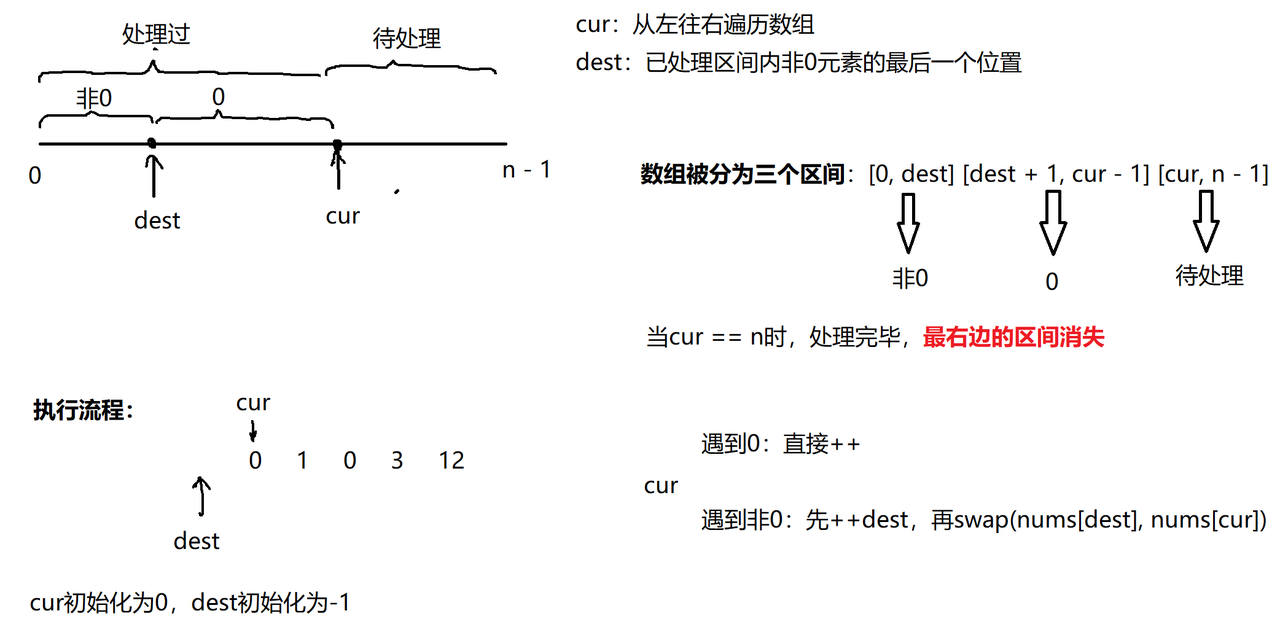
class Solution {
public:void moveZeroes(vector<int>& nums) {if(nums.size() == 1)return;int cur = 0;int dest = -1;while(cur < nums.size()){if(nums[cur] == 0)++cur;else{++dest;swap(nums[dest], nums[cur]);++cur;}}}
};

2. 复写0

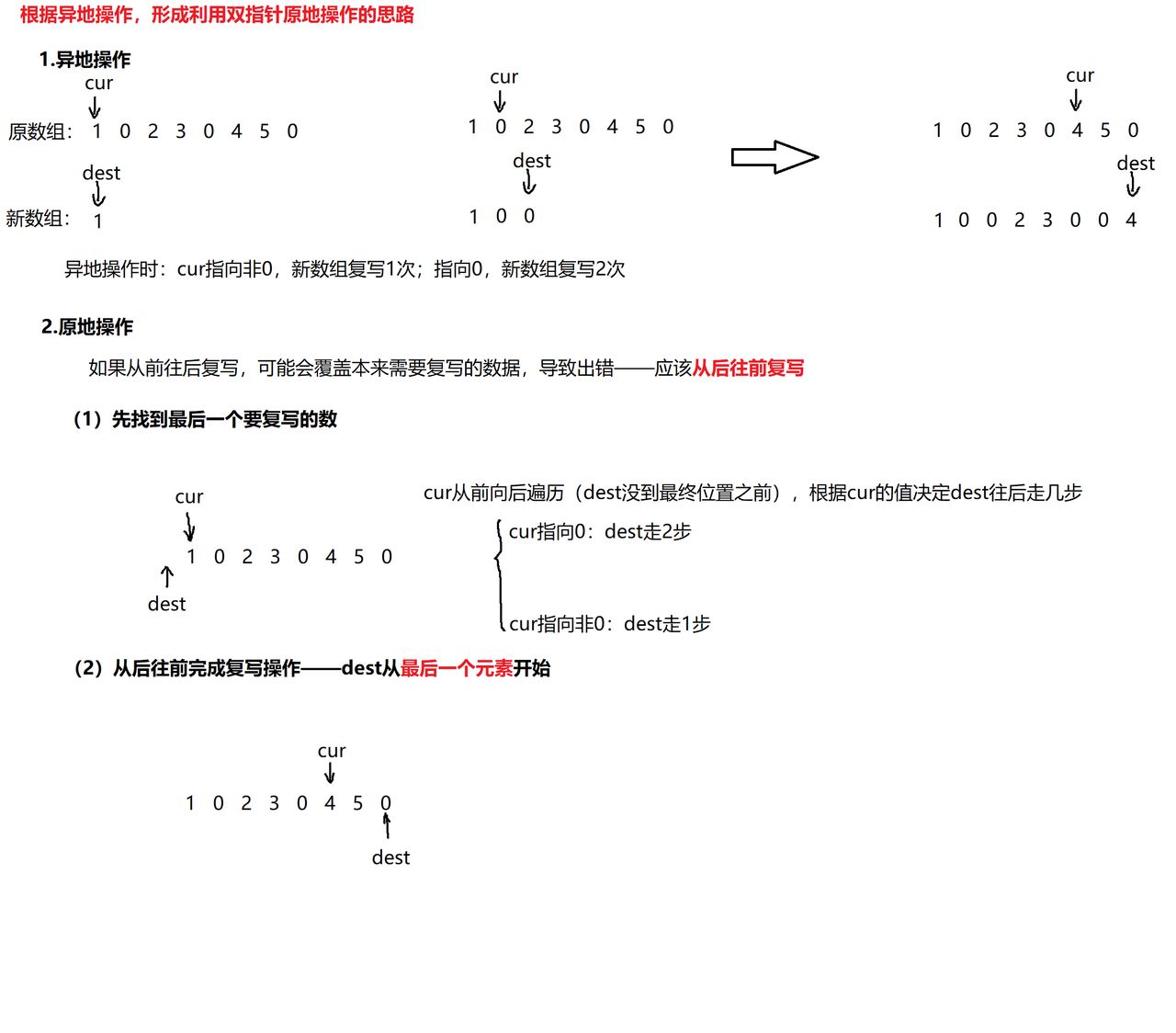
class Solution {
public:void duplicateZeros(vector<int>& arr) {//1.首先找到最后一个要复写的数，再后面的都不用管了int cur = 0;int dest = -1;int n = arr.size();//解决arr.size()返回size_t带来的麻烦while(cur < n){if(arr[cur] == 0)dest += 2;else++dest;if(dest >= n - 1)break;++cur;}//此时cur已经指向了最后一个需要复写的数//处理一下边界情况：如果dest == n，则说明cur指向了0，复写产生了越界if(dest == n){//此时理论上n - 1和n位置都要复写0，但n位置越界，要特殊处理一下--dest;arr[dest] = 0;--dest;--cur;}//2.从后向前完成复写操作while(cur >= 0){if(arr[cur] == 0){arr[dest--] = 0;arr[dest--] = 0;}elsearr[dest--] = arr[cur];--cur;}}
};

3. 快乐数

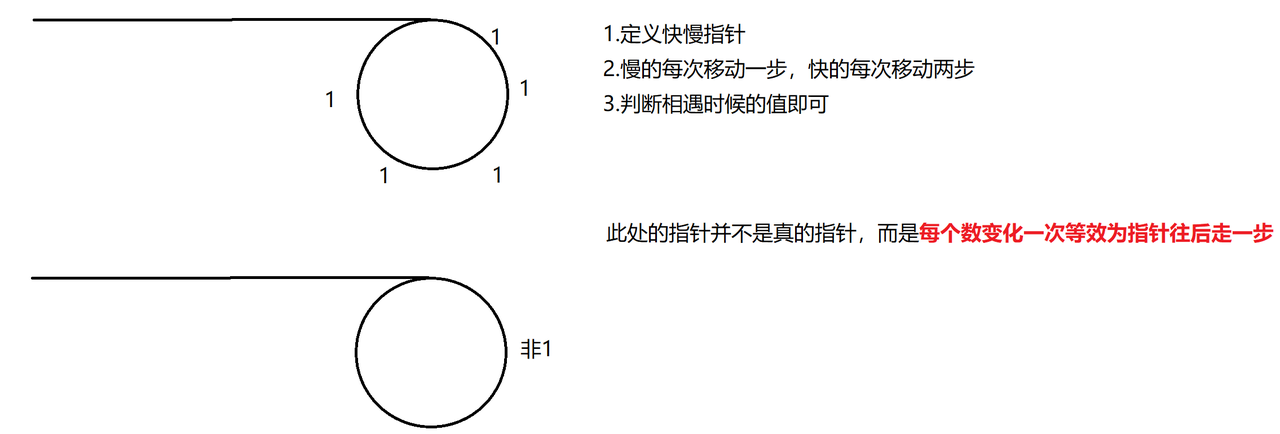
3.1 快慢指针的特性

在一个圆圈中，快指针总会追上慢指针。针对本题，如果快慢指针相遇的位置值为1，则说明是快乐数；相遇的位置值不为1，则说明不是快乐数

3.2 证明一下：为什么一定会进入循环？

int的最大值为2147483647，直接找一个数9999999999，根据题意变化一次后最大值为810，之后这个数无论怎么操作，一定落在[1,810]之间。假设最坏情况是变化810次的值都不同，没产生循环，那么第811次的值必产生循环

3.3 本题解法

class Solution {
public:int squared_sum(int n)//获取n的每一位，计算平方和{int sum = 0;while(n != 0){int ones = n % 10;sum = sum + ones*ones;n = n / 10;}return sum;}bool isHappy(int n) {//转化为判断链表是否带环//如果是快乐数，经历若干次变化之后一定会进入重复的一个环里面int slow = n;int fast = squared_sum(n);while(slow != fast){slow = squared_sum(slow);fast = squared_sum(squared_sum(fast));if(slow == fast)//最终必定成环，快指针一定追上慢指针break;}if(slow == 1 && fast == 1)return true;elsereturn false;}
};

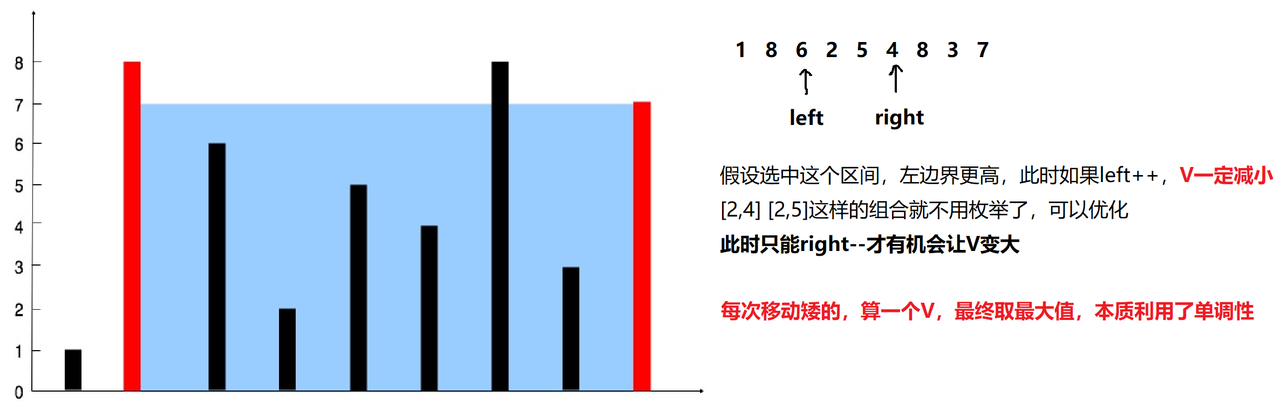
4. 盛水最多的容器

4.1 解法一：暴力枚举

两层for循环，枚举左右边界，找最大值（会超时）

4.2 解法二：对撞指针

4.2.1 对暴力求解的优化

暴力枚举无脑把所有情况都列出来了，但有些情况是冗余的，没必要枚举

4.2.2 本题解法

class Solution {
public:int maxArea(vector<int>& height) {int left = 0;int right = height.size() - 1;int ret = 0;while(left < right){int h = min(height[left], height[right]);int width = right - left;int V = h * width;ret = max(ret, V);if(height[left] <= height[right])left++;elseright--;}return ret;}
};

5. 有效三角形的个数

5.1 解法一：暴力枚举

三层for循环枚举所有的三元组，然后三次判断两边之和大于第三边。缺点：枚举冗余，大量低效枚举

5.2 解法二：排序+双指针

5.2.1 对暴力求解的优化

1. 如果能构成三角形，只需两个小的边加起来大于第三边即可
2. 因此可以先将原数组排序，从小到大枚举三元组

5.2.2 本题解法

既然对数组进行了排序，那就有了单调性，可以考虑双指针

class Solution {
public:int triangleNumber(vector<int>& nums) {//首先：如果a ≤ b ≤ c，那么只需a + b < c，必能构成三角形//因此：如果整个数组有序，统计起来肯定更方便//所以：利用单调性，配合双指针会优化暴力解法sort(nums.begin(), nums.end());int max = nums.size() - 1;int ret = 0;while(max >= 0){int c = nums[max];int left = 0, right = max - 1;while(left <= right){if(nums[left] + nums[right] > c)//说明可以构成三角形{//符合条件的三元组个数：right - leftret += right - left;right--;}elseleft++;//无符合条件的三元组，只有left++才有希望出现}--max;}return ret;}
};

6. 两数之和

6.1 解法一：暴力求解

两层for循环列出所有数字的组合，判断是否等于目标值（超时）

6.2 解法二：单调性+双指针

优化暴力枚举：题目中已经指出数组有序，因此可以用双指针优化

class Solution {
public:vector<int> twoSum(vector<int>& price, int target) {int left = 0, right = price.size() - 1;while(left < right){int sum = price[left] + price[right];if(sum > target)right--;else if(sum < target)left++;elsereturn {price[left], price[right]};}return {-1, -1};}
};

7. 三数之和

7.1 解法一：排序+暴力枚举+利用set去重

7.2 解法二：单调性+双指针

class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>> vv;sort(nums.begin(), nums.end());//固定一个数a，后面用双指针，找nums[left] + nums[right] = -aint i = 0;while(i < nums.size()){int left = i + 1;int right = nums.size() - 1;int a = nums[i];//最左边固定的那个数vector<int> v;while(left < right){if(nums[left] + nums[right] == -a){v = {a, nums[left], nums[right]};vv.push_back(v);//缩小[left, right]继续找//先处理left++left;while(left < right && nums[left] == nums[left - 1])//跳过重复元素++left;//再处理right--right;while(left < right && nums[right] == nums[right + 1])//跳过重复元素--right;}else if(nums[left] + nums[right] > -a)--right;else++left;}++i;while(i < left && nums[i] == nums[i - 1])i++;}return vv;}
};