当前位置：首页 > news >正文

7.19 pq | 并查集模板❗|栈循环|数组转搜索树

news 2025/7/19 18:18:11

并查集2.0

新增num-of-sets，可以通过==1，判连通

class UnionFind {
public:
UnionFind(int n) {
p = vector<int>(n + 1);
size = vector<int>(n + 1, 1);
iota(p.begin() + 1, p.end(), 1);
num_of_sets = n;
}

int find(int x) {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
}

bool connected(int a, int b) {
return find(a) == find(b);
}

void merge(int x, int y) {
int px = find(x), py = find(y);
if (px != py) {
if (size[px] > size[py]) {
p[py] = px;
size[px] += size[py];
} else {
p[px] = py;
size[py] += size[px];
}
num_of_sets--;
}
}

int num_of_sets;

private:
vector<int> p, size;
};

lc1579.贪心+并查集

先处理alice再处理bob

class Solution {
public:
int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {
int res = 0;
UnionFind uf_alice(n);
UnionFind uf_bob(n);

// 先处理类型3的边
for (auto& edge : edges) {
int _type = edge[0], n1 = edge[1], n2 = edge[2];
if (_type == 3) {
if (!uf_alice.connected(n1, n2))

{
uf_alice.merge(n1, n2);
uf_bob.merge(n1, n2);
}

else {
res++;
}
}
}

// 处理类型1和类型2的边
for (auto& edge : edges)

{
int _type = edge[0], n1 = edge[1], n2 = edge[2];
if (_type == 1) {
if (!uf_alice.connected(n1, n2)) {
uf_alice.merge(n1, n2);
}

else {
res++;
}
}

else if (_type == 2) {
if (!uf_bob.connected(n1, n2))

{
uf_bob.merge(n1, n2);
}

else {
res++;
}
}
}

// 检查是否都连通
if (uf_alice.num_of_sets != 1 || uf_bob.num_of_sets != 1) {
return -1;
}
return res;
}
};

lc665.改值策略

class Solution {
public:
bool checkPossibility(vector<int>& nums)

{
int check = 0;
int n = nums.size();
if (n < 2) return true;

for (int i = 0; i < n - 1; i++) {
if (nums[i] > nums[i + 1])

{
check++;
if (check > 1) return false;
if (i > 0 && nums[i + 1] < nums[i - 1]) {
nums[i + 1] = nums[i];
}

else {
nums[i] = nums[i + 1];
}
}
}
return true;
}
};

lc513.栈循环

for (int i = 0; i < 2 * n; i++)

{

int current = nums[i % n];

//栈逻辑处理

if (i < n)

{
st.push(i);
}

} 循环栈即模拟i＜2*n，跑两遍

错误写法

class Solution {
public:
vector<int> nextGreaterElements(vector<int>& nums)
{
stack<int> st;
int n = nums.size(), mx = INT_MIN;
vector<int> ret(n, -1);

for (int i = 0; i < n; i++) {
mx = max(mx, nums[i]);
while (!st.empty() && nums[i] > nums[st.top()]) {
int t = st.top();
st.pop();
ret[t] = nums[i];
}
st.push(i);
}

while (!st.empty()) {
int t = st.top();
st.pop();
if (nums[t] != mx) {
ret[t] = mx;
}
}

return ret;
}
};

正确写法

class Solution {
public:
vector<int> nextGreaterElements(vector<int>& nums)
{
stack<int> st;
int n = nums.size();
vector<int> ret(n, -1);

for (int i = 0; i < 2 * n; i++) {
int current = nums[i % n];

while (!st.empty() && current > nums[st.top()]) {
int topIdx = st.top();
st.pop();
ret[topIdx] = current;
}
if (i < n) {
st.push(i);
}
}
return ret;
}
};

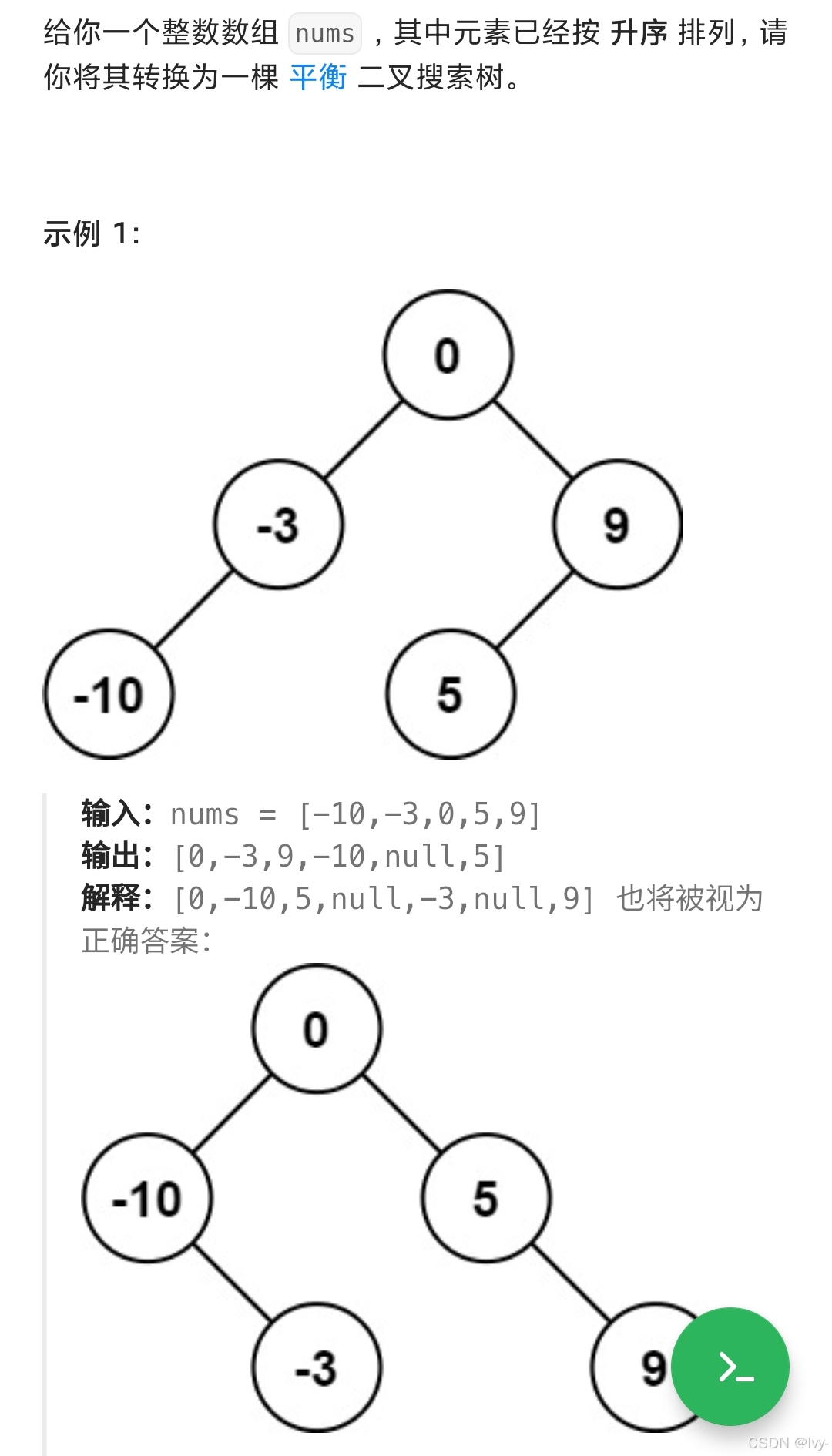
lc168.数组转搜索树
l> r null

mid
root = new
-> l
-> r
return root

class Solution {
vector<int> nums;
int n=0;

public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
n=nums.size();
this->nums=nums;
return dfs(0,n-1);
}

TreeNode* dfs(int l,int r)
{
if(l>r) return nullptr;

int mid=l+(r-l)/2;

TreeNode* root=new TreeNode(nums[mid]);
root->left=dfs(0,mid-1);
root->right=dfs(mid+1,n-1);
return root;
}
};

并查集

class UnionFind

{
public:
UnionFind(int n)

{
p = vector<int>(n);
size = vector<int>(n, 1);
iota(p.begin(), p.end(), 0);
}

bool unite(int a, int b)

{
int pa = find(a), pb = find(b);
if (pa == pb) {
return false;
}
if (size[pa] > size[pb]) {
p[pb] = pa;
size[pa] += size[pb];
} else {
p[pa] = pb;
size[pb] += size[pa];
}
return true;
}

int find(int x) {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
}

bool connected(int a, int b)

{
return find(a) == find(b);
}

private:
vector<int> p, size;
};

lc1631.最小绝对差路径

class Solution {
public:
int minimumEffortPath(vector<vector<int>>& heights) {
int m = heights.size(), n = heights[0].size();
vector<array<int, 3>> edges;
int dirs[3] = {0, 1, 0};

for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
for (int k = 0; k < 2; ++k) {
int x = i + dirs[k], y = j + dirs[k + 1];
if (x >= 0 && x < m && y >= 0 && y < n) {
edges.push_back({abs(heights[i][j] - heights[x][y]), i * n + j, x * n + y});
}
}
}
}
sort(edges.begin(), edges.end());

UnionFind uf(m * n);
for (auto& [h, a, b] : edges)

{
uf.unite(a, b);
if (uf.connected(0, m * n - 1))

{
return h;
}
}
return 0;
}
};

用「并查集」找「最小体力路径」：

1. 把地图变成一堆边

把每个格子看作一个点，计算相邻格子（右、下方向）的高度差，这些高度差就是「移动需要的体力」，记录成“边”（格式：体力值，起点，终点）。

2. 按体力从小到大排序边

先处理体力小的边，这样能优先用省力的方式连接格子。

3. 用并查集“拼”路径

用并查集把边对应的格子连起来，每连一条边就检查：左上角的格子（起点）和右下角的格子（终点）是否连通了。

一旦连通，当前用的这条边的体力值，就是答案——因为我们是从小到大处理的，这时候的体力肯定是最小的。

简单说就是：从小力气的路开始修，哪一刻起点和终点通了，这一刻用的力气就是最小的。