第16章 基于AB实验的增长实践——验证想法:AB实验实践
一、AB实验全流程框架
实验分为5个核心环节:
实验假设 → 实验设计 →实验运行 → 实验分析 → 实验决策
二、各环节核心要点详解
1. 实验假设
原则:目标性、可归因、可复用(前两者必选)
(1)目标性:明确量化目标(例:留存率提升α%),避免事后归因。
案例:红包策略实验需提前声明目标:"通过签到领现金提升DAU β%",而非实验后找上涨指标。
实验目标——明确要提升的核心指标及预期幅度。
- ❌ 模糊目标:“提升用户活跃度”
- ✅ 清晰目标:“将次日留存率提升5%”
实验策略——具体通过什么方法实现目标。
- ❌ 泛泛策略:“优化用户体验”
- ✅ 具体策略:“通过签到领红包功能,激励用户次日打开App”
数据/调研支持——用数据或用户反馈证明策略的合理性。
- ❌ 主观猜测:“用户可能喜欢红包”
- ✅ 数据支持:“调研显示,60%沉默用户因红包福利回归”
(2)可归因:对照组与实验组仅1个变量差异。
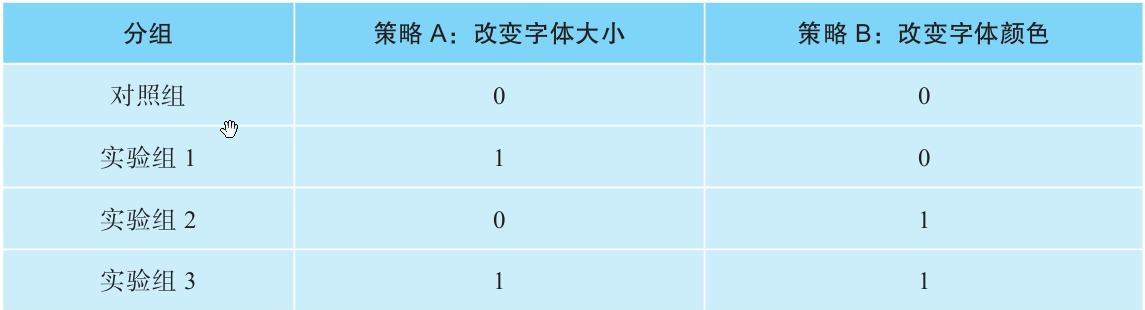
费曼案例:测试字体大小(策略A)和颜色(策略B)时,需设4组(对照+A+B+A+B组合),才能精准归因单一策略效果。
(3)可复用:实验策略能否推广到更多用户、场景或产品,从而放大价值。
- ✅ 能复用:比如优化“登录按钮颜色”可应用于全站所有页面。
- ❌ 不能复用:比如仅针对“北京地区用户”的限时活动。
- 成本效益高:一次实验,多处受益(例:推荐算法优化可复用至所有内容板块)。
- 资源有限:优先做能影响80%用户的实验,而非仅影响5%用户的实验。
- 通用性:策略是否依赖特定条件(如地域、时间段)?
- 潜在影响:覆盖用户量是否足够大?
- 长期价值:是短期活动还是长期功能?
2. 实验设计
(1)样本选择
- 静态抽样:按固定属性(如地域、性别)预先分组,结果可外推全量。
案例:从女性用户中抽10%测试,结果提升5% → 预估全量女性用户提升5%。 - 动态抽样:按行为实时触发(例:进入购物车页用户),结果不可外推。
练习解析:电商价格感知实验应在商品曝光时分流(答案B),确保用户真实参与场景。

(2)指标设计
- 结果指标(终极目标):衡量实验最终效果的核心指标。(如电商:总收入(GMV)、人均消费额;社交App:DAU日活用户数、用户留存率)。
- 过程指标(转化路径):追踪用户行为链路,定位问题环节。(如打开App → 加购 → 发起结账 → 完成结账;关键指标:加购率、结账转化率)。
- 保护指标(风险防控):监控实验可能的负面影响。(如用户流失:卸载率、跳出率;系统性能:页面加载时间、崩溃率;成本控制:优惠券补贴金额)。
电商优惠券实验案例
目标:通过满减优惠券(满50减10)提升总收入。
- 结果指标:
- 人均收入(结账页面曝光用户的人均GMV)
- ROI(总收入 - 优惠券成本)
- 过程指标:
- 各环节转化率(加购率→结账率→支付成功率)
- 保护指标:
- 用户投诉率、App卸载率
关键点:
- 只有看到优惠券的用户(结账页面曝光UV)才是实验真实影响对象。
- 用人均收入而非总收入,避免流量分配不均的干扰。
(3)流量计算
为什么需要计算最小样本量?
- 精度保障:样本量越大,越能检测出细微的效果差异(如0.1%的点击率变化)。
- 置信度:足够的样本量可降低随机波动的干扰,确保结论可靠。
- 案例关联:签到红包实验需240万用户才能检测0.1%的差异,但实际曝光仅60万 → 只能检测≥0.5%的差异。
流量不足的5种解决方案
| 方法 | 适用场景 | 案例中的体现 | 局限性 |
|---|---|---|---|
| 延长实验时间 | 可累计的指标(如总订单数) | 不适用(点击率需按天计算) | 次日留存率等非累计指标无效 |
| 改用低方差指标 | 接受二元指标(如"是否购买") | 用"是否点击"替代"点击次数" | 可能丢失关键信息(如金额差异) |
| 调高检测精度 | 业务允许较大差异(如从0.5%调至1%) | 60万样本只能检0.5%差异,无法检0.1% | 可能漏检小但重要的效果 |
| 过滤用户 | 实验受众不精准(如非目标用户混入) | 仅统计曝光用户(60万),排除未曝光者 | 需确保过滤逻辑不引入偏差 |
| 重启实验 | 其他方法均无效 | 若需检测0.1%差异,需等待流量释放 | 延迟决策时间 |
签到红包实验
- 实验设计:3种红包样式(A/B/C)vs 对照组(D),投放250万用户。
- 关键数据:
- 实际曝光用户仅60万 → 真实样本量=60万(非投放量250万)。
- 最小样本量要求:
- 检测0.5%差异需50万 → 可判断A/B>D,A>C。
- 检测0.1%差异需240万 → 无法判断B vs C或A vs B(差异仅0.1%)。
- 结论:
- 曝光量不足时,小差异(<0.5%)可能被误判为"无差异"。
- 仅曝光用户才计入有效样本(未曝光用户稀释效果)。
Q:为什么250万投放用户中,只有60万算有效样本?
A:因为红包样式仅对实际看到弹窗的用户(曝光量)产生影响,其余190万用户未接触实验策略,属于"噪声数据"。Q:若想证明B样式比C好(差异0.1%),该怎么办?
A:需将曝光量从60万提升至240万(方法:延长实验时间或扩大投放范围)。
(4)实验周期
1. 基础计算公式
公式:实验持续时间 = 最小样本量 / 每日有效用户流入量
案例假设:
- 需检测点击率0.5%差异 → 最小样本量=50万
- 每日进入实验用户=10万
- 理论计算:50万/10万=5天
问题:
- 用户重叠:同一用户可能多日访问(如用户A第1天和第3天都参与),实际独立用户数<50万 → 需延长实验时间。
- 指标特性:次日留存率等指标需按天独立计算,无法简单累计。
2. 关键影响因素与案例
(1) 用户重叠效应
- 案例:某社交App实验每日新增10万用户,但30%为老用户重复访问。
- 第1天:独立用户10万
- 第2天:新增7万独立用户(3万与第1天重叠)
- 实际进度:2天仅获17万独立用户(非20万)→ 需延长至8天达标。
(2) 工作日效应
- 案例:电商App发现:
- 工作日:日均用户8万(白领活跃)
- 周末:日均用户12万(家庭用户激增)
- 对策:至少运行7天(覆盖完整周周期),避免仅用工作日数据导致偏差。
(3) 季节性事件
- 案例:在线教育平台在"开学季"实验:
- 开学前一周:用户活跃度+200%
- 开学后:回归正常
- 风险:若实验仅覆盖开学季,会高估效果 → 需延长至平稳期验证。
(4) 首因效应
- 案例:新按钮设计实验:
- 第1天:点击率+15%(用户好奇)
- 第7天:点击率稳定至+5%
- 结论:需观察至少1周,排除短期干扰。
3. 实验周期设计原则
| 因素 | 应对策略 | 案例应用 |
|---|---|---|
| 用户重叠 | 按独立用户去重计算 | 社交App需从5天延长至8天 |
| 工作日差异 | 覆盖完整周(7天) | 电商实验需包含周末数据 |
| 季节性事件 | 避开大促或延长观测期 | 教育平台避开开学季或对比去年同期 |
| 新奇效应 | 观察指标是否趋于稳定(通常≥7天) | 新按钮点击率需7天后评估真实效果 |
4. 一句话总结
"实验周期≠简单除法,需考虑用户重叠、周期波动和 novelty 效应;宁可多跑3天,不要少看1周。"
案例点睛:
- 若某实验理论需5天,实际应规划7-10天(预留缓冲)。
- 重大策略(如改版)建议运行2周以上,覆盖多个用户行为周期。
3. 实验运行
(1)实验上线
案例背景: 假设“易购”电商App计划上线一个新功能——“购物车底部常驻凑单推荐栏”。该功能会在用户购物车页面底部显示一个固定区域,根据用户购物车内的商品,实时推荐可以凑单满减的商品。目标是提升凑单率和客单价。
1. 实验上线前:准备与检查
(1)检查产品基本流程
案例解释: 产品经理和测试工程师需要模拟用户操作:
将商品加入购物车 -> 进入购物车页面 -> 检查底部推荐栏是否正常显示。
点击推荐栏商品 -> 检查是否能顺利加入购物车 -> 检查加入后推荐栏是否实时刷新。
清空购物车 -> 检查推荐栏是否消失或显示合理提示(如“购物车空空如也,快去逛逛吧”)。
检查在不同网络环境、不同机型下的显示和交互是否正常流畅。
负反馈检查: 重点评估这个固定栏是否遮挡了关键操作(如“结算”按钮)?是否让页面显得过于拥挤?用户是否会觉得推荐过于频繁或打扰?设计上是否清晰告知用户这是凑单推荐?
(2)检查实验设计
1-实验组可分流 & 流量充足
实验计划分3组:A组(对照组,无底部推荐栏)、B组(实验组1,显示推荐栏)、C组(实验组2,显示另一种UI样式的推荐栏)。技术团队需确认:
用户ID分流系统能稳定地将用户随机分配到A/B/C三组(可分流)。
计划给该实验分配总DAU的15%(A/B/C各5%)。易购App日活约2000万,5%流量即约100万用户/组/天。这个量级对于观察凑单率、客单价等核心指标的变化是足够的(流量充足)。
2-实验指标可计算 & 埋点数据上报
核心指标
凑单率: (点击推荐栏商品并加入购物车的用户数) / (看到推荐栏的用户数)。需要埋点:推荐栏曝光、推荐栏内商品点击、商品加入购物车(需标记来源为“凑单推荐”)。
客单价变化: 实验组 vs 对照组用户平均订单金额差异。需要依赖现有下单金额埋点。
购物车页停留时长: 可能受新元素影响。
检查点
新增埋点: 确认前端工程师已为“推荐栏曝光”、“推荐栏商品点击”(需记录点击的商品ID和位置)、“从推荐栏加入购物车”(需打上特定来源标记)等事件完成埋点代码开发并测试通过。
字段规范: 确认埋点上报的字段(如
event_name=cart_recommend_click,item_id=xxx,position=yyy,source=zzz)符合数据团队的规范。存储与计算: 确认数据仓库已准备好接收这些新事件,数据团队已开发好ETL Pipline,能将原始日志清洗、转换并写入分析数据库(如Hive表),且下游BI报表或实验平台能正确读取并计算上述指标。确认数据保留时间满足实验分析需求(通常至少保留实验期+后续一段时间)。
2. 实验上线后:验证与监控
(1)个体校验:白名单体验 & 日志抓包
白名单
将测试账号加入B组(实验组)白名单。
登录测试账号 -> 添加商品到购物车 -> 进入购物车页面 -> 肉眼可见: 底部是否出现了推荐栏?样式是否正确?推荐的商品是否相关?点击商品是否能加入购物车?加入后推荐栏是否刷新?功能交互是否顺畅?
日志抓包
对于用户不可见的逻辑,比如“推荐算法是否真的为B组用户启用了新策略”?仅靠UI无法完全确认。
技术同学在测试账号操作时,抓取其设备与服务器的网络请求日志。
在日志中搜索关键API请求(如获取购物车信息的请求)。检查服务器返回的响应数据中,是否包含了新设计的推荐栏数据字段(如
has_bottom_recommend: true,recommend_items: [...])。这证明后端逻辑确实为该用户(B组)启用了新策略。
(2)实验指标监控
a. 用户数量符合分流预期
百分比分流
实验上线后第一天(完整天),查看实验平台数据:进入A、B、C三组的用户数应各在100万左右(2000万 * 5%)。如果发现B组只有70万,C组有130万,偏差 = (130-100)/100 = 30%, 远超合理范围(通常<5%可接受)。这必须立刻报警!需要检查:分流服务配置是否错误?用户属性(如新老用户)是否在组间严重不均衡?实验配置是否被意外修改?
版本折损: (假设此功能依赖App新版本)
实验上线首日,新版本覆盖率仅20%。
理想每组100万用户进入实验,但实际每组只有 100万 * 20% = 20万用户(因为只有升级了新版本的用户才有机会触发新功能逻辑)。这是正常现象,并非实验下发问题。随着新版本覆盖率提升(比如一周后到80%),每组用户数会逐渐接近80万。分析数据时,要基于已升级新版本的用户来看效果。
b. 指标符合产品常识 & 核心指标监控
埋点数据校验
查看B组(有推荐栏)的数据:
“推荐栏曝光”事件量:是否与进入购物车页面的用户量大致匹配?(如果100万用户进入购物车,曝光量也应接近100万)。
“推荐栏商品点击”事件量:是否远小于曝光量?(正常,不是每个人都会点)。
“从推荐栏加入购物车”事件量:是否小于点击量?(正常,点击后可能不加车)。
转化率检查: 点击率(点击/曝光)假设是5%,加入购物车率(加车/点击)假设是30%。如果发现点击率高达80%或加车率低至1%,明显不符合常识!可能原因:埋点上报错误(如曝光事件重复上报)、推荐算法失效(推荐了完全无关或劣质商品)、UI设计有误导性(用户误点)。
核心指标监控
监控B组、C组(实验组)的凑单率、客单价、购物车页停留时长,并与A组(对照组)对比。
同时监控: B/C组的人均订单数、App整体人均停留时长、核心页面(如首页、商详页)的转化率等大盘核心指标。为什么? 虽然目标是提升凑单和客单,但新功能可能带来副作用:
推荐栏是否让用户觉得烦扰,导致购物车页跳出率升高?
是否因为凑单推荐太强,用户反而犹豫不决,降低了整体下单率?
新功能是否增加了App的资源消耗,导致卡顿,影响整体体验?
特殊群体差异注意: 如果这个实验只针对老用户(比如注册>30天的用户),那么B/C组用户的历史购买频次、客单价基线本身就可能远高于大盘平均值(包含大量新用户和低频用户)。直接拿B/C组的客单价与大盘比没有意义,重点是比较B/C组 vs A组(同为老用户)的差异。
c. 组间数据差异符合预期 & 均匀性检验
AA/BB组校验
在本次实验中,虽然目标是测试B/C两种新样式,但为了检验分流均匀性,可以设置:
A1组(对照组1,5%流量,无推荐栏)
A2组(对照组2,5%流量,无推荐栏)-> 这就是AA组
B1组(实验组1,5%流量,推荐栏样式1)
B2组(实验组2,5%流量,推荐栏样式1)-> 这就是BB组 (测试样式1的均匀性)
C组(实验组3,5%流量,推荐栏样式2)
检查
A1组 和 A2组 的各项核心指标(凑单率、客单价等)差异是否很小(在统计误差范围内)?如果A1的凑单率比A2显著高很多,说明分流不均匀!可能是用户分配不随机,导致A1组用户本身就更爱凑单。这会严重质疑后续B/C组与A组比较结果的可信度。
同理,B1组 和 B2组 的各项指标也应非常接近。如果差异显著,说明实验处理(样式1)的下发或数据采集可能有问题。
意义: AA组/BB组之间的差异是衡量实验基础环境(分流、数据采集)是否可靠的“金标准”。如果AA差异大,整个实验结论都不可信。
总结
通过“易购App购物车底部凑单推荐栏”这个案例,我们可以看到AB实验从上线前严谨的流程、逻辑、埋点、数据基建检查,到上线后即时的个体功能验证(白名单/抓包) 和核心的数据指标监控(用户量校验、常识校验、核心指标监控、组间均匀性校验) 的全过程。每一步都是为了确保实验能够正确运行、收集的数据准确可靠,最终得出的实验结论(哪种方案更好)是科学可信的,从而为产品决策提供坚实依据。忽略任何一步,都可能导致实验失败、得出错误结论,甚至对线上用户体验和业务指标造成负面影响。
(2)实验停止条件 & 常见问题应对
在A/B测试中需要立即停止实验的三种关键信号:实验异常、明显负反馈、大幅负向效果,以及三种实验中常见的问题及其应对策略:预设精度过高、增量扩量风险、数据大幅波动。
实验停止条件
实验异常: “小A,想象我们在测试一个新按钮颜色。上线后发现,实验组用户压根没看到新按钮(比如技术bug导致按钮没加载出来),或者对照组用户反而被错误地分配到了新按钮。这时数据肯定乱七八糟,不能反映真实效果。这就好比做化学实验,试管裂了或者加错了试剂,必须马上停下,修好设备重新开始。”
明显负反馈: “假如我们测试一个更激进的广告策略。上线后,用户投诉激增,社交媒体上都在骂我们骚扰用户,品牌形象受损了。这时就算数据还没出结果,也必须立刻停下!这就像你开了一家新口味的奶茶店试营业,结果顾客喝了纷纷吐槽难喝甚至拉肚子,网上差评如潮,你还能继续卖吗?肯定得先关门,搞清楚问题出在哪(配方?原料?),再决定是彻底放弃这个口味还是改进后再试。”
大幅负向效果: “这个情况是实验本身运行正常,流量分配、用户行为都符合预期,实验也运行了足够长时间(数据平稳)。但结果发现核心指标(比如用户购买率、公司收入)大跌!除非这个下跌是我们策略故意设计的(比如测试一个减少促销的策略,预期短期收入会降但长期用户忠诚度会升),否则必须立即刹车。就像你给汽车换了个新引擎,试车跑了足够里程,结果发现油耗飙升了50%,动力还下降了。这肯定不是预期结果,得马上停下来检查引擎是不是有缺陷。”
常见情况及应对
预设精度过高: “小A,我们计划做实验前会算需要多少用户(样本量)。但如果算的时候要求太高(比如非要检测出0.1%的微小提升),结果实验跑完了,发现业务上确实有提升(比如转化率涨了1%),但因为预设精度要求太苛刻,统计上显示‘不显著’。这就等于你买了个超级精确的秤,想称一粒米的重量变化,结果秤的误差都比米粒的变化大,当然称不出来。应对办法就是:要么接受这个提升(如果业务上足够重要),要么重新设计实验,要么延长实验时间收集更多数据(相当于换个没那么‘灵敏’但能测出1%变化的秤)。”
增量扩量风险: “有时候为了省时间,实验人员会在原有5%流量实验的基础上,直接再加5%流量进去(变成10%)。这听起来省事,但其实隐藏两个大坑:一是新加的用户进来会引起数据波动(就像往平静的池塘里扔石头),需要重新等待数据稳定,这时间可能比重新开个10%流量的实验还长;二是新旧用户混在一起,万一新用户群和老用户群本身有差异(比如渠道不同),或者分流系统在新流量上出问题,你很难区分到底是策略效果还是流量不均导致的。这就好比你做蛋糕,第一次按A配方做了小份(5%流量),觉得不错想做大份。错误做法是把A配方小份蛋糕掰碎,再混入按A配方新做的大份蛋糕糊(增量扩量),然后一起烤。烤出来味道不对,你根本分不清是小份蛋糕放久了变味了,还是新蛋糕糊比例错了,还是烤箱温度不均。正确做法是干脆按A配方单独新做一个完整的大蛋糕(重新分配10%流量)。除非是为了让同一用户始终体验一致(比如界面改版),否则最好别增量扩量。”
数据大幅波动: “实验期间遇到双十一、系统故障、明星八卦热搜这种大事,用户行为会剧烈变化,数据像坐过山车。这时数据的‘噪音’(方差)变大了,原来估算的样本量可能就不够了。就像在大风天测量旗杆高度,风把测量工具吹得晃来晃去(方差大),你测一次的结果可能很不准。你需要测很多次(相当于需要更大样本量)或者等风停(波动结束)才能测准。实验平台能剔除特殊时段数据当然好,但像双十一这种影响深远的事件(‘日历效应’),用户购物习惯可能几周都受影响,而且很难区分是活动影响还是实验策略影响。应对核心是:预防为主,避开可预见的大波动期(如春节、大促)。万一撞上了,最可靠的办法是拉长实验时间,收集更多数据,让波动被‘平均’掉,或者等影响完全过去再分析。”
简化类比
实验停止条件 = 开车警示灯:
异常灯(实验异常): 仪表盘乱跳/发动机故障灯亮 -> 立即靠边停车检查。
投诉风暴灯(明显负反馈): 乘客集体呕吐/强烈抗议 -> 立即停车安抚,检查是不是车有问题。
性能暴跌灯(大幅负向效果): 油耗猛增/动力锐减 -> 立即停车检查,除非你故意在测试“省油模式”(牺牲动力)。
常见问题应对:
预设精度过高 = 用显微镜看大象: 工具太灵敏,反而看不到整体变化。换放大镜(调整检测目标)或者站远点看(延长实验/接受业务显著性)。
增量扩量 = 新旧颜料混用: 想省颜料,把旧颜料桶里剩下的倒进新颜料桶里混合用。结果画出来颜色不对,你搞不清是旧颜料变质了还是新颜料配方错了。不如直接开一桶新颜料(重新分配流量)。
数据大幅波动 = 大风天测旗杆: 风大(外部事件)导致测量工具(数据)剧烈晃动(方差大)。要么多测几次取平均(增大样本量/延长实验),要么等风停(避开或等待特殊时期结束)。
总结:
停止实验是果断止损的关键机制, 针对三种严重风险(无效实验、用户反感、核心伤害)设置明确的“熔断点”。
实验设计需务实: 样本量计算要符合实际业务需求,避免过度追求统计显著性而忽略业务显著性。
“省事”可能更费事: 增量扩量看似快捷,实则引入混淆变量和等待成本,风险大于收益,应尽量避免。
数据质量是生命线: 外部冲击会严重干扰实验结果识别。核心策略是“避”大于“治”:优先避开已知波动期。若无法避免,则需显著延长实验时间或利用平台功能谨慎处理数据,充分认识到重大事件的持续影响(日历效应)。
(4)实验放量风险
1. 概念:明确你要学习的是什么?
核心概念1:实验放量 (Experiment Rollout/Ramp-up):将实验策略(比如新的算法、功能、内容策略)逐渐应用到更大比例的用户群体上的过程。原因可能是样本量不足或初步效果正向。
核心概念2:辛普森悖论 (Simpson's Paradox):当把来自不同群体或不同条件(如不同放量阶段)的数据合并分析时,数据展现的趋势(如实验组更好/更差)可能与每个子群体/子阶段内的实际趋势完全相反。关键在于分组权重(比例)的变化。
案例背景:某资讯产品做了一个实验,将A类内容(点击率较高的内容)在列表中的曝光占比提升了(实验组)。关心的核心指标是整体点击率(CTR)。实验后观察到的现象是:A类内容的CTR下降了,B类内容的CTR也下降了。这看起来实验效果是负面的?但合并数据后发现整体CTR提升了?为什么?
2. 教授:假装把这个概念教给一个小学生或外行
解释放量(简单版):想象我们在学校小卖部测试一种新口味糖果。第一天只给10个同学试吃(实验组),其他90个同学吃原来的糖果(对照组)。如果试吃的10个同学都说好吃,我们可能第二天让50个同学都试吃新糖果(放量了),剩下50个吃原来的。
解释辛普森悖论(用糖果案例类比):
第一天(小范围放量10%):试吃新糖果的10个同学,8个说好吃(好吃率80%)。吃旧糖果的90个同学,63个说好吃(好吃率70%)。新糖果看起来更好!
第二天(放量到50%):试吃新糖果的50个同学,35个说好吃(好吃率70%)。吃旧糖果的50个同学,30个说好吃(好吃率60%)。新糖果还是更好!
合并两天数据(错误方式):
新糖果总好吃次数:8(第1天) + 35(第2天) = 43次。总试吃人数:10 + 50 = 60人。合并好吃率 = 43 / 60 ≈ 71.7%
旧糖果总好吃次数:63(第1天) + 30(第2天) = 93次。总试吃人数:90 + 50 = 140人。合并好吃率 = 93 / 140 ≈ 66.4%
结论:新糖果(71.7%) > 旧糖果(66.4%),看起来还是新糖果好。
发现问题(辛普森悖论出现):等等!我们明明看到每一天新糖果都比旧糖果好吃(80%>70%, 70%>60%),合并后(71.7%>66.4%)也显示新糖果好,这好像没悖论啊?哪里错了?
关键点(权重变化):错在合并掩盖了结构变化。第一天只有10%的人吃新糖(好吃率高80%),第二天有50%的人吃新糖(好吃率降到70%)。当我们简单合并两天数据时,第二天(好吃率较低但占比大增)的数据拉低了新糖的总好吃率。同时,旧糖第一天占90%(好吃率70%),第二天只占50%(好吃率60%),第二天(好吃率较低但占比大减)的数据没有像新糖那样显著拉低旧糖的总好吃率。结果就是,新糖的总好吃率(71.7%)虽然还是比旧糖(66.4%)高,但这个优势(71.7% - 66.4% = 5.3%)比第一天观察到的优势(80%-70%=10%)和第二天(70%-60%=10%)都要小得多!如果权重变化更极端,甚至可能出现合并后优势消失或反转(真正的悖论)。案例2属于优势被合并稀释(但未反转),是辛普森悖论原理的体现(权重变化影响合并结果),展示了合并可能扭曲对效应大小的判断。
3. 回顾:检查理解中的漏洞,回到原始材料
回顾案例数据
对照组 (旧策略): A曝光占比10%, CTR=20%; B曝光占比90%, CTR=5%; 整体CTR = (10% * 20%) + (90% * 5%) = 2% + 4.5% = 6.5%
实验组 (新策略:A提权): A曝光占比50%, CTR=15%; B曝光占比50%, CTR=4%; 整体CTR = (50% * 15%) + (50% * 4%) = 7.5% + 2% = 9.5%
观察现象:A的CTR从20%降到15%, B的CTR从5%降到4%。但整体CTR从6.5%升到了9.5%!
解答问题 :
实验提升了整体的点击率吗? 是的!整体CTR从6.5%提升到了9.5%。
为什么A、B的点击率都下降?
A类下降 (15% < 20%):因为实验组把A的曝光占比大幅提高(从10%到50%)。想象一下,原来列表里10条信息只有1条是A类(精品),用户看到会眼前一亮去点。现在列表里10条信息有5条都是A类(精品),用户可能觉得“怎么都是这种?有点腻/不稀罕了”,或者精品内容本身供应质量跟不上突然增加的需求(边际效应递减),导致A类本身的吸引力相对下降(CTR下降)。简单说:好东西一下子给太多,大家反而不那么珍惜了。
B类下降 (4% < 5%):因为A类曝光占比大增,挤占了B类的曝光空间(从90%降到50%)。原来用户浏览时,大部分时间看到的是B类,偶尔看到A类精品会点。现在用户一半时间都在看A类(即使CTR降了,但15%仍远高于B的5%),用户有限的注意力和点击更多地被A类吸引走了,留给B类的关注和点击自然就变少了(CTR下降)。简单说:精品抢走了普通品的风头和点击机会。
这种提升点击率的方法可能有什么潜在问题?
用户体验单一化/疲劳: 过度依赖高CTR内容(A类)可能导致信息茧房或内容同质化,用户容易感到厌倦,长期留存可能下降。就像天天吃山珍海味也会腻。
牺牲内容多样性/生态健康: 过度挤压B类内容的曝光,可能让优质但CTR相对不突出的B类内容(如深度报道、小众兴趣)失去生存空间,破坏平台内容生态的多样性和健康度。
依赖“低质”高CTR内容风险: 如果A类内容的高CTR是靠标题党、低俗、猎奇等“不良”手段获得的,这种提升方式损害平台长期价值和品牌形象,不可持续。
指标单一陷阱: 只关注整体CTR提升,可能掩盖了其他重要指标的恶化,比如用户阅读时长、分享率、满意度、留存率等。用户可能点了很多A类,但很快就关掉了(阅读深度浅)。
辛普森悖论的警示: 这个案例本身展示了只看分项指标(A CTR降, B CTR降)会得出错误结论(实验负向),而合并计算整体指标(整体CTR)才反映真实效果(正向)。这提醒我们在分析实验,尤其是涉及流量分配变化(放量)或用户群体结构变化时,必须谨慎选择分析维度(整体 vs 分层),警惕辛普森悖论。 放量过程中流量分配比例的变化,是诱发辛普森悖论的高风险场景。
4. 简化:用最简洁清晰的语言概括核心
实验放量:好实验初步验证后,逐步开放给更多用户用。
辛普森悖论陷阱:在放量时,如果不同阶段或不同用户群的实验/对照组比例变化很大,简单合并所有数据来看实验效果好坏,可能会得出完全错误或者严重失真的结论(比如把好效果算小了,甚至误判成坏效果)。
案例核心解释:
实验通过大幅增加高点击率(A类)内容的曝光占比来提升整体点击率。
A类CTR下降:因为一下子给太多,用户不觉得稀罕/内容跟不上。
B类CTR下降:因为A类抢走了用户的注意力和点击。
整体CTR上升:因为用户点得更多的A类(虽然效率降了点)取代了大量用户不怎么点的B类。高点击率内容占据的版面大幅增加是主因。
潜在问题:
用户可能看腻(单一化)。
其他内容被挤压死(生态破坏)。
可能鼓励了坏内容(标题党)。
可能只看点击率,忽略了其他重要指标(短期主义)。
放量分析时,必须注意流量结构变化,防止辛普森悖论误导判断。
总结:这个案例生动地展示了实验放量过程中辛普森悖论的威力。它告诉我们:
合并数据需谨慎: 当实验组/对照组的流量分配比例在放量过程中发生变化时,直接加总所有数据评估实验效果是危险的,可能严重低估甚至颠倒真实的效应。
理解现象背后的“为什么”: A/B类CTR双降但整体CTR提升,根源在于曝光结构的巨大改变(A占比激增) 和用户注意力的竞争(A抢B的点击)。高CTR的A类获得了不成比例的巨大曝光增量,是整体提升的关键驱动力。
指标选择与长期视角: 单纯追求整体CTR提升可能带来内容生态恶化和用户体验下降等长期风险。需要结合多样性、用户满意度、留存率等综合指标评估。
4. 实验分析
(1)明确影响范围
- 只分析真正受策略影响的用户。
案例:购物车优惠券实验应分析打开购物车页的用户(非全站用户),避免未曝光用户稀释效果(表16-6)。
(2)确保组间可比性
- 避免幸存者偏差:不直接对比"点击弹窗用户" vs "未点击用户"(本身行为差异大)。
(3)维度细分
- 按设备、时段、用户类型等细分,发现隐藏洞见。
费曼案例:深夜时段(0-3点)用户消费时长提升显著 → 针对性优化该时段内容推荐(图16-2)。
(4)统计学解读
- P值<0.05:拒绝原假设(效果显著)
- P值>0.05且功效>0.8:大概率无差异
练习解析:- 实验效果置信区间[0.0025, 0.0499]且提升5% → 统计与业务均显著(答案A)
5. 实验决策
(1)决策依据
- 核心指标是否达预期(需提前定义业务显著性)
- 成本收益权衡(开发/维护成本 vs 收益)
- 负面影响的容忍度(如DAU提升但收入下降)
(2)三种结果
- 发布:效果正向且保护指标达标(例:实验组2红包策略ROI最优 → 放量至95%)
- 下线:核心指标负向或用户投诉激增
- 重新实验:效果不显著或实验条件未满足
(3)实验报告要素
- 背景目标 → 方案设计 → 数据分析 → 结论与后续计划
三、关键方法论提炼
| 环节 | 核心思维 | 避坑指南 |
|---|---|---|
| 实验假设 | 目标先行,避免盲目探索 | 拒绝"大海捞针式实验" |
| 实验设计 | 流量均匀,指标分层监控 | 动态抽样结果不可外推全量 |
| 实验分析 | 归因到人,细分维度找洞见 | 警惕幸存者偏差和辛普森悖论 |
| 实验决策 | 平衡统计显著与业务价值 | 成本过高时需更高收益覆盖 |
