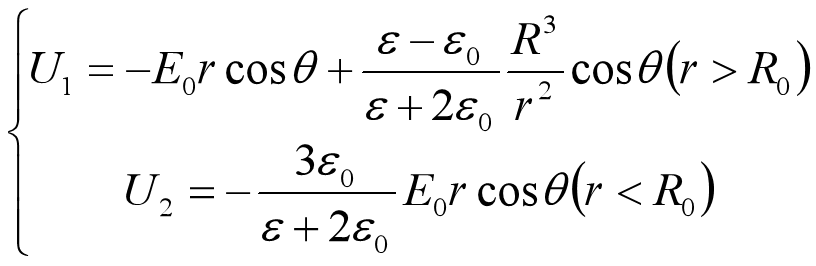电动力学问题中的Matlab可视化
电磁场的经典描述
小说一则
- 电磁场的经典描述就是没有啥玩意量子力学的经典电动力学下对电磁场的描述,以后有空写个科幻小说,写啥呢,就写有天张三遇见了一个外星人,外星人来自这样一个星球,星球上的物质密度特别低,导致外星人的测量会明显的影响物质的运动,外星人不能同时得到动量与位置啊啥的......
- 外星人很希望有一天能找到一个不那么量子力学的世界(这依然是经典的"量子观")
- 张三是个优秀的气象工作员,搞出来的全是李雅普诺夫不稳定的数学模型
- 张三见了外星人表示很好,咱们臭味相投啊
- 外星人表示,是的,学数学物理,物理数学有啥意思呢,不如享受当下的生活
- 张三表示,好哇好哇,好个锤子哇,我们要探索宇宙,你不觉得李雅普诺夫的理论很过时吗,不够先进啦
- 外星人表示:我说一个像是反驳了但是没有成功反驳的话啊:李雅普诺夫是苏俄时期逝世的
- 张三表示:...........
- 外星人表示:还是要好好学习哇!
四个方程组
麦克斯韦方程组
电磁物质方程组
电磁边值方程组
势场边值方程组
电势
库伦规范下的磁矢势
(旋度的旋度=散度的散度-拉普拉斯算子)
磁标势
数据可视化
重要提示
- 不论是数据可视化还是数值计算
- 都不可能替代你的理论分析过程
- 永远是你先得到了一个差不多的结果,才去做数值分析,可视化等等。
- 数据可视化常常受限于你的计算机和人眼
- 不要太较真
常见绘图语言
- 一些常见符号不再赘述
流线 Streamlines
将矢量平滑得连接起来的不相交的曲线
matlab代码----Copyright 2015 The MathWorks, Inc.
[x,y] = meshgrid(0:0.1:1,0:0.1:1);
u = sin(x);
v = -cos(y);figure
quiver(x,y,u,v)startx = 0.1:0.1:1;
starty = ones(size(startx));
streamline(x,y,u,v,startx,starty)matlab 语法
streamline(X,Y,Z,U,V,W,startx,starty,startz)
streamline(U,V,W,startx,starty,startz)
streamline(XYZ)
streamline(X,Y,U,V,startx,starty)
streamline(U,V,startx,starty) 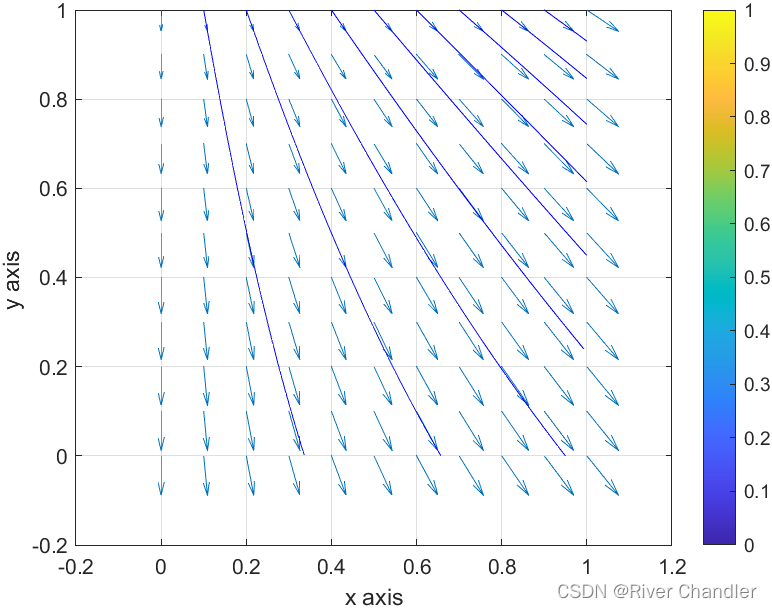
等值线
连接值相等的多个点的不相交的封闭曲线
x = linspace(-2*pi,2*pi);
y = linspace(-2*pi,2*pi);
[X,Y] = meshgrid(x,y);
Z = tan(X)-cos(Y);
contour(X,Y,Z)
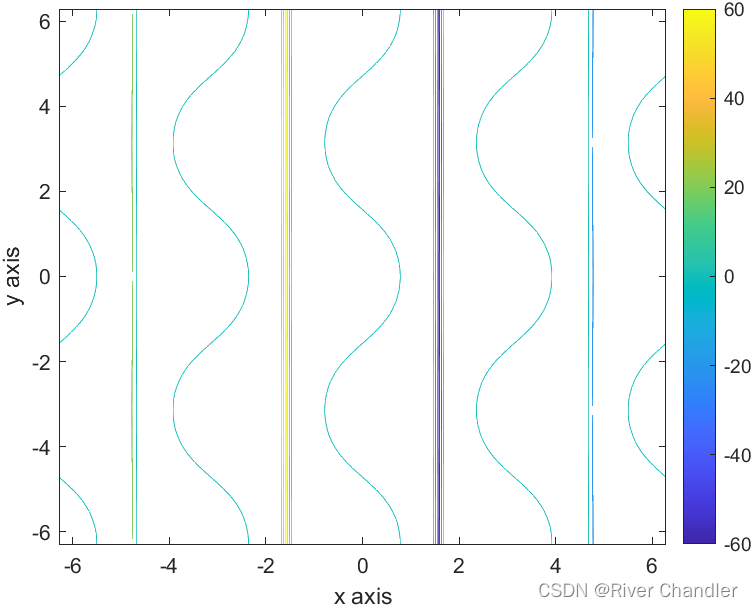
matlab 语法
contour(X,Y,Z,'线型',等高线表示的值)数据可视化案例一:匀强电场中的电导体球

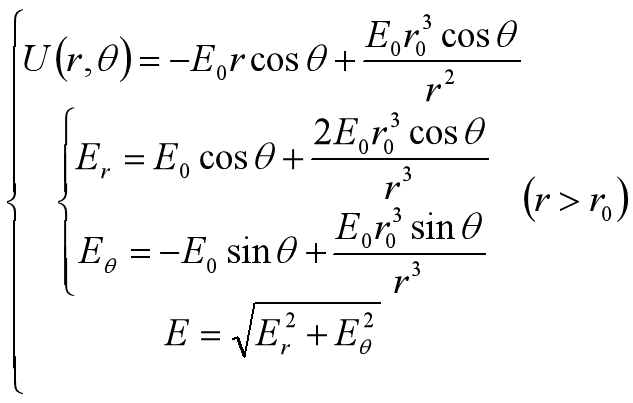
数据可视化案例二:匀强电场中的电介质球