46-堆
目录
1.概念
2.表示
3.三大操作
4.代码实现最大堆(基于数组,编号从0开始)
4.1.根据孩子节点k获取当前父节点的索引
4.2.根据父节点k求左孩子节点下标
4.3.根据父节点k求右孩子节点下标
4.4.判空
4.5.toString()方法
4.6.判断数组中元素是否有序
4.7.查看堆顶元素
4.8.交换当前数组中 i 和 parent 的值
4.9.将value存储在堆中
4.10.元素上浮操作
4.11.取出当前堆的最大值,继续调整堆
4.12.元素下沉操作
4.13.heapify堆化操作:将任意给定的整型数组调整为堆
4.14.测试
5.总代码实现
6.总结
1.概念
- 逻辑上是一棵完全二叉树,物理上是保存在数组中。
- 基于二叉树的堆叫二叉堆。(堆的实现基本都是二叉树,还有其他的,少)
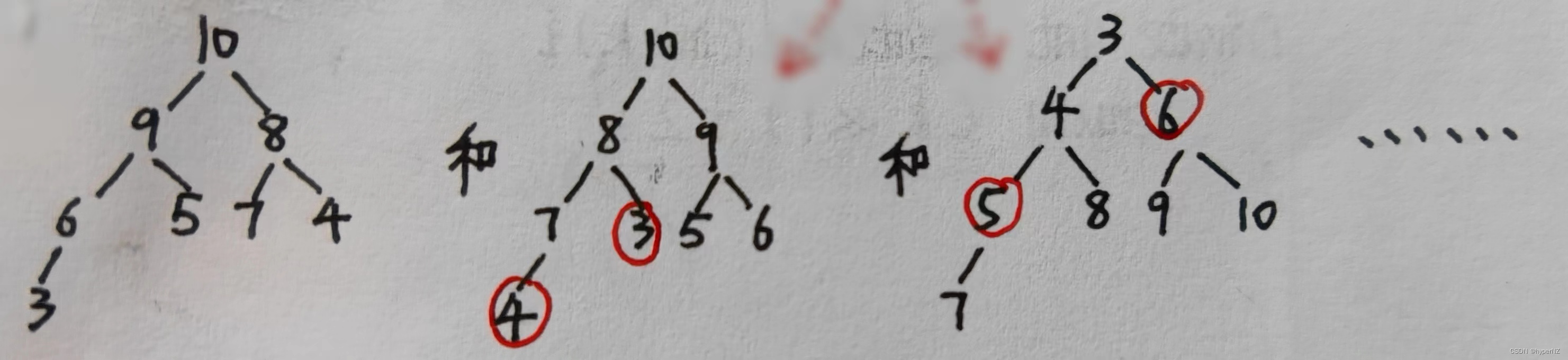
- 从节点值的要求来看,分为:
- 最大堆(Java中的叫法)/大根堆(C++中的叫法):堆中根节点的值 >= 左右子树节点值。
- 最小堆/小根堆(JDK优先级队列就是小根堆):堆中根节点的值 <= 左右子树节点值。
- 左右子树仍满足此性质。
注:
- 最大/小堆的节点大小关系与节点高度无关!
- 相同的数据下,可能有不同种类的堆,例:可有最大堆构建,也可有最小堆构建。
- 二分搜索树比堆的节点值大小关系要求更严格。
2.表示
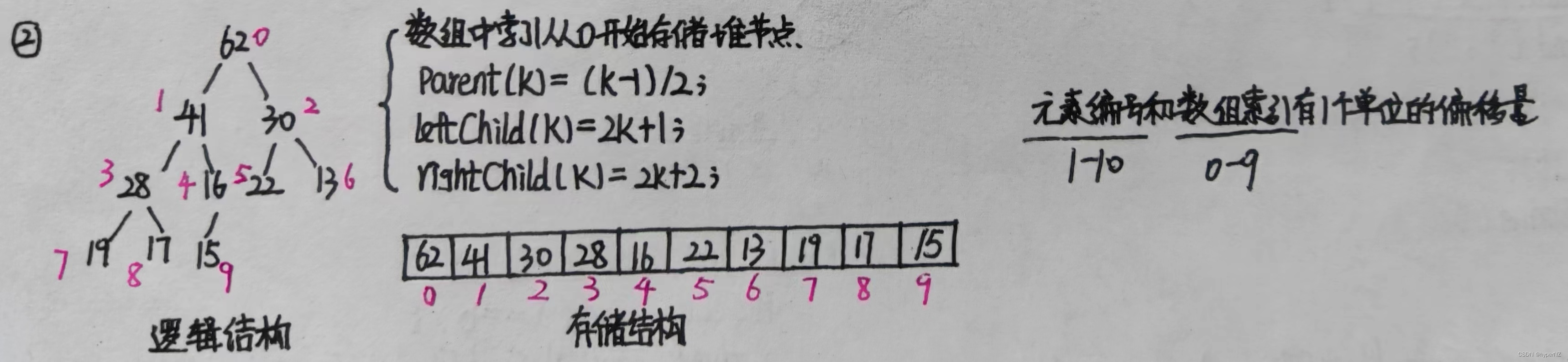
用数组表示(动态数组可扩容),编号表示结构。(2种)
①

②
3.三大操作
- add:向堆末尾添加元素。PS:siftUp元素上浮。
- extractMax:取出当前堆的最大值元素。PS:siftDown元素下沉。
- heapify:堆化(将任意给定的整型数组调整为堆)。PS:siftDown元素下沉。
4.代码实现最大堆(基于数组,编号从0开始)
4.1.根据孩子节点k获取当前父节点的索引
/*** 根据孩子节点k获取当前父节点的索引* @param k* @return*/
private int parent(int k) {return (k - 1) >> 1; //位运算符比除法要快 return (k - 1) / 2;
}4.2.根据父节点k求左孩子节点下标
/*** 根据父节点k求左孩子节点下标* @param k* @return*/
private int leftChild(int k) {return ( k << 1 ) + 1; //2k + 1
}4.3.根据父节点k求右孩子节点下标
/*** 根据父节点k求右孩子节点下标* @param k* @return*/
private int rightChild(int k) {return (k << 1) + 2; //2k + 2
}4.4.判空
/*** 判空* @return*/
public boolean isEmpty() {return data.size() == 0;
}4.5.toString()方法
@Override
public String toString() {StringBuilder sb = new StringBuilder();sb.append("[");for (int i = 0; i < data.size(); i++) {sb.append(data.get(i));if(i != data.size() - 1){sb.append(",");}}sb.append("]");return sb.toString();
}@Override
public String toString() {return data.toString();
}4.6.判断数组中元素是否有序
/*** 判断数组中元素是否有序* @param arr* @return*/
public static boolean isSorted(int[] arr) {for (int i = 0; i < arr.length - 1; i++) { //i < arr.length - 1走不到最后一个元素,arr.length - 1是最后一个元素if(arr[i] < arr[i + 1]) {return false;}}return true;
}4.7.查看堆顶元素
/*** 查看堆顶元素* @return*/
public int peekHeap() {if(data.size() == 0) {throw new NoSuchElementException("heap is empty!");}return data.get(0);
}4.8.交换当前数组中 i 和 parent 的值
/*** 交换当前数组中 i 和 parent 的值* @param i* @param parent*/
private void swap(int i, int parent) {int tmp = data.get(i);int parentVal = data.get(parent);data.set(i,parentVal);data.set(parent,tmp);
}4.9.将value存储在堆中
/*** 将value存储在堆中* @param value*/
public void add(int value) {//1.向数组末尾添加元素this.data.add(value);//2.调整当前堆的结构,使其仍然满足最大堆的性质siftUp(data.size() - 1);
}4.10.元素上浮操作
/*** 元素上浮操作* @param i 要上浮的元素索引*/
private void siftUp(int i) {while(i > 0 && data.get(i) > data.get(parent(i))) {swap(i,parent(i));//继续向上判断交换后父节点向上的节点关系i = parent(i);}
}4.11.取出当前堆的最大值,继续调整堆
/*** 取出当前堆的最大值,继续调整堆* @return*/
public int extractMax() {//判断当前堆是否为空if(data.size() == 0) {throw new NoSuchElementException("heap is empty!");}int max = data.get(0);//将最后一个元素顶到堆顶int lastElement = data.get(data.size() - 1);data.set(0, lastElement);//删除最后一个元素data.remove(data.size() - 1);//元素下沉siftDown(0);return max;
}4.12.元素下沉操作
/*** 元素下沉操作* @param i 要下沉的元素索引*/
private void siftDown(int i) {//终止条件:当i还有子树时,说明还没判断结束;若左孩子都不存在,则一定不存在右孩子while(leftChild(i) < data.size()) {//此时i索引对应的元素仍然存在左子树,没到叶子节点int j = leftChild(i);//此时还存在右子树if(j + 1 < data.size() && data.get(j + 1 ) > data.get(j)) {//此时右子树的值大于左子树j = j + 1;}//j一定保存了左右子树的最大值索引if(data.get(i) >= data.get(j)) { //此处为何是 >=//如果此处终止条件是 父节点 > 子节点,也可以,不会死循环//以后在写测试用例时,必须要复杂//此时i对应的元素已经下沉到合适位置break;}else{swap(i,j);i = j;}}
}4.13.heapify堆化操作:将任意给定的整型数组调整为堆
/*** heapify堆化操作:将任意给定的整型数组调整为堆* ①自底向上逐渐调整堆的过程,只看非叶子节点,从最后一个非叶子节点(最后一个非叶子节点就是最后一个节点他爸)开始,一次性砍掉所有叶子节点,进行元素的siftDown操作,直到向上走到根节点即可,时间复杂度为O(n)* ②遍历原数组,依次add操作,时间复杂度为O(nlogn)* @param arr*/
public MaxHeap(int[] arr) {//初始化data = new ArrayList<>(arr.length);//1.先将arr的所有元素拷贝到data中for(int i : arr) {data.add(i);}//2.从最后一个非叶子节点开始进行元素下沉for (int i = parent(data.size() - 1); i >= 0 ; i--) {siftDown(i);}
}4.14.测试
public static void main(String[] args) {
// MaxHeap heap = new MaxHeap();
// heap.add(5);
// heap.add(2);
// heap.add(7);
// heap.add(1);
// heap.add(3);
// System.out.println(heap);
//
// int[] ret = new int[5];
// for (int i = 0; i < ret.length; i++) {
// ret[i] = heap.extractMax();
// }
// System.out.println(Arrays.toString(ret));// int[] data = {17,90,68,12,15,14,70,30,20};
// MaxHeap heap = new MaxHeap(data.length);
// //依次调用extractMax()->集合恰好是一个降序集合
// for (int i = 0; i < data.length; i++) {
// heap.add(data[i]);
// }
// for (int i = 0; i < data.length; i++) {
// data[i] = heap.extractMax();
// }
// System.out.println(Arrays.toString(data));// int[] data = {17,90,68,12,15,14,70,30,20};
// MaxHeap heap = new MaxHeap(data);
// //依次调用extractMax()->集合恰好是一个降序集合
// for (int i = 0; i < data.length; i++) {
// data[i] = heap.extractMax();
// }
// System.out.println(Arrays.toString(data));int n = 10000;int[] data = new int[n];//生成随机数Random random = new Random();for (int i = 0; i < n; i++) {//范围是 0 - Integer.MAX_VALUEdata[i] = random.nextInt(Integer.MAX_VALUE);}MaxHeap heap = new MaxHeap(data);for (int i = 0; i < n; i++) {data[i] = heap.extractMax();}System.out.println(isSorted(data));
}5.总代码实现
import java.util.*;/*** 基于数组实现的最大堆* 编号从0开始,假设当前节点为i,i>0* parent = (i - 1) / 2;* 若有左右孩子,保证 2i + 1 或 2i + 2 < data.length;* left = 2i + 1;* right = 2i + 2;*/
public class MaxHeap {//具体存储元素的动态数组private List<Integer> data;//无参构造public MaxHeap() {this(10);}//指定容量大小public MaxHeap(int initCap) {this.data = new ArrayList<>(initCap);}/*** 根据孩子节点k获取当前父节点的索引* @param k* @return*/private int parent(int k) {return (k - 1) >> 1; //位运算符比除法要快 return (k - 1) / 2;}/*** 根据父节点k求左孩子节点下标* @param k* @return*/private int leftChild(int k) {return ( k << 1 ) + 1; //2k + 1}/*** 根据父节点k求右孩子节点下标* @param k* @return*/private int rightChild(int k) {return (k << 1) + 2; //2k + 2}/*** 判空* @return*/public boolean isEmpty() {return data.size() == 0;}@Overridepublic String toString() {return data.toString();}/*** 判断数组中元素是否有序* @param arr* @return*/public static boolean isSorted(int[] arr) {for (int i = 0; i < arr.length - 1; i++) { //i < arr.length - 1走不到最后一个元素,arr.length - 1是最后一个元素if(arr[i] < arr[i + 1]) {return false;}}return true;}/*** 查看堆顶元素* @return*/public int peekHeap() {if(data.size() == 0) {throw new NoSuchElementException("heap is empty!");}return data.get(0);}/*** 交换当前数组中 i 和 parent 的值* @param i* @param parent*/private void swap(int i, int parent) {int tmp = data.get(i);int parentVal = data.get(parent);data.set(i,parentVal);data.set(parent,tmp);}/*** 将value存储在堆中* @param value*/public void add(int value) {//1.向数组末尾添加元素this.data.add(value);//2.调整当前堆的结构,使其仍然满足最大堆的性质siftUp(data.size() - 1);}/*** 元素上浮操作* @param i 要上浮的元素索引*/private void siftUp(int i) {while(i > 0 && data.get(i) > data.get(parent(i))) {swap(i,parent(i));//继续向上判断交换后父节点向上的节点关系i = parent(i);}}/*** 取出当前堆的最大值,继续调整堆* @return*/public int extractMax() {//判断当前堆是否为空if(data.size() == 0) {throw new NoSuchElementException("heap is empty!");}int max = data.get(0);//将最后一个元素顶到堆顶int lastElement = data.get(data.size() - 1);data.set(0, lastElement);//删除最后一个元素data.remove(data.size() - 1);//元素下沉siftDown(0);return max;}/*** 元素下沉操作* @param i 要下沉的元素索引*/private void siftDown(int i) {//终止条件:当i还有子树时,说明还没判断结束;若左孩子都不存在,则一定不存在右孩子while(leftChild(i) < data.size()) {//此时i索引对应的元素仍然存在左子树,没到叶子节点int j = leftChild(i);//此时还存在右子树if(j + 1 < data.size() && data.get(j + 1 ) > data.get(j)) {//此时右子树的值大于左子树j = j + 1;}//j一定保存了左右子树的最大值索引if(data.get(i) >= data.get(j)) { //此处为何是 >=//如果此处终止条件是 父节点 > 子节点,也可以,不会死循环//以后在写测试用例时,必须要复杂//此时i对应的元素已经下沉到合适位置break;}else{swap(i,j);i = j;}}}/*** heapify堆化操作:将任意给定的整型数组调整为堆* ①自底向上逐渐调整堆的过程,只看非叶子节点,从最后一个非叶子节点(最后一个非叶子节点就是最后一个节点他爸)开始,一次性砍掉所有叶子节点,进行元素的siftDown操作,直到向上走到根节点即可,时间复杂度为O(n)* ②遍历原数组,依次add操作,时间复杂度为O(nlogn)* @param arr*/public MaxHeap(int[] arr) {//初始化data = new ArrayList<>(arr.length);//1.先将arr的所有元素拷贝到data中for(int i : arr) {data.add(i);}//2.从最后一个非叶子节点开始进行元素下沉for (int i = parent(data.size() - 1); i >= 0 ; i--) {siftDown(i);}}public static void main(String[] args) {
// MaxHeap heap = new MaxHeap();
// heap.add(5);
// heap.add(2);
// heap.add(7);
// heap.add(1);
// heap.add(3);
// System.out.println(heap);
//
// int[] ret = new int[5];
// for (int i = 0; i < ret.length; i++) {
// ret[i] = heap.extractMax();
// }
// System.out.println(Arrays.toString(ret));// int[] data = {17,90,68,12,15,14,70,30,20};
// MaxHeap heap = new MaxHeap(data.length);
// //依次调用extractMax()->集合恰好是一个降序集合
// for (int i = 0; i < data.length; i++) {
// heap.add(data[i]);
// }
// for (int i = 0; i < data.length; i++) {
// data[i] = heap.extractMax();
// }
// System.out.println(Arrays.toString(data));// int[] data = {17,90,68,12,15,14,70,30,20};
// MaxHeap heap = new MaxHeap(data);
// //依次调用extractMax()->集合恰好是一个降序集合
// for (int i = 0; i < data.length; i++) {
// data[i] = heap.extractMax();
// }
// System.out.println(Arrays.toString(data));int n = 10000;int[] data = new int[n];//生成随机数Random random = new Random();for (int i = 0; i < n; i++) {//范围是 0 - Integer.MAX_VALUEdata[i] = random.nextInt(Integer.MAX_VALUE);}MaxHeap heap = new MaxHeap(data);for (int i = 0; i < n; i++) {data[i] = heap.extractMax();}System.out.println(isSorted(data));}
}6.总结
将任意数组调整为堆,而后依次extractMax的操作得到的就是一个排序数组——时间复杂度O(nlogn)。
需要开辟一个和原数组大小完全相同的临时空间——空间复杂度O(n)。
优化:原地堆排序。
