算法打卡day33
今日任务:
1)509. 斐波那契数
2)70. 爬楼梯
3)746.使用最小花费爬楼梯
509. 斐波那契数
题目链接:509. 斐波那契数 - 力扣(LeetCode)
斐波那契数,通常用 F(n) 表示,形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1 给你n ,请计算 F(n) 。示例 1: 输入:2 输出:1 解释:F(2) = F(1) + F(0) = 1 + 0 = 1示例 2: 输入:3 输出:2 解释:F(3) = F(2) + F(1) = 1 + 1 = 2示例 3: 输入:4 输出:3 解释:F(4) = F(3) + F(2) = 2 + 1 = 3提示: 0 <= n <= 30
文章讲解:代码随想录 (programmercarl.com)
视频讲解:手把手带你入门动态规划 | LeetCode:509.斐波那契数哔哩哔哩bilibili
思路:
- 首先定义一个列表
f来存储斐波那契数列的值,初始包含前两项 [0, 1]。- 如果 n 小于等于 1,则直接返回列表中对应位置的值。
- 否则,使用循环从 2 开始遍历到 n,依次计算每一项的值,并添加到列表
f中。- 最后返回列表中索引为 n 的值,即为斐波那契数列的第 n 项
class Solution:def fib(self, n: int) -> int:# 初始化斐波那契数列的前两项f = [0, 1]# 如果 n 小于等于 1,则直接返回对应位置的值if n <= 1:return f[n]# 使用循环计算斐波那契数列的第 n 项for x in range(2, n + 1):# 计算第 x 项的值,并添加到列表中f.append(f[x - 1] + f[x - 2])# 返回斐波那契数列的第 n 项return f[n]这种比较好理解,立马能想到,这里面可以优化的部分在空间复杂度,上面代码空间复杂度O(n)
我们可以定义一个长度为3的列表,反复更新这三个数即可。空间复杂度O(3)
也可以定义3个变量,反复更新3个变量。空间复杂度O(1)
class Solution:# 空间复杂度O(3)def fib(self, n: int) -> int:if n <= 1:return ndp = [0, 1]for i in range(2, n + 1):total = dp[0] + dp[1]dp[0] = dp[1]dp[1] = totalreturn dp[1]# 空间复杂度O(1)def fib(self, n: int) -> int:if n <= 1:return nprev1, prev2 = 0, 1for _ in range(2, n + 1):curr = prev1 + prev2prev1, prev2 = prev2, currreturn prev270. 爬楼梯
题目链接:70. 爬楼梯 - 力扣(LeetCode)
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 注意:给定 n 是一个正整数。示例 1: 输入: 2 输出: 2 解释: 有两种方法可以爬到楼顶。 1 阶 + 1 阶 2 阶示例 2: 输入: 3 输出: 3 解释: 有三种方法可以爬到楼顶。 1 阶 + 1 阶 + 1 阶 1 阶 + 2 阶 2 阶 + 1 阶
文章讲解:代码随想录 (programmercarl.com)
视频讲解:带你学透动态规划-爬楼梯(对应力扣70.爬楼梯)| 动态规划经典入门题目哔哩哔哩bilibili
思路:
爬到第一层楼梯有一种方法,爬到二层楼梯有两种方法。
那么第一层楼梯再跨两步就到第三层 ,第二层楼梯再跨一步就到第三层。
所以到第三层楼梯的状态可以由第二层楼梯 和 到第一层楼梯状态推导出来,那么就可以想到动态规划了。
- 首先定义一个列表
f来存储爬楼梯的方法数,初始包含前三项 [0, 1, 2]。其中 f[0] 为占位符,不参与计算。- 如果 n 小于 3,则直接返回列表中对应位置的值。
- 否则,使用循环从 3 开始遍历到 n,依次计算每一项的值,并添加到列表
f中。每一项的值都等于前两项和前一项的和,因为可以选择爬一阶或者爬两阶台阶。- 最后返回列表中索引为 n 的值,即为爬楼梯的方法数。
class Solution:def climbStairs(self, n: int) -> int:f = [0,1,2]if n < 3:return f[n]for x in range(3,n+1):f.append(f[x-1]+f[x-2])return f[n]# 空间复杂度为O(3)版本def climbStairs(self, n: int) -> int:if n <= 1:return nf = [0] * 3f[1] = 1f[2] = 2for i in range(3, n + 1):total = f[1] + f[2]f[1] = f[2]f[2] = totalreturn f[2]# 空间复杂度为O(1)版本def climbStairs2(self, n: int) -> int:if n <= 1:return nprev1 = 1prev2 = 2for i in range(3, n + 1):total = prev1 + prev2prev1 = prev2prev2 = totalreturn prev2746.使用最小花费爬楼梯
题目链接:746. 使用最小花费爬楼梯 - 力扣(LeetCode)
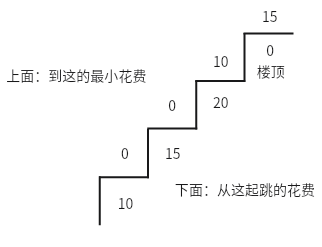
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。 请你找出达到楼层顶部的最低花费。在开始时,你可以选择从下标为 0 或 1 的元素作为初始阶梯。示例 1: 输入:cost = [10, 15, 20] 输出:15 解释:最低花费是从 cost[1] 开始,然后走两步即可到阶梯顶,一共花费 15 。示例 2: 输入:cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] 输出:6 解释:最低花费方式是从 cost[0] 开始,逐个经过那些 1 ,跳过 cost[3] ,一共花费 6 。提示: cost 的长度范围是 [2, 1000]。 cost[i] 将会是一个整型数据,范围为 [0, 999]
文章讲解:代码随想录 (programmercarl.com)
视频讲解:动态规划开更了!| LeetCode:746. 使用最小花费爬楼梯哔哩哔哩bilibili
思路:
用数组展示如下:
class Solution:def minCostClimbingStairs(self, cost: List[int]) -> int:# 如果台阶数小于2,则不需要花费if len(cost) < 2:return 0# 初始化到达前两个台阶的最低花费cost1 = 0cost2 = 0# 将顶部的台阶花费添加到列表中cost.append(0)# print(f'初始化cost1={cost1},cost2={cost2}')# 从第三个台阶开始计算最低花费for i in range(2, len(cost)):# 计算到达当前台阶的最低花费cost_total = min(cost1 + cost[i - 2], cost2 + cost[i - 1])# 更新前两个台阶的最低花费cost1 = cost2cost2 = cost_total# print(f'i={i},cost1={cost1},cost2={cost2},cost_total={cost_total}')# 返回到达顶部的最低花费return cost2