当前位置：首页 > article >正文

Matlab在自动控制领域中的应用

article 2025/8/24 6:43:13

1.1 数学模型

1.1.1建立系统的数学模型

数学是万物的语言。在实际生活中有很多自动控制领域的问题，我们可以对其用数学语言进行描述，即对其建立数学模型。

（1）已知传递函数

假设已经对一个自动控制问题的系统建立了合适的数学模型——传递函数。例如：

$\phi \left ( s \right ) = \frac{25}{s^{2}+6s+ 25}$

那么如何在Matlab中构建它的数学模型呢？

因为传递函数一般都是有理分式，故可以将其拆分为分子和分母，由于分子和分母都是多项有理式，故可以用行向量（也称系数向量）代替多项式（线性代数中的知识）：

（2）已知二阶系统的阻尼比和自然频率

假设我们不知道这个传递函数，只知道它是个标准的二阶系统，其阻尼比为0.6和自然频率为5，我们也可以利用二阶系统的标准形式这样构建分子和分母：

（3）已知开环传递函数，求闭环传递函数

假设没有闭环的传递函数，已知单位负反馈系统下的开环传递函数：

$\phi \left ( s \right ) = \frac{25}{s\left ( s+6 \right ) }$

我们知道

$\phi \left ( s \right ) = \frac{G\left ( s \right ) }{1+G\left ( s \right )H\left ( s \right ) }$

根据这个原理，可以使用Matlab中的feedback()函数构建闭环传递函数，具体操作如下：

（4）已知开环传递函数，求单位反馈的闭环传递函数

如果是单位反馈，则可以用cloop函数构建单位反馈闭环传递函数，单位反馈又分为单位负反馈和单位正反馈：

单位负反馈：

单位正反馈：

(5）已知两个开环传递函数，求串联以后的开环传递函数

现在又有一个惯性环节：其传递函数为：

$G\left ( s \right ) = \frac{1 }{s+1 }$

现在将其与上面的开环传递函数为G(s)的系统进行串联，根据自控所学知识可以知道串联后的整体传递函数为

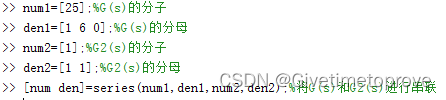
$G\left ( s \right )G_{2} \left ( s \right ) = \frac{25}{s\left ( s+6 \right ) } \cdot \frac{1 }{s+1 }= \frac{25}{s^{3}+7s^{2}+6s }$

可用两种方法，第一种方法是使用series()函数，用法如下：

或者直接使用conv()函数：

可得到结果如下：

总之，得到系统的传递函数的分子num，和分母den，便意味着系统数学模型的成功建立。

（3）带有延迟环节的系统

如果传递函数中含有 $e^{-\tau _{0} t }$ （其中 $\tau _{0}$ 为延迟时常数间），则得到系统具有延时环节，可以将系统拆分成两个子系统串联，一个子系统不带有延迟环节，另一个子系统带有延迟环节。并且可以通过数学方法用n阶有理函数（有理分式）近似代替延迟环节的传递函数，如带有延迟环节的子系统传递函数为：

$G_{2}(s)=e^{-0.5t}$

建立3阶有利函数近似模型为：

1.1.2建立传递函数对象

(1)已知传递函数的分子num，和分母den

已知分子、分母多项式后可利用tf()函数可建立传递函数对象：

工作区中可以得到如下对象：

（2）已知传递函数的零点、极点和根轨迹增益

除此之外，还可以用zpk()函数建立传递函数对象，例如已经知道一个传递函数无零点，极点为0和-6，根轨迹增益为25，则可用zpk()函数建立数学模型：

至此，一个系统的数学模型和传递函数对象便建立好了。

1.2时域分析

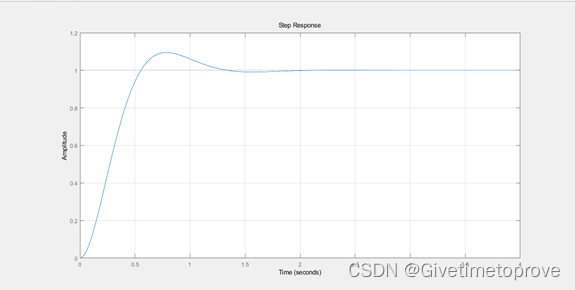
1.2.1求取单位阶跃响应或者单位脉冲响应

1、给定时间

由于是时域分析，故先给定一个时间范围；

2、求单位脉冲或阶跃响应

或者

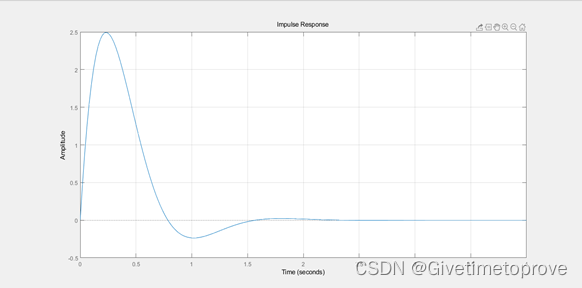
图单位脉冲响应

或者

图单位阶跃响应

注意：这里用的step()函数和impulse()函数也可以不输入时间t变量，t在sys的时间单位属性中是指定的，另外输入参数可以是分子分母形式（num、den），也可以是传递函数对象（sys）形式（后面的函数若输入参数都可使用这两种形式，则统一使用传递函数对象形式）。

3、求其他响应

对于不是单位脉冲、阶跃的响应可以利用lsim()函数求取，例如单位斜坡函数：u(t)=t

1.2.2判定稳定性

我们知道，通过一个闭环系统的极点（即系统特征方程的根），可以帮助我们判断系统的稳定性能。还是利用这一传递函数：

$\phi \left ( s \right ) = \frac{25}{s^{2}+6s+ 25}$

可知其特征方程为 $s^{2}+6s+25=0$ ，用Matlab构造系统特征方程并判断稳定性如下操作：

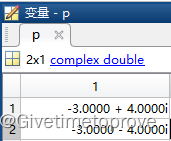
得根的结果如下：

均位于s平面的左半平面，故此系统是稳定的。若遇到其他情况，请根据所学知识自行判断稳定性。

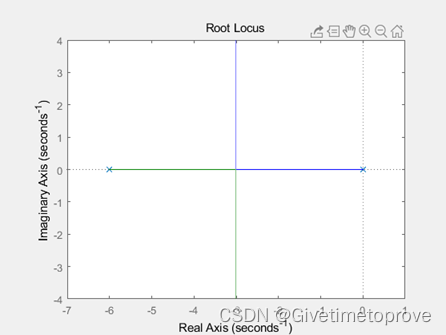
1.3 根轨迹

对于二阶系统的开环传递函数：

$\phi \left ( s \right ) = \frac{25}{s\left ( s+6 \right ) }$

绘制根轨迹的代码和结果如下：

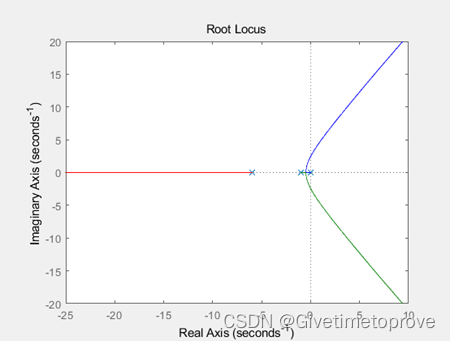
对于开环传递函数为

$G\left ( s \right )G_{2} \left ( s \right ) = \frac{25}{s\left ( s+6 \right ) } \cdot \frac{1 }{s+1 }= \frac{25}{s^{3}+7s^{2}+6s }$

的三阶系统绘制根轨迹的结果如下：

1.4频域分析

在频域分析中，一般有三个重要图像，分别是奈式曲线，波特图，和对数幅频渐进特性曲线。

（一）奈式曲线

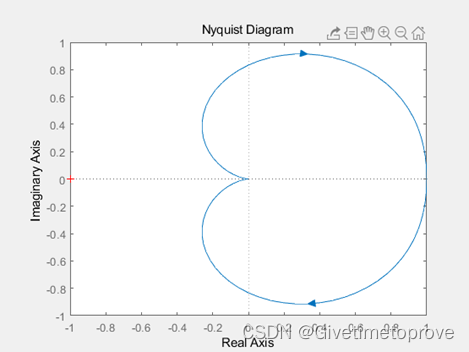
针对传递函数为：

$\phi (s)=\frac{25}{s^{2}+6s+25}$

若求奈式曲线，可以用nyquist()函数，代码如下：

结果如下：

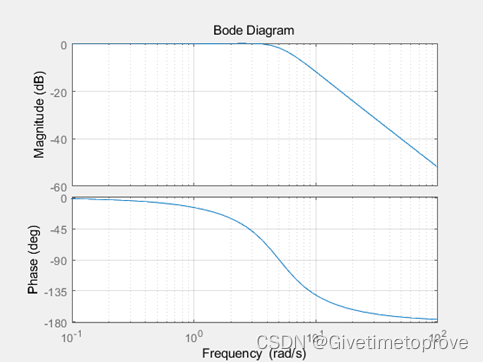
若求波特图，可以使用bode()函数或者margin()函数，使用bode()函数代码如下：

结果如下：

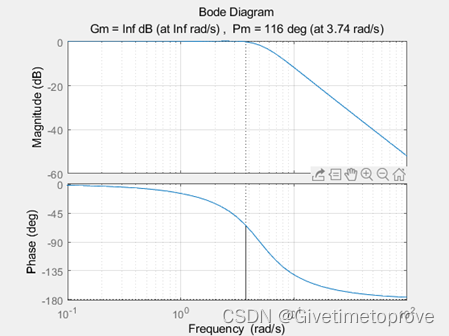
使用margin()函数代码如下：

结果如下：

唯一不同之处在于margin()可在图像上显示截止频率，穿越频率，相角裕度和幅值裕度，如果使用参数来传递这些数值，则不会显示图像如下图：

若求对数幅频渐进特性曲线，需要用到自定义函数名为bd_asymp()，数的内部代码如下（这里的代码参考胡寿松老先生的《自动控制原理》）：

function[wpos,ypos]=bd_asymp(G,w)G1=zpk(G);wpos=[];pos1=[];if nargin==1,w=freqint2(G);endzer=G1.z{1}; pol=G1.p{1};gain=G1.k;for i=1:length(zer);if isreal(zer(i))wpos=[wpos,abs(zer(i))];pos1=[pos1,20];elseif imag(zer(i))>0wpos=[wpos,abs(zer(i))];pos1=[pos1,40];endendendfor i=1:length(pol);if isreal(pol(i))wpos=[wpos,abs(pol(i))];pos1=[pos1,-20];elseif imag(pol(i))>0wpos=[wpos,abs(pol(i))];pos1=[pos1,-40];endendendwpos=[wpos w(1) w(length(w))];pos1=[pos1,0,0];[wpos,ii]=sort(wpos);pos1=pos1(ii);ii=find(abs(wpos)<eps);kslp=0;w_start=1000*eps;if length(ii)>0kslp=sum(pos1(ii));ii=(ii(length(ii))+1):length(wpos);wpos=wpos(ii);pos1=pos1(ii);endwhile 1[ypos1,pp]=bode(G,w_start);if isinf(ypos1),w_start=w_start*10;else break;endendwpos=[w_start wpos];ypos(1)=20*log10(ypos1);pos1=[kslp pos1];for i=2:length(wpos)kslp=sum(pos1(1:i-1));ypos(i)=ypos(i-1)+kslp*log10(wpos(i)/wpos(i-1));endii=find(wpos>=w(1)&wpos<=w(length(w)));wpos=wpos(ii);ypos=ypos(ii);

Matlab中可以使用bd_asymp函数后，代码如下：