公开密钥加密算法RSA的理论概述
目录
1.RSA公钥密码体制
2.RSA公钥密码算法步骤
3.RSA公钥密码算法的算法流程图
3.1 生成密钥对
3.2 加密
3.3解密
RSA加密算法的最大优点就是不需要对密钥通信进行保密,所需传输的只有公开密钥,这样就省去了一条开销很大的密钥传输信道。其保密性强,密钥管理方便,并且具有数字签名、认证和签别等多种功能,特别适合于现代保密通信的需要。大多数使用公钥密码进行加密和数字签名的产品和标准使用的都是RSA算法。RSA的安全性是基于大数因子分解的困难性。目前一般认为RSA需要1024位以上的字长才有安全保障。由于RSA所采用的模幂运算耗时太多,因此它通常只能用于加密少量数据或者加密密钥。需要注意的是,RSA的安全性只是一种计算安全性,绝对不是无条件的安全性,这是由它的理论基础决定的。所以,在实现RSA算法的过程中,每一步都应该尽量从安全性方面考虑。
1.RSA公钥密码体制
公钥加密算法的典型代表是RSA (Rivest , Shamir , Adelman)算法 ,它是公共密钥机制中的一种比较成熟的算法。它是建立在“大数分解和素数据检测”的理论基础上的,两个大素数相乘在计算机上是容易实现的, 但将该乘积分解成两个素数因子的计算量却相当巨大, 大到甚至在计算机上不可能实现,所以就确保了RSA算法的安全性。RSA算法是第一个既能用于数据加密又能用于数字签名的算法, 它为公用网络上信息的加密和鉴别提供了一种基本的方法。
2.RSA公钥密码算法步骤
首先,产生密钥
(1)随机选取两个大素数p与q;
(2)计算n=p*q(公开),Φ(n)=(p-1)*(q-1)(保密);
(3)随机选取正整数e,使之满足gcd(e,Φ(n))=1,且1<e<Φ(n);
(4)利用欧几里得算法计算d,使之满足ed≡1(modΦ(n)),d为保密的解密密钥;
(5)用E=<n,e>作为公钥,用D=<n,d)>作为私钥。
其次,加密和解密,用RSA公钥密码体制加密时,先将明文数字化,然后进行分组,每组的长度不超过log(n),再每组单独加密和解密。
RSA算法主要的参数有3 个:模数n 、加密密钥e和解密密钥d 。
RSA算法的核心参数确实包括以下三个:
-
模数n: 模数是RSA算法中的一个非常大的整数,通常由两个大素数p和q相乘得到,即n=p×q。模数的大小直接影响了RSA算法的安全性,因为攻击者如果想要破解RSA加密就必须有效地对n 进行因数分解,而这在目前对于足够大的n 来说,是非常困难的。
-
加密密钥e: 也称为公钥指数,是一个相对较小的标准整数,通常选择为65537或者其它与ϕ(n) 互质的数(其中ϕ(n)=(p−1)(q−1) 是欧拉函数的值,表示小于并与n 互质的正整数的数量)。e 必须是与ϕ(n) 互质的,这样在加密过程中才能确保存在对应的解密密钥。
-
解密密钥d: 解密密钥是加密密钥e 的一个逆元,满足d⋅e≡1modϕ(n)。这个关系可以通过扩展欧几里得算法找到。只有知道d 的人才能成功地对用公钥(n,e) 加密的消息进行解密,从而保护了信息安全。
在RSA体系中,公钥是包含(n,e) 的一对,可以公开分发;而私钥则是(n,d),必须保密保管。通过这样的设计,实现了非对称加密,即加密和解密使用不同的密钥,并且加密密钥不能轻易推导出解密密钥。
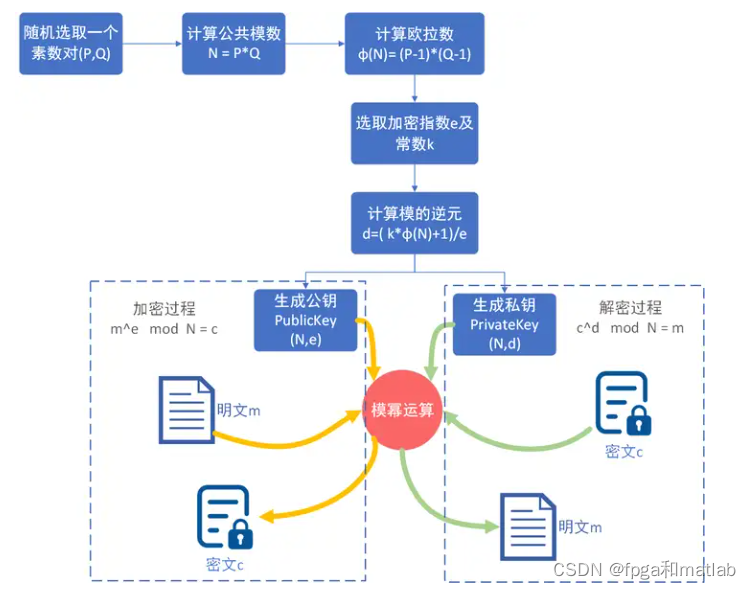
3.RSA公钥密码算法的算法流程图
RSA公钥密码算法是一种非对称加密算法,它的特点是拥有两个密钥:公钥和私钥,公钥用于加密,私钥用于解密,任何人都可以获取公钥进行加密,但只有拥有私钥的人才能解密。以下是RSA算法生成密钥、加密和解密的详细过程:
3.1 生成密钥对
-
选择两个大素数p 和q。这两个素数应该足够大以保证安全性,且尽量随机选择以增加因数分解的难度。
-
计算模数n:将两个素数相乘得到模数n=p×q。
-
计算欧拉函数 φ(n):ϕ(n)=(p−1)(q−1)。欧拉函数φ(n)表示在小于n并且与n互质的正整数的数量。
-
选择加密指数e:选择一个与ϕ(n) 互质的奇数e,且1<e<ϕ(n)。通常会选择一个较小的固定值如e=65537,以提高计算效率。
-
计算解密指数d:找到一个整数d 使得e×d≡1modϕ(n),也就是说ed≡1modϕ(n)。这可以通过扩展欧几里得算法来求解。
于是,公钥为 (n, e),私钥为 (n, d)。
其流程图如下图所示:

3.2 加密
给定明文M(转换为整数),使用接收者的公钥(n,e) 加密:
转换明文:将明文信息转换为一个整数M,确保M<n。
加密计算:利用加密指数e 和模数n 对明文进行幂运算,得到密文C:
其流程图如下图所示:

3.3解密
持有私钥(n,d) 的接收者收到密文C 后,进行解密:
解密计算:利用解密指数d 和模数n 对密文进行幂运算,还原明文M:
M=Cdmodn
由于ed≡1modϕ(n),因此Cdmodn 等价于(Me)dmodn,经过模反元素的性质化简后可以恢复原来的明文 M。
其流程图如下图所示:

