Verilog曼彻斯特编解码器设计
目录
第1章 项目背景... 1
1.1 编码技术的发展... 1
1.1.1 NRZ码... 1
1.1.2 RZ编码... 1
1.1.3 传号差分编码... 1
1.1.4 曼彻斯特编码... 1
第2章 设计方案... 3
2.1 设计任务... 3
2.2 设计指标... 3
2.3 设计方案... 3
2.3.1 RZ码的实现... 4
2.3.2 传号差分码的实现... 4
2.3.3 曼彻斯特码的实现... 5
2.3.4 数据的采样与恢复... 5
2.4 实验仿真... 6
2.4.1 基础部分仿真... 6
2.4.2 扩展部分仿真... 7
第1章 项目背景
1.1 编码技术的发展
数字编码技术在以太网中的发展历程可以追溯到20世纪70年代。当时,以太网作为一种局域网标准,使用模拟信号传输数据。随着计算机技术的不断发展,对数据传输速率的要求也越来越高。为了提高传输速率,人们开始研究数字编码技术。数字编码技术可以将模拟信号转换为数字信号,从而提高了传输速率和可靠性。随着以太网技术的不断发展,数字编码技术也不断得到改进和完善。目前,以太网已经成为了世界上最流行的局域网标准之一,数字编码技术也成为了以太网中不可或缺的一部分。
1.1.1 NRZ码
NRZ码,也叫不归零编码,是我们最常见的一种编码,即正电平表示1,低电平表示0。它与RZ码的区别就是它不用归零,也就是说,一个周期可以全部用来传输数据,这样传输的带宽就可以完全利用。一般常见的带有时钟线的传输协议都是使用NRZ编码或者差分的NRZ编码。
1.1.2 RZ编码
RZ码,是归零编码的一种编码方式。在RZ编码中,正电平代表逻辑1,负电平代表逻辑0,并且每传输完一位数据,信号返回到零电平。它与NRZ码的区别主要在于编码方式:RZ码将数字信号分为两个等长的部分,在一个时钟周期中,信号的值在一个部分中为高电平,在另一个部分中为低电平。
1.1.3 传号差分编码
传号差分编码是一种数字编码方式,它利用相邻码元波形(或电平)是否跳变来传递信息,与码元本身电平或极性无关。在传号差分编码中,每个数字都是前一个数字的差值,这种编码方式可以用于数据压缩、数据传输和数据存储等领域。传号差分编码的优点在于它可以减少数据传输的带宽和存储空间。因为在传输或存储数据时,只需要传输或存储差分序列,而不是每个数字的绝对值。这可以大大减少数据传输和存储的开销。此外,传号差分编码还具有抗干扰性能强的优点。即使在存在干扰的情况下,只要干扰不会改变差分序列的相对值,就可以在一定程度上抵抗干扰。
1.1.4 曼彻斯特编码
曼彻斯特编码也是一种常见的线码方式,用于数字数据的传输。其基本原理是将数据位拆分成两个相等的时段,每个时段内都有信号变化,0表示高-低电平过渡,1表示低-高电平过渡。非归零曼彻斯特编码在每个位周期内都有信号变化,时钟恢复容易,而归零曼彻斯特编码引入零插入机制,提供额外电平变化,适用于要求更强的时钟同步和可靠传输的应用。这种编码方式常用于以太网等通信协议,确保数据的可靠传输和时钟同步。
第2章 设计方案
2.1 设计任务
(1)基本设计:采用状态机结合组合逻辑结构设计串行数据编码器,输入为NRZ码,要求实现把输入码转换为转换为RZ码,传号差分码,曼彻斯特码(10,01)功能,串行码数据速率为9600bit/s,要求数据无拥塞,最大延时为两个码元,空闲时信号为高电平,起始码为1bit低电平。
(2)扩展设计:数据9600bit/s从串口来,采用1MHz超采样,实现数据9600bit/s NRZ码恢复,然后进行码变换。
2.2 设计指标
(1)串行码数据速率为9600bit/s
(2)要求数据无拥塞,最大延时为两个码元
(3)空闲时信号为高电平,起始码为1bit低电平
(4)采用1MHz超采样,实现数据9600bit/s NRZ码恢复
2.3 设计方案
为完成该课程设计,需要设计一个可行、高效的设计方案。
在设计时应该包含一个系统的总时钟clkin,需要被编码的输入数据NRZ码datain_nrz,输出数据RZ码dataout_rz,传号差分码dataout_dif以及曼彻斯特码dataout_mc,考虑到RZ码和曼彻斯特码的数据频率应是原始数据频率的2倍。传号差分码的数据频率应是系统时钟频率的2倍,所以需要一个分频器,把系统的时钟频率进行二分频,方便RZ码的使用。总体的设计思路是:输入随机的NRZ码,利用相应的编码规则,输出编码后的RZ码、传号差分码和曼彻斯特码。
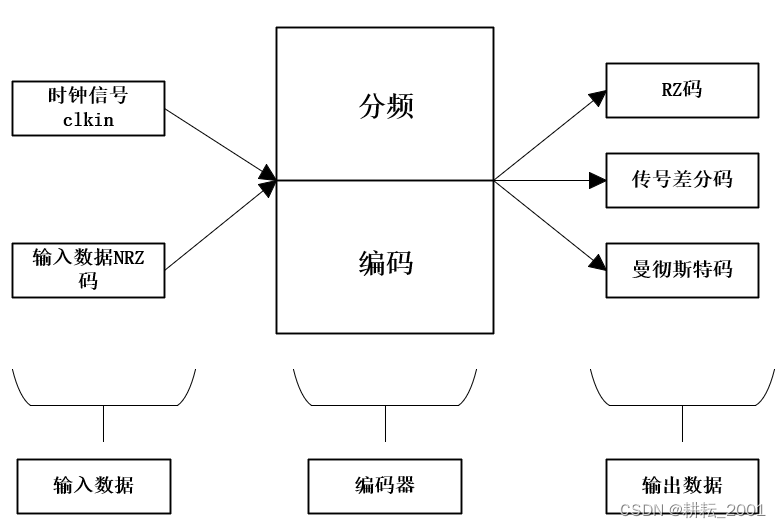
图2-1 基础部分设计方案
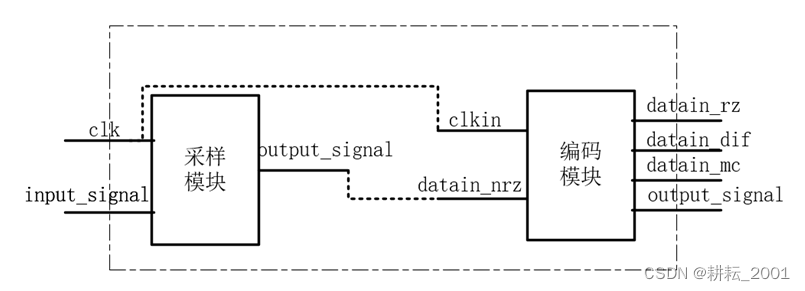
图2-2 扩展部分设计方案
2.3.1 RZ码的实现
例如输入的NRZ码是0110,根据RZ码的编码规则,在一个数据周期内,NRZ码的0会被编码成RZ码的00,NRZ码的1会被编码成RZ码的10,那么最后的答案应该是0010 1000,需要注意的是,这时RZ码的频率是NRZ码的2倍。
如图2-3所示,输入的随机数据前8位是0110 1001,那么对应的RZ编码结果是0010 1000 1000 0010。编码结果完全正确。
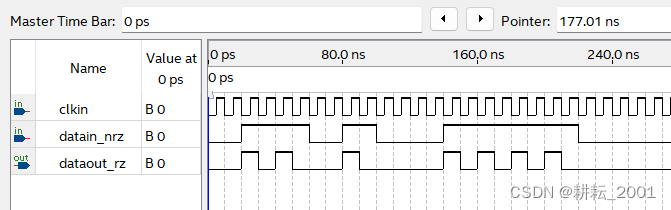
图2-3 RZ编码时序仿真
2.3.2 传号差分码的实现
根据传号差分码的编码规则,传号差分码是比较输入的NRZ码的当前位的数据与前一位数据是否相同,也就是是否发生了跳变,若有跳变则传号差分码的值为1,否则为0;那么在实现的过程中NRZ码的第一位应该与传号差分码的第一位数据相同。但是我在思考如何实现编码的时候,突然意识到,传号差分码的编码规则其实是输入数据当前位和前一位进行异或操作,那么问题也变的简单起来。
在实现时,只需要把传进来的数据先暂存,让它与下一次收到的数据进行异或操作,并把异或值输出即可。例如输入的NRZ码还是0110,传号差分码保持第一个数据不变,从第二位开始,当前位和前一位进行异或操作并输出异或值。所以输出的传号差分码应该是0101。另外,传号差分码的频率和输入的NRZ码的频率一样。
如图2-4所示,当输入随机数据的前8位为1010 0110时,输出的传号差分编码结果为1111 0101。编码结果也是完全正确的。这里需要说明的是输出波形图延迟了时钟信号clkin的半个周期。
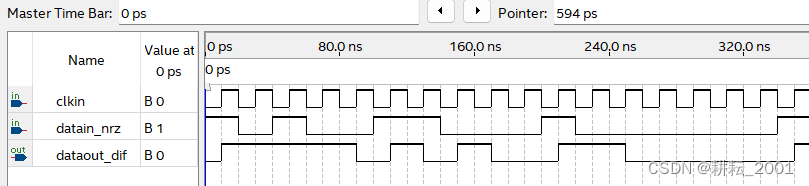
图2-4 传号差分编码时序仿真
2.3.3 曼彻斯特码的实现
曼彻斯特编码与RZ编码的编码规则有很大的相似性,编码后数据的频率是原始数据频率的2倍。曼彻斯特编码实际上是让原始数据产生一个跳变,例如让原始数据的0编码成01,让原始数据的1编码成10。所以,如输入数据为NRZ码0110,那么经过曼彻斯特编码后的结果是0110 1001。
如图2-5仿真结果所示,输入随机数据的前8位是0100 0011,对应的曼彻斯特编码的结果为0110 0101 0101 1010。编码结果完全正确。

图2-5 曼彻斯特编码时序仿真
2.3.4 数据的采样与恢复
题目要求要对从串口来的数据9600bit/s,采用1MHz超采样,实现数据9600bit/s NRZ码恢复。所以需要在一个数据周期进行1000000/9600≈104次采样。
如图2-6所示,输入数据input_signal的前8位数据为0110 1000,经采样后恢复的数据output_signal延迟了一个原始数据周期,所以忽略前一个数据,从而得到恢复的数据依旧是0110 1000。
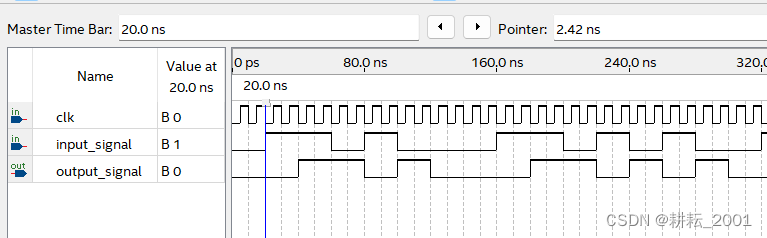
图2-6 数据采样与恢复时序仿真
2.4 实验仿真
2.4.1 基础部分仿真
实现了各自单独的数据编码后,需要把三种编码器的代码进行合并,以满足该课程设计的内容要求。最终仿真结果如图2-7所示。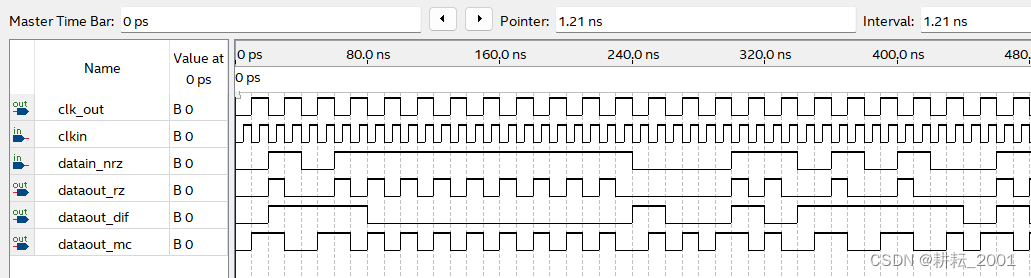
图2-7 基础部分时序仿真
图中clkin表示系统的总时钟信号,clk_out表示进行二分频后的时钟信号,dataout_nrz、dataout_rz、dataout_dif、dataout_mc分别表示输入数据NRZ码、输出数据RZ码、传号差分码以及曼彻斯特码。可以看到NRZ码的前8位数据为0101 1111,经过编码后的RZ码为0010 0010 1010 1010,传号差分码为0111 0000,曼彻斯特码为0110 0110 1010 1010,仿真结果完全正确。另外,由仿真结果也可以看出传号差分码的频率与原始数据NRZ码频率相同,RZ码和曼彻斯特码的频率是原始数据NRZ码的2倍。
2.4.2 扩展部分仿真
在进行数据采样并恢复出原始数据后,把恢复的数据再进行编码。如图2-8所示,输入被采样数据是input_signal,恢复得到的数据是output_signal,可以发现,output_signal有一定的延迟,忽略延迟的数据,后面的数据和input_signal数据相同;另外由于数据的延迟,导致编码后的数据也有相应的延迟,但是可以看出,当忽略延迟的数据时,对数据的编码完全正确。
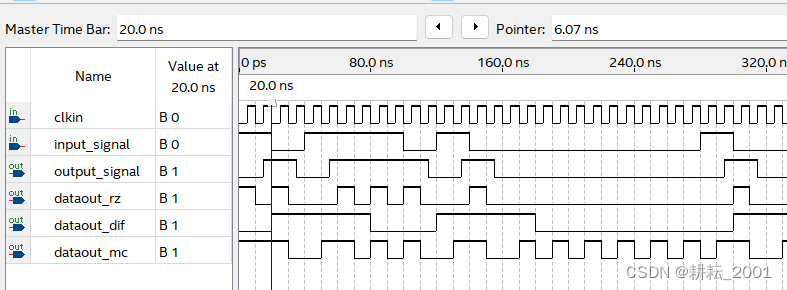
图2-8 扩展部分时序仿真
图中output_signal的前8位数据是1011 1010,编码后的数据是从图中蓝色竖线后面开始的,即编码后的RZ码为1000 1010 1000 1000,传号差分码为1110 0111,曼彻斯特码为1001 1010 1001 1001。可见,对采样后恢复的数据进行编码也完全正确。
2.5 代码
1. module bianma(
2. input clkin,
3. input datain,
4. output dataout_rz,
5. output dataout_mc,
6. output reg clk_out,
7. output reg dataout_dif
8. );
9.
10. always @(negedge clkin) begin
11. clk_out <= ~clk_out;
12. end
13.
14. reg [1:0] tmp_rz;
15. reg flag_rz = 1;
16. always @(negedge clkin) begin
17. if (flag_rz == 1 || flag_rz == 0) begin
18. if (datain == 1'b0)
19. tmp_rz <= 2'b00;
20. else
21. tmp_rz <= 2'b10;
22. end
23. end
24. always @(negedge clkin) begin
25. flag_rz <= ~flag_rz;
26. end
27. assign dataout_rz = (flag_rz == 0) ? tmp_rz[0] : tmp_rz[1];
28.
29. reg [1:0] tmp_mc;
30. reg flag_mc = 1;
31. always @(negedge clkin) begin
32. if (flag_mc == 1 || flag_mc == 0) begin
33. if (datain == 1'b0)
34. tmp_mc <= 2'b01;
35. else
36. tmp_mc <= 2'b10;
37. end
38. end
39. always @(negedge clkin) begin
40. flag_mc <= ~flag_mc;
41. end
42. assign dataout_mc = (flag_mc == 0) ? tmp_mc[0] : tmp_mc[1];
43.
44. reg prev_bit;
45. always @(negedge clk_out) begin
46. if (prev_bit == datain) begin
47. dataout_dif <= 1'b0;
48. end else begin
49. dataout_dif <= 1'b1;
50. end
51. prev_bit <= datain;
52. end
53.
54. endmodule1. module manchester(
2. input clk, // 时钟信号
3. input input_signal, // 采样信号
4. output dataout_rz,
5. output dataout_mc,
6. output wire clk_out,
7. output wire dataout_dif
8. );
9. wire date;
10.
11. caiyang u1(
12. .clk(clk),
13. .input_signal(input_signal),
14. .output_signal(data)
15. );
16.
17.
18. bianma u2(
19. .clkin(clk),
20. .datain_nrz(data),
21.
22. .dataout_rz(dataout_rz),
23. .dataout_mc(dataout_mc),
24. .clk_out(clk_out),
25. .dataout_dif(dataout_dif)
26. );
27. endmodule 1. module caiyang(
2. input clk, // 时钟信号
3. input input_signal, // 采样信号
4. output reg output_signal // 输出信号
5. );
6.
7. reg sample_value; // 采样值
8.
9. always @(negedge clk) begin
10. sample_value <= input_signal;
11. if (sample_value) begin
12. output_signal <= 1'b1;
13. end else begin
14. output_signal <= 1'b0;
15. end
16. end
17.
18. endmodule
