注意力机制总结
文章目录
- 1. 通道注意力
- 1.1 SENet(谁用谁知道,用了都说好)
- 2. 通道&空间
- 2.1 CBAM
- 2.2 scSE
- 2.3 Coordinate Attention
- 3. self-attention
- 3.1 Non-local
- 3.2 CCNet
- 3.3 DANet
- 4. Branch Attention
- 4.1.SKNet
- 参考资料
1. 通道注意力
1.1 SENet(谁用谁知道,用了都说好)
论文:Squeeze-and-Excitation Networks
- SE模块

- 具体实现
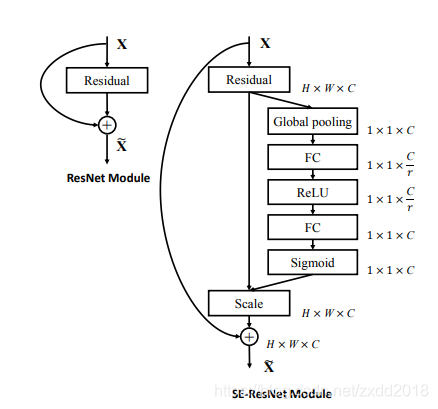
- 解释:对于尺寸为H×W×C的特征图,首先通过全局平均池化对每个feature map进行压缩,得到1×1×C的向量,这一步骤称作Squeeze;然后引入两个全连接层进行Excitation,通过sigmoid将其归一化到0~1之间,即每个通道的权重;最后通过将权重与原始输入对位相乘,实现通道的重标定。
- 为什么使用两个全连接层:限制模型复杂度,增加泛化性
2. 通道&空间
2.1 CBAM
论文:CBAM: Convolutional Block Attention Module
串联的通道注意力加空间注意力
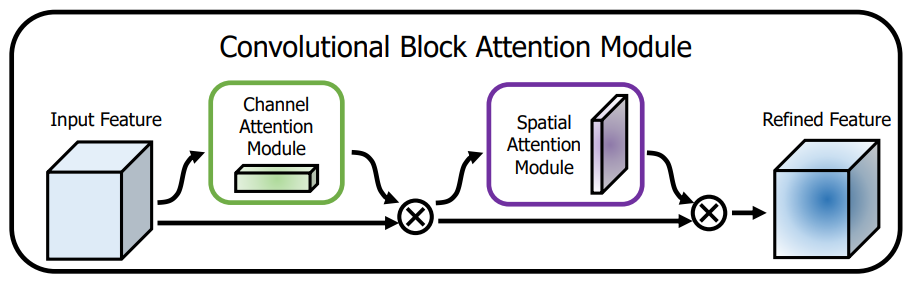
通道注意力使用了maxpool和avgpool压缩空间维度,空间注意力使用了maxpool和avgpool压缩通道维度
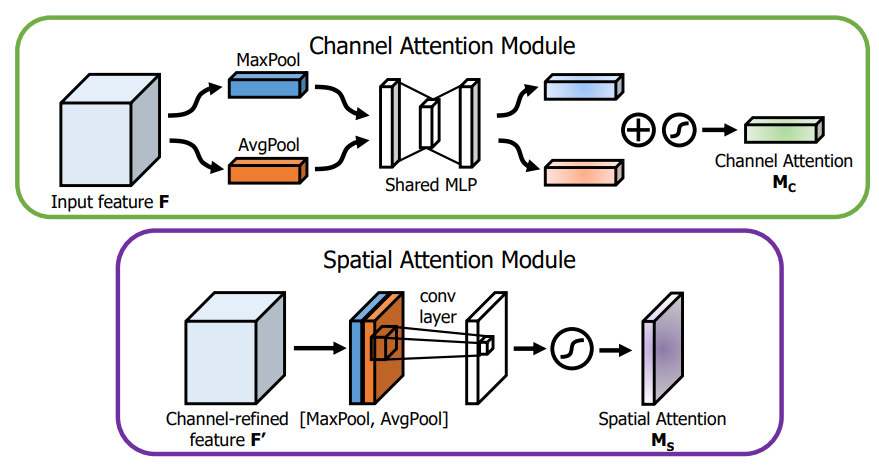
2.2 scSE
论文:Concurrent Spatial and Channel ‘Squeeze & Excitation’ in Fully Convolutional Networks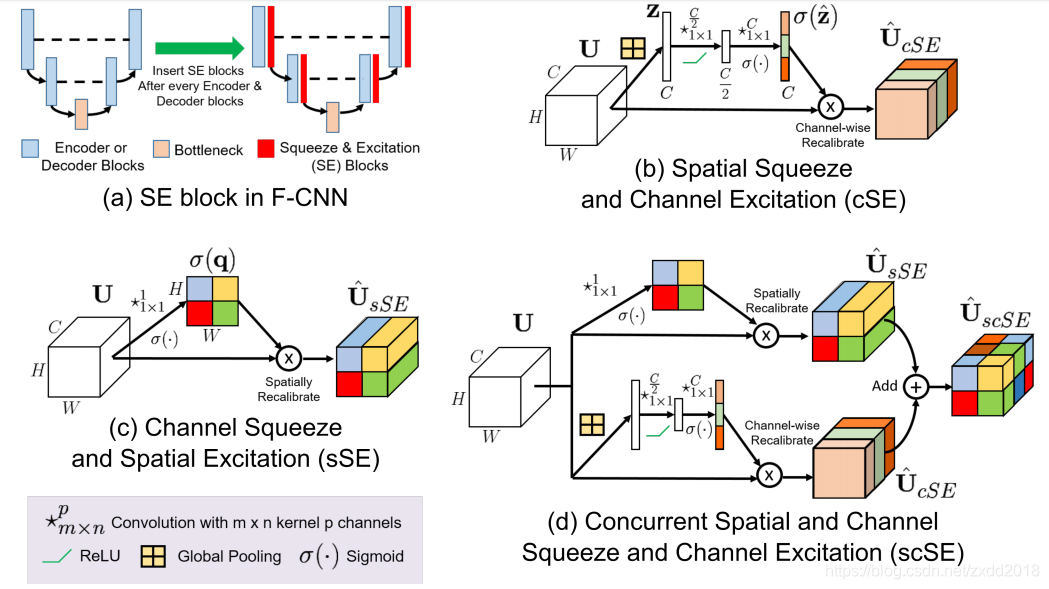
- cSE:与SENet本质相同,区别在于升降维度的超参数 r 取值为2或16,兼顾模型的复杂度和准确率
- sSE:从空间角度引入注意力机制。将尺寸为H×W×C的特征图经过1×1卷积降维,得到H×W×1的特征图。然后再经过特征重标定,与原来的U对应空间上相乘得到U^。
- scSE:从通道和空间两个角度同时引入注意力机制,相当于cSENet和sSENet的结合。
2.3 Coordinate Attention
论文:Coordinate Attention for Efficient Mobile Network Design
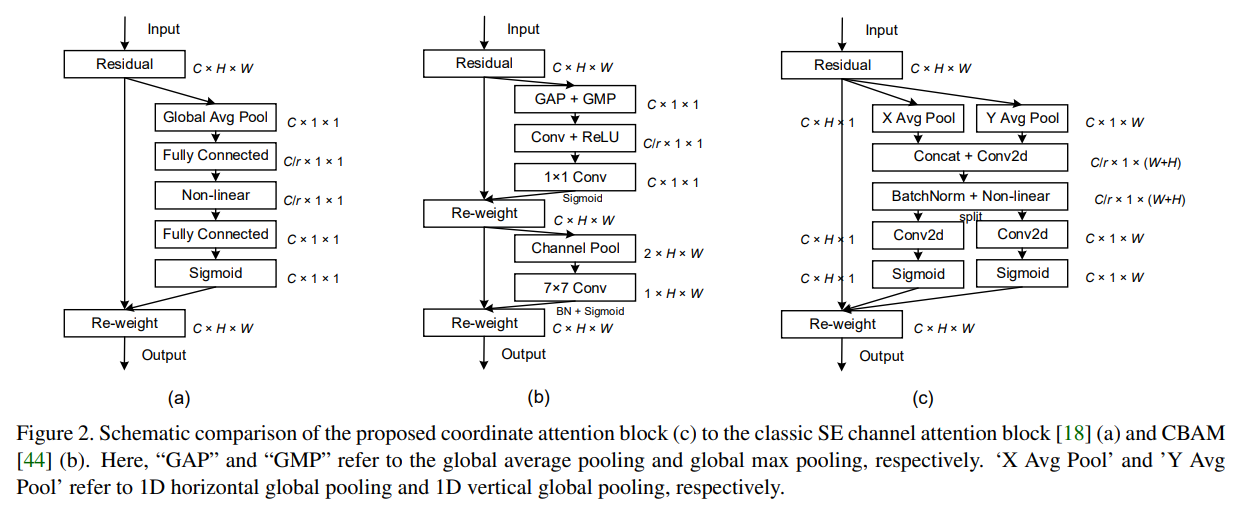
3. self-attention
3.1 Non-local
论文:Non-local Neural Networks

3.2 CCNet
论文:CCNet: Criss-Cross Attention for Semantic Segmentation
针对non-local计算复杂度高的问题进行改进

单独使用只能建模十字位置的依赖关系,循环两次即可建模任意位置的依赖关系

3.3 DANet
论文:Dual Attention Network for Scene Segmentation
考虑到non-local只建模了空间位置的长期依赖,没有考虑到通道间的依赖关系,提出了双重注意力融合网络,整体结构如下:

位置注意力模块和通道注意力模块的结构

4. Branch Attention
4.1.SKNet
论文:Selective Kernel Networks
- Motivation:我们在看不同尺寸不同远近的物体时,视觉皮层神经元接受域大小是会根据刺激来进行调节的。那么对应于CNN网络,一般来说对于特定任务特定模型,卷积核大小是确定的,那么是否可以构建一种模型,使网络可以根据输入信息的多个尺度自适应的调节接受域大小呢?
- SK Block
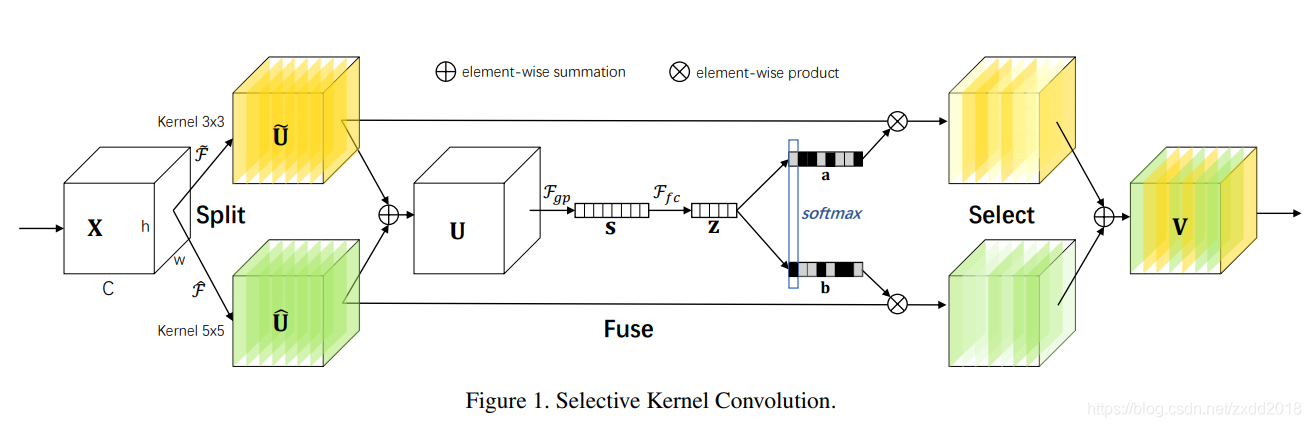
- SK Block分为三个步骤:
1.Split:特征图 X ∈ R H ′ × W ′ × C ′ X\in \mathbb{R}^{H^{\prime}\times W^{\prime}\times C^{\prime}} X∈RH′×W′×C′分别通过3×3卷积和5×5卷积得到 U ~ ∈ R H × W × C \widetilde{U}\in \mathbb{R}^{H\times W\times C} U ∈RH×W×C和 U ^ ∈ R H × W × C \hat{U}\in \mathbb{R}^{H\times W\times C} U^∈RH×W×C;
2.Fuse:对 U ~ \widetilde{U} U 和 U ^ \hat{U} U^执行add操作得到 U ∈ R H × W × C U\in \mathbb{R}^{H\times W\times C} U∈RH×W×C,然后经过全局平均池化得到 S ∈ R C S\in \mathbb{R}^C S∈RC,再经过全连接层得到 Z ∈ R d Z\in \mathbb{R}^d Z∈Rd。接下来是重点, Z Z Z分别经过两个全连接层(对应论文中的 A ∈ R C × d A\in \mathbb{R}^{C\times d} A∈RC×d和 B ∈ R C × d B\in \mathbb{R}^{C\times d} B∈RC×d)得到 a ∈ R C a\in \mathbb{R}^{C} a∈RC和 b ∈ R C b\in \mathbb{R}^{C} b∈RC,再对 a a a和 b b b在行的维度上做softmax即可得到 U ~ \widetilde{U} U 和 U ^ \hat{U} U^的通道权重;
3.Select:由于 a + b = 1 a+b=1 a+b=1,通过赋予 U ~ \widetilde{U} U 和 U ^ \hat{U} U^通道不同权重实现对不同kernel的”自适应选择“。
参考资料
https://github.com/MenghaoGuo/Awesome-Vision-Attentions
