3D-Lidar点云数据处理

3D-Lidar点云数据处理

本篇博客，记录自己学习处理3D-Lidar点云数据目前遇到的算法及本工程使用的算法，作为记录有不足的地方，烦请大家批评指正、指导。

原始激光点云数据滤波

参考Being_young大佬文章：https://blog.csdn.net/u013019296/article/details/70052319

对于原始点的滤波，觉得目前PCL库已经做了很好的处理，PCL库中给出几种需要进行点云滤波处理情况：

1. 点云数据密度不规则需要平滑；
2. 扫描时，由于障碍物可能会存在遮挡，离群点需要去除；
3. 数据太大需要下采样（现在已经遇到这个数据量太大的问题了，16线的Lidar一次采样存在 ( 32 + 16 * 2 ) * 360 / 0.18 = 128000 个点云数据）；
4. 去除噪声

对应解决方案：

1. 给定的规则限制过滤去除点
2. 通过常用滤波算法修改点的部分属性，统计滤波
3. 下采样（测试选在0.1，过滤可达到50%以上）

PCL库直通滤波例子

pcl::PointCloud<pcl::PointXYZ>::Ptr cloud (new pcl::PointCloud<pcl::PointXYZ>);
pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_filtered (new pcl::PointCloud<pcl::PointXYZ>);
/**
* 1、创建直通滤波器的对象，设立参数，滤波字段名被设置为Z轴方向
* 2、通过函数setFilterLimitsNegative，过滤所有点的Z轴坐标不在该范围内的点过滤掉（false）或保留（true） 
*/
// 设置滤波器对象
pcl::PassThrough<pcl::PointXYZ> pass；	// 声明滤波器对象
pass.setInputCloud (cloud);				// 设置输入点云(ptr指针)
pass.setFilterFieldName ("z");			// 设置过滤x,y,z哪个方向
pass.setFilterLimits (-1.8, 0.5);		// 设置在过滤方向的范围
pass.setFilterLimitsNegative (false);   // 设置保留范围内还是过滤掉范围内
pass.filter (*cloud_filtered);			// 执行滤波，保存过滤结果到cloud_filtered(ptr指针)

PCL库体素下采样例子

本工程使用的滤波器

/**
* 创建pcl::VoxelGrid滤波器对象，并设置叶素大小为1cm
*/
pcl::VoxelGrid<pcl::PCLPointCloud2> vg;	// 创建滤波对象
vg.setInputCloud (cloud);				// 输入点云（ptr指针）
vg.setLeafSize (0.01f, 0.01f, 0.01f);	// 设置体素体积为1cm的立方体
vg.filter (*cloud_filtered);			// 执行滤波处理，存储输出

PCL库统计滤波器例子

/**
* 1、创建统计滤波器statisticalOutlierRemoval对象
* 2、设置在进行统计时考虑查询点临近点数
*/
pcl::StatisticalOutlierRemoval<pcl::PointXYZ> sor;	// 创建滤波器对象  
sor.setInputCloud(cloud);							// 输入点云（ptr指针）
sor.setMeanK(50);									// 设置在进行统计时考虑查询点临近点数  
sor.setStddevMulThresh(1.0);						// 设置判断是否为离群点的阀值  
sor.filter(*cloud_filtered);						// 执行滤波处理，存储输出  

点云分割（地面与非地面）

1. Fast Segmentation of 3D Ponit Clouds for Ground Vehicles 论文实现 文章解读 IEEE 文章下载
2. PCL库，随机采样一致性实现

本工程采用快速分割
1、根据Lidar旋转角度和角分辨率分割扇形区域，sector_num = 360° / 0.18°；0.18是水平角分辨率；
2、根据object的x，y值计算$\theta$角，通过向下取整的方式把点运数据投影到不同扇形区域内，然后每个扇形区域内的点根据半径距离也向下取整并从小到大排列；
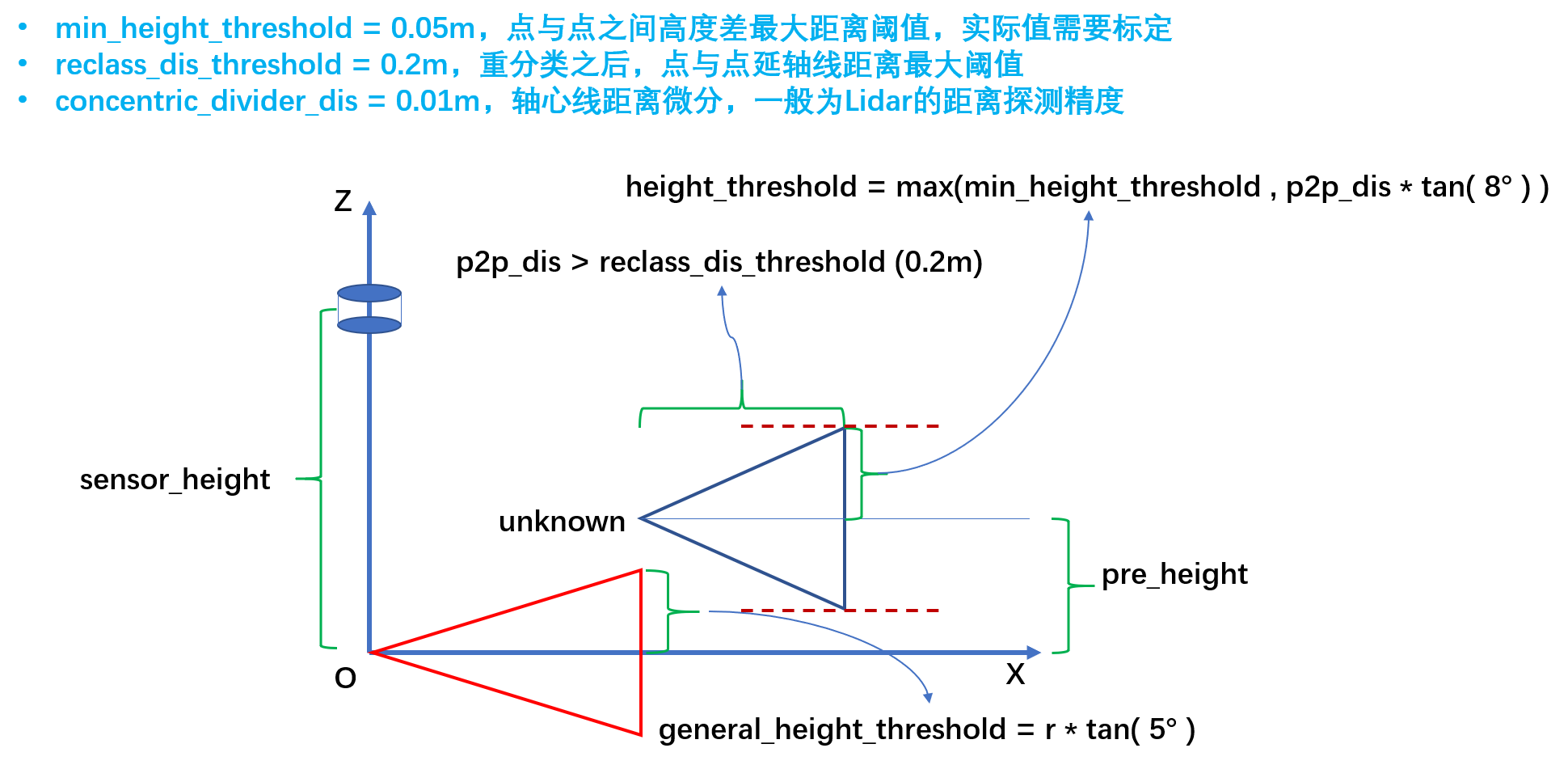
3、设置点与点之间最大坡度 point2point_max_slope = 5° 和地面坡度 ground_max_slope = 8°，根据实际情况标定；
4、计算点与点之间的高度阈值 point_height_threshold 和 ground_height_threshold 以及 point_distance；

计算开始之前，需要将原有点云数据转类型，新类型除包含原有数据内容，还添加了投影在xy平面的半径，X轴方向上的夹角$\theta$，扇形分割的序列索引，所在扇形根据半径从小到大重排列的序列索引，以及原始点云序列索引

struct PointXYZRTCO
{pcl::PointXYZ point; 	// 保存原始点云数据 float radius;		 	// cylindric coords on XY Planefloat theta;		 	// angle deg on XY planesize_t radial_div;   	// index = 保存点云数据属于哪个扇形size_t concentric_div;  // index = 保存该扇形点云的重排列序列size_t original_index;  // index = 保存原始点云序列
};

对LIDAR的扫描区域进行扇形分割，每个扇形区域的点云将组成一条射线

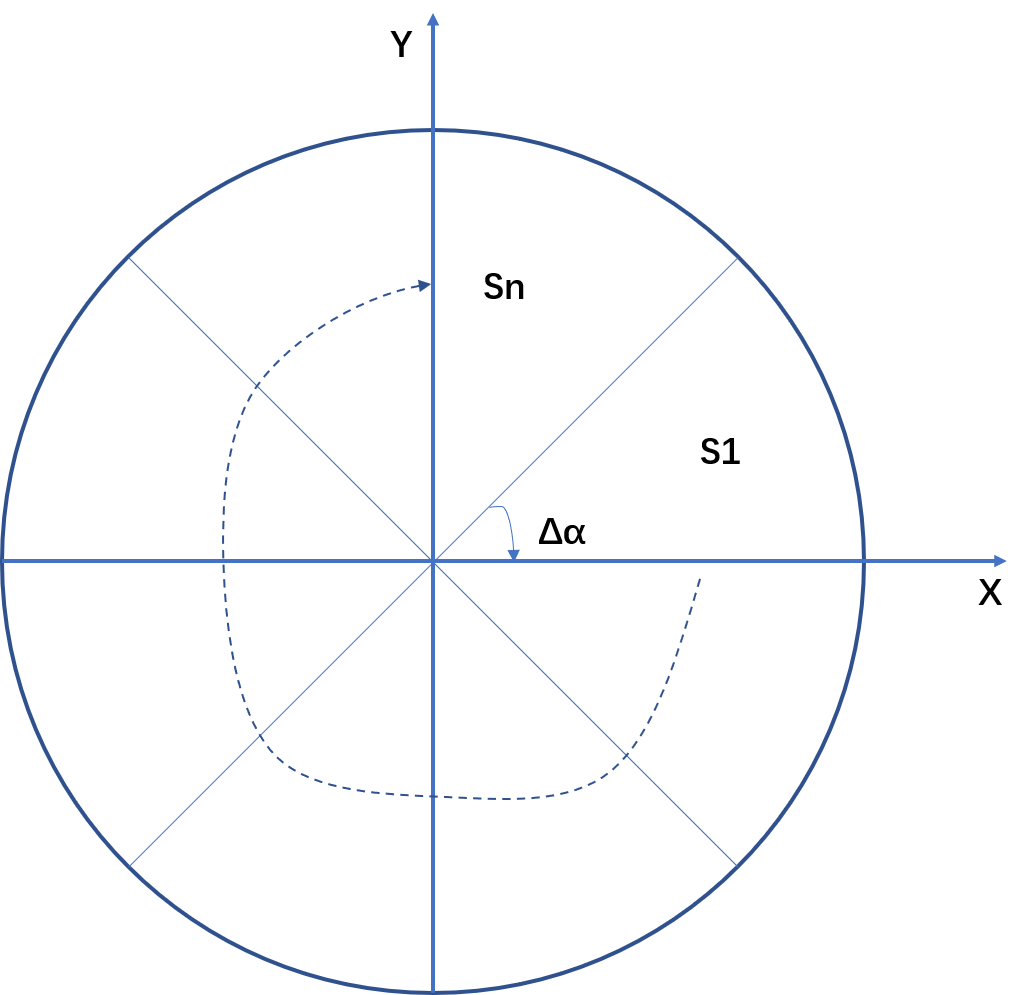
对扇形区域内的点云，进行重排列：
1、根据 floor($\theta$ / 0.18°），对点云的射线所以归属进行取值；
2、然后，根据每个点云数据的x，y坐标值计算每个点云所在圆弧的半径r，根据半径r，将原有射线上的点云进行从小到大的顺序排列；

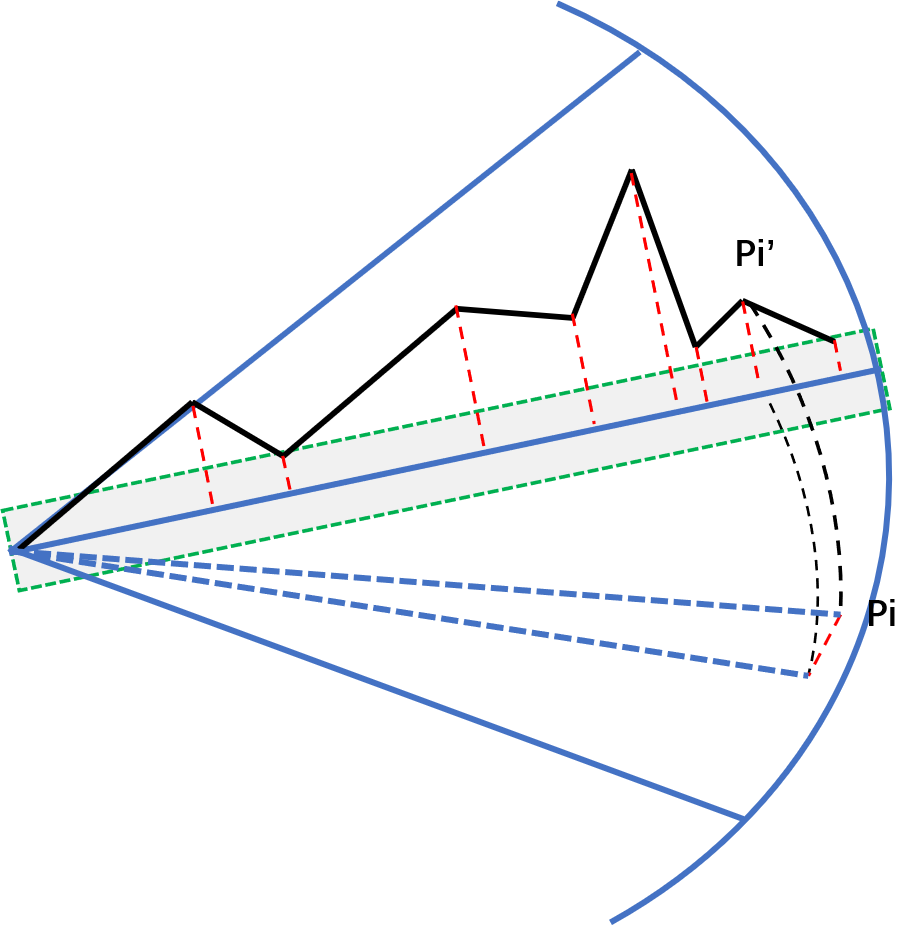
根据每条射线的点云分布，对其进行地面分割：
1、首先，对点与点之间坡度以及地面总体坡度进行估计，该估计值属于经验值，对于不同雷达，在分割数据时，需要进行标定调参；
2、从射线的最小端开始，计算点与点之间之间的距离，和高度差的阈值；

当前点高度属于前一个点高度 ± 点与点高度阈值情况，即
current_point.z ∈ (pre_point.z - height_threshold , pre_point.z + height_threshold) ：
1、情况一，前个点属于非地面的情况：

• 如果，当前点的高度也属于负的Lidar高度 ± 地面高度通用阈值，即current_point.z ∈ (- sensor_height - general_height_threshold , - sensor_height + general_height_threshold) ：得到当前点为地面点；
• 否则，也属于非地面点。

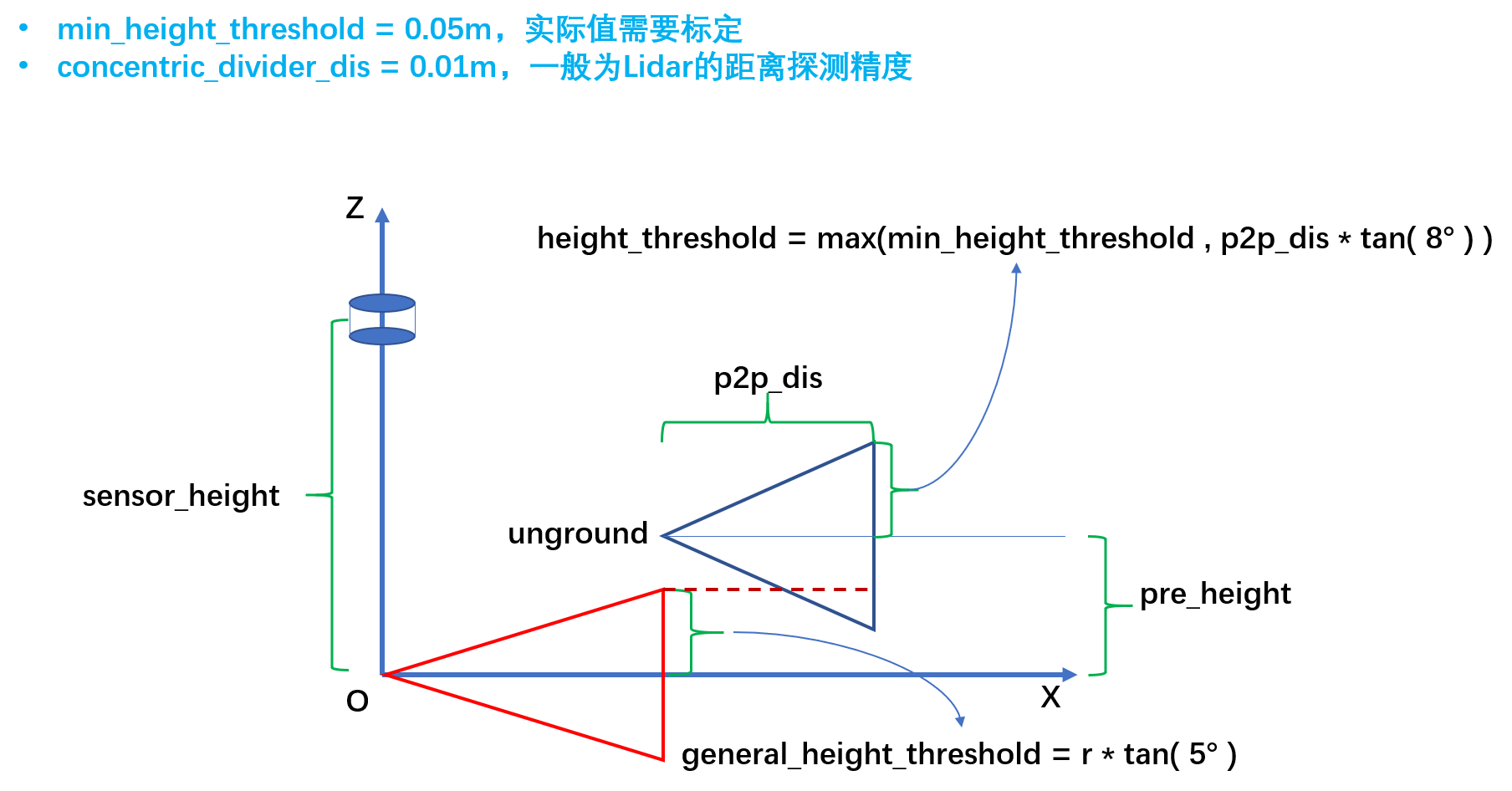
当前点高度属于前一个点高度 ± 高度阈值情况，即
current_point.z ∈ (pre_point.z - height_threshold , pre_point.z + height_threshold) ：
2、情况二，前个点属于地面的情况：

• 此时，当前点也为地面点。

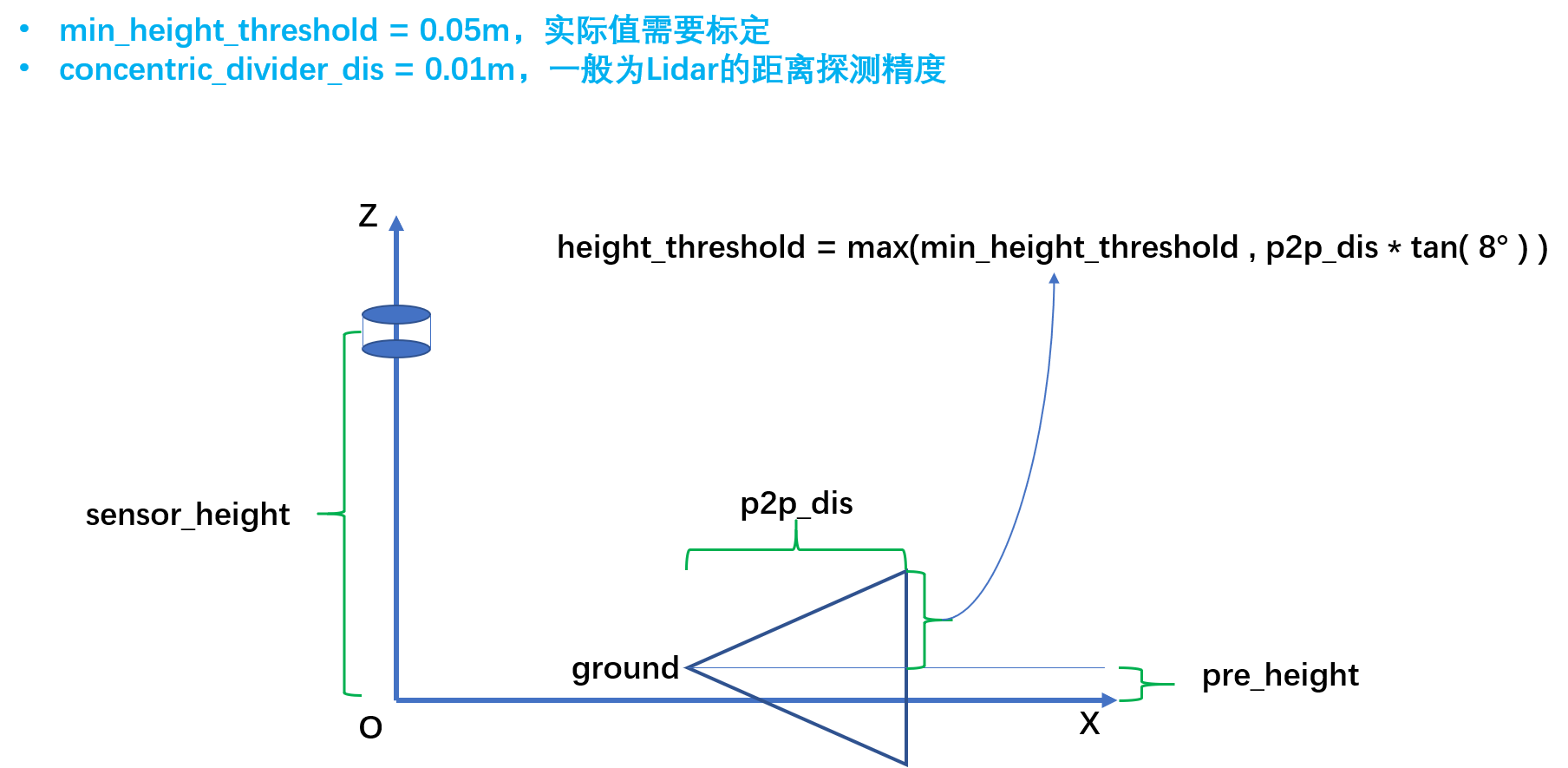
当前点高度不属于前一个点高度 ± 高度阈值情况，即
current_point.z ∉ (pre_point.z - height_threshold , pre_point.z + height_threshold) ：
1、情况一，当前点的高度属于负的Lidar高度 ± 地面高度通用阈值，即current_point.z ∈ (- sensor_height - general_height_threshold , - sensor_height + general_height_threshold) && 点与点之间的距离很大p2p_distance > reclass_distance_threshold：得到当前点为地面点；
2、其他情况，当前点都为非地面点。

分割后，地面点云：

分割后，非地面点云：

目标聚类

本工程基于非地面分割点云数据进行欧式聚类

1. PCL库 欧式聚类
2. 深度学习 Point++ / PointNet++ / PointRCNN
3. Fast and Furious: Real Time End-to-End 3D Detection, Tracking and Motion Forecasting with a Single Convolutional Net (1) (2) (3) (4)

对于2/3的方式，下一步可以尝试优化3D检测跟踪

欧式聚类

PCL库使用kd-tree加快欧式聚类算法进度

Kd-tree详解：(1)
欧式聚类算法流程详解： (1) (2)
由于点云数据在距离增加的时候，离散度在不断增加，所以考虑这种情况，在下面传参的时候根据距离判断传入不同的容忍度：

std::vector<pcl::PointIndices> local_indices;
pcl::EuclideanClusterExtraction<PointT> euclid;
euclid.setInputCloud(in_ground_cloud_2d);
euclid.setClusterTolerance(in_max_cluster_distance[i]);
euclid.setMinClusterSize(50);
euclid.setMaxClusterSize(10000);
euclid.setSearchMethod(tree);
euclid.extract(local_indices);

KD-Tree 搜索过程关键点：
k = 3情况下，x，y，z三个方向的超平面选择方法，根据三个方向上数值方差最大值判断超平面选择顺序，根据均值选择二分点；
方差越大，数据分布越离散，选择最大的可以很好的将数据分割开来。

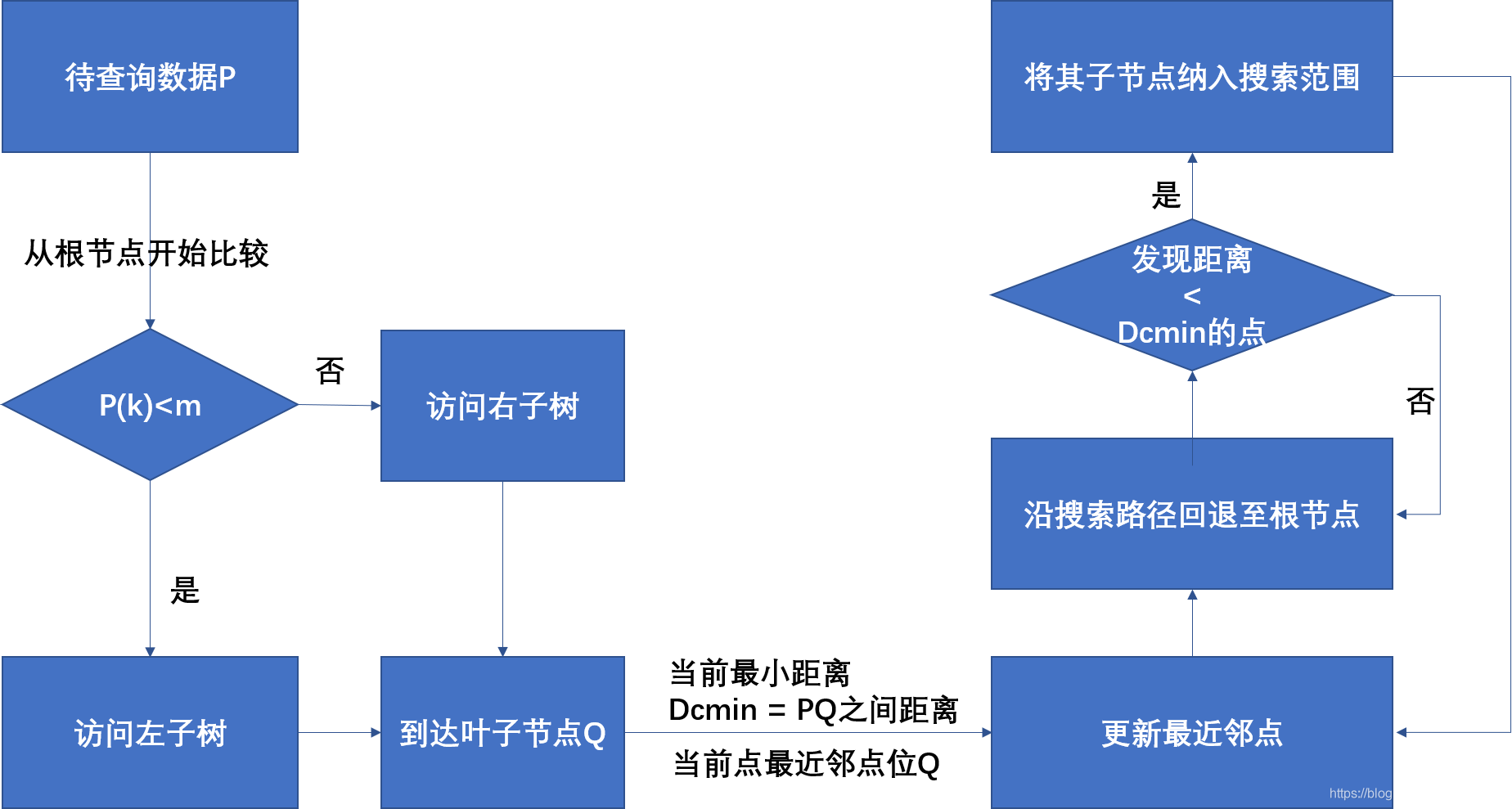
KD搜索流程，二分速度就是快：
图中对于给定的查询数据点m，须从KD-Tree的根结点开始进行比较，其中m(k)为当前结点划分维度k上数据点m对应的值，d为当前结点划分的阈值。若 m(k)小于d，则访问左子树；否则访问右子树，直至到达叶子结点Q。此时Q就是当m前最近邻点，而m与Q之间的距离就是当前最小距离Dmin 。随后沿着原搜索路径回退至根结点，若此过程中发现和m之间距离小于 Dmin的点，则须将未曾访问过的子节点均纳入搜索范畴，并及时更新最近邻点，直至所有的搜索路径都为空，整个基于KD-Tree结构的最近邻点查询过程便告完成。

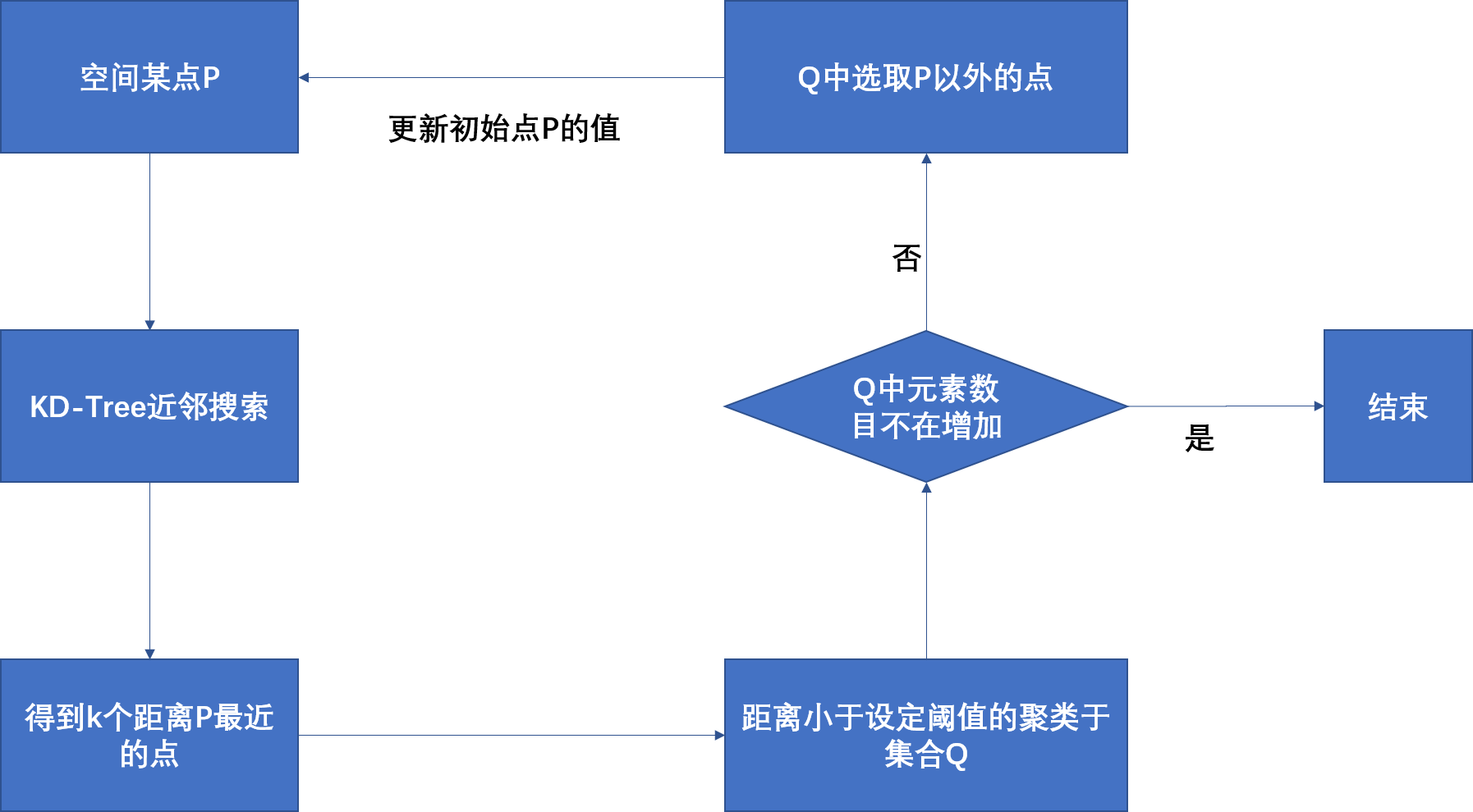
欧式聚类流程：
对于欧式聚类来说，距离判断准则为欧氏距离 $Eu=sqrt((xk-xi{)}^2+(yk-yi{)}^2+(zk-zi{)}^2+...)$。对于空间某点P，通过KD-Tree近邻搜索算法找到k个离p点最近的点，这些点中距离小于设定阈值的便聚类到集合Q中。如果Q中元素的数目不在增加（或者小于最小搜索数目，或者大于最大搜索数目），整个聚类过程便结束；否则须在集合Q中选取p点以外的点，重复上述过程，直到Q中元素的数目不在增加为止。

Add Bounding Boxes

对于Bounding Boxes的生成可以使用PCA主成分分析法生成更小的方框, 实现更高的预测结果精准性. 具体PCL实现可以查看这个链接：PCL-PCA.

目标跟踪

Doing

在使用深度学习目标检测算法（PointRCNN）后，该3D多目标追踪系统不需要使用GPU且取得了最快处理速度（214.7FPS）。
本工程尝试使用欧式聚类的方式获取bbox，然后根据该目标检测结果进行多目标跟踪。

1. 基础卡尔曼滤波 -> 根据需求可以优化为EKF（扩展卡尔曼滤波）和UKF（无损卡尔曼滤波）
2. 3D-MOT
3. A Baseline for 3D Multi-Object Tracking 原文 （译文）

基础卡尔曼滤波

用最简单的过程模型来描述目标运动——恒定速度模型

1. 同论文一样，对于检测目标object中 [$x$,$y$,$z$]^T 信息转化为 [$x$,$y$,$z$,$\theta$,$l$,$w$,$h$,$v_x$,$v_y$,$v_z$]^T
2. 然后根据卡尔曼滤波算法，预测更新
   $X_k$ = $F$ · $X_{k-1}$ + $B$ · $u_k$
   $P_k$ = $F$ · $P_{k-1}$ · $F^T$ + $Q$
   $G_k$ = $P_k$ · $C^T$ / ( $F$ · $P_k$ · $F^T$ + $R$)
   $X_k$ = $X_k$ + $G_k$ · ($Z$ - $C$ · $X_k$)
   $P_k$ = ($I$ − $G_k$ · $C$) · $P_k$
3. 其中，$X_k$ 为状态向量，$F$ 为状态转移矩阵，$B$为控制矩阵，$P_k$为估计状态概率分布的协方差矩阵， $Q$是我们的过程噪声的协方差矩阵，由于过程噪声是随机带入的，所以$u_k$ 本质是一个高斯分布：$u_k$ ~ $N$($0$,$Q$)，$Q$是过程噪声的协方差，$C$为测量矩阵，$Z$为实际测量值矩阵，同样对于恒速运动模型，我们可以将$B$ · $u_k$忽略。
4. 特别注意，过程噪声协方差矩阵获取方式参考（1），论文中用的过程噪声协方差矩阵，值为0.01的7*7方阵，并且没有考虑到采样时间问题，直接考虑时间为等值分布。

3D-IoU ( Interserction over Union)

从1D-IoU到2D-IoU推导

匈牙利算法（Hungarian）

匹配前后帧的对象，中心思想为二分图查找 实现最大匹配数

3D-MOT

中心思想就是使用每次检测结果的去估计