数据结构学习笔记之二叉排序树、平衡二叉树和最优带权二叉树
二叉树应用
- 一、二叉排序树
- 1、定义
- 2、构造
- 3、查找
- 4、插入
- 5、删除
- 7、二叉排序树的效率
- 二、平衡二叉树
- 1、定义
- 2、插入
- 2.1、LL平衡旋转
- 2.2、RR平衡旋转
- 2.3、LR平衡旋转
- 2.4、RL平衡旋转
- 3、生成
- 4、查找
- 三、最优带权二叉树
- 1、定义
- 2、哈夫曼算法
- 3、哈夫曼编码
- 主要有二叉排序树、平衡二叉树和哈夫曼树及哈夫曼编码。
一、二叉排序树
1、定义
- 二叉排序树,也称为
二叉查找树,要么为空树,要么满足下列条件:
1)若左子树非空,则左子树上的所有结点的值均小于根节点的值;
2)若右子树非空,则右子树上的所有节点的值均大于根节点的值;
3)左、右子树分别也是一棵二叉排序树。
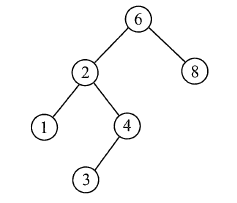
- 因此,对二叉排序树进行中序遍历可以得到一个递增序列。
2、构造
- 构造一棵二叉排序树,其算法描述如下:
void BST_Creat(BTree &T, int k[], int len) {T=NULL;int i=0;while(i<len){BST_Insert(T,str[i]);i++;} }
3、查找
二叉排序树的查找是从根节点开始,沿某个分支逐层向下比较的过程。
1)若二叉树非空,先用给定值与根节点值比较,若相等,则查找成功;
2)若不等,若小于根节点值,则在根节点左子树上查找;
3)若不等,若大于根节点值,则在根节点右子树上查找;
4)重复以上步骤,直到查找成功或遍历完所有节点返回查找失败。- 根据以上算法思想,可编辑如下二叉排序树的查找的递归函数:
BSTNode *BST_Search(BTree T, int key) {while(T!=NULL&&key!=T->data){if(key<T->data) T=T->lchild;else T=T->rchild;}return T; }
4、插入
- 二叉排序树的插入,是一个一边遍历一边比较确定插入位置的过程,其过程的主要思想如下:
1)若原二又排序树为空,则直接插入结点;
2)否则,若关键字k小于根结点值,则插入到左子树;
3)若关键字k大于根结点值,则插入到右子树。 插入的结点一定是一个新添加的叶结点,且是查找失败时的査找路径上访问的最后一个结点的左孩子或右孩子。
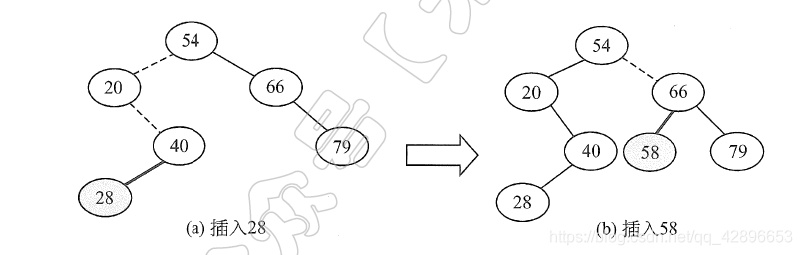
- 该过程的代码如下:
int BST_Insert(BTree &T, int k) {if(T==NULL){T = new BTree;T->key=k;T->lchild=T->rchild=NULL;return 1;}else if(k==T->key)return 0;else if(k<T->key)return BST_Insert(T->lchild,k);elsereturn BST_Insert(T->rhild, k); }
5、删除
- 二叉排序树的节点删除操作,与链表删除操作类似,都要先将要删除的节点从二叉树中摘下来,将其子树根据一定规则链接到父结点上:
1)若要删除的是叶子,则直接删除;
2)若要删除的是分支节点,且只有左子树或右子树,则直接让其子树直接成为其父结点的子树;
3)若要删除的是分支节点,且有两棵子树,则令其直接后继(或直接前驱)替代自己,然后从二叉排序树中删除这个直接后继(或直接前驱),转为前两种情况。
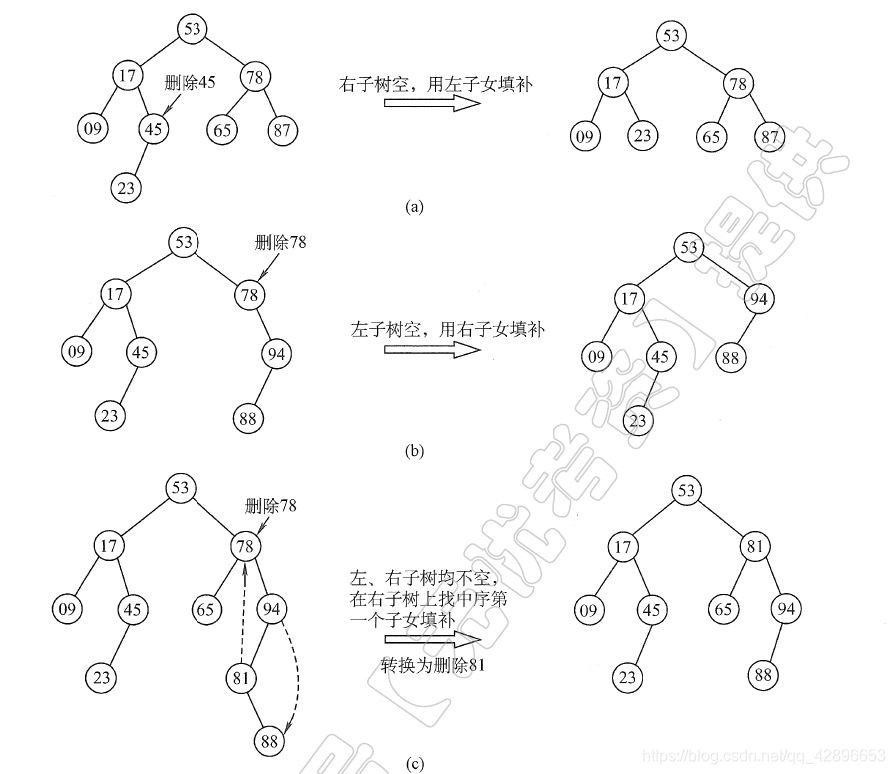
7、二叉排序树的效率
- 二叉排序树的查找效率,主要取决于树的高度。若二叉排序树的左、右子树的高度之差的绝对值不超过1,则这样的二又排序树称为平衡二叉树,它的平均查找长度为O(log2n)。若二叉排序树是一个只有右(左)孩子的单支树(类似于有序的单链表),则其平均查找长度为O(n)。
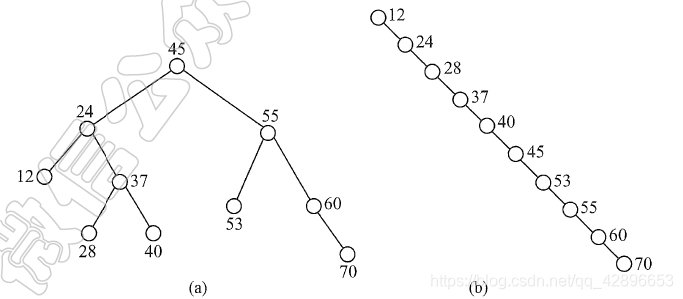
- b 是在输入有序序列产生的二叉排序树,是一种最坏情况,此种情况下查找成功的平均查找长度为:ASLb=
(1+2+3+4+5+6+7+8+9+10)/10=5.5。 - 在等概率情况下,a 树查找成功的平均长度为 ASLa=
(1+2*2+3*4+4*3)/10=2.9.(层号*层宽)。 - 从查找过程看,二叉排序树与二分査找相似。就平均时间性能而言,二又排序树上的査找和二分査找差不多。但二分査找的判定树唯一,而二义排序树的査找不唯一,相同的关键字其插入顺序不同可能生成不同的二叉排序树。
- 就维护表的有序性而言,二又排序树无须移动结点,只需修改指针即可完成插入和删除操作,平均执行时间为O(log2n)。二分査找的对象是有序顺序表,若有插入和删除结点的操作,所花的代价是O(n)。当有序表是静态査找表时,宜用顺序表作为其存储结构,而采用二分查找实现其查找操作;若有序表是动态査找表,则应选择二又排序树作为其逻辑结构。
二、平衡二叉树
1、定义
- 一棵二叉树,
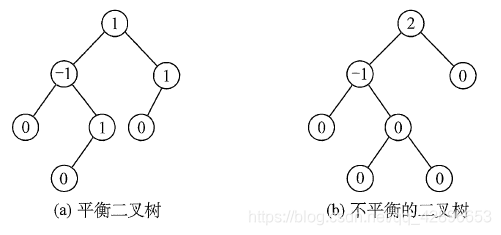
任意节点的左、右子树高度差的绝对值不超过1,则将这种二叉树称为平衡二叉树(Balanced Binary Tree),简称平衡树,并定义节点左右子树高度差为该节点的平衡因子(-1, 0, 1)。 - 将上述描述进行归纳,得出平衡二叉树的递归定义:
1)树非空,根节点的左右子树高度差绝对值不超过 1
2)根节点左子树满足平衡二叉树条件;
3)根节点右子树满足平衡二叉树条件;
2、插入
- 平衡二叉树在执行插入操作时,必须保证树的平衡性不被破坏,其基本思想如下:
1)每当插入一个节点时,首先检查其插入路径上的节点是否会因为此此操作出现不平衡;
2)若导致了不平衡,先找到插入路径上离插入节点最近的平衡因子的绝对值大于 1 的节点,再对以此节点为根的子树,在保持平衡性的前提下,调整各节点的位置关系,整体达到平衡。
- 出现不平衡进行调整的调整规律如下:
2.1、LL平衡旋转
- 又称为
右单旋转。

- 由于在结点A的左孩子(L)的左子树(L)上插入了新结点,A的平衡因子由1增至2,导致以A为根的子树失去平衡,需要一次向右的旋转操作。
将A的左孩子B向右上旋转代替A成为根结点,将A结点向右下旋转成为B的右子树的根结点,而B的原右子树则作为A结点的左子树。 - 如图所示,结点旁的数值代表结点的平衡因子,而用方块表示相应结点的子树,下方数值代表该子树的高度。
2.2、RR平衡旋转
-
又称为
左单旋转。
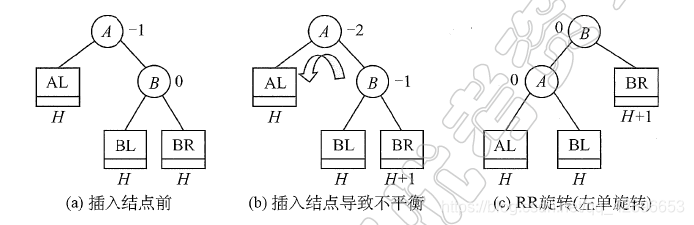
-
由于在结点4的右孩子(R)的右子树(R)上插入了新结点,A的平衡因子由-1减至-2,导致以A为根的子树失去平衡,需要一次向左的旋转操作。
将A的右孩子B向左上旋转代替A成为根结点,将A结点向左下旋转成为B的左子树的根结,而B的原左子树则作为A结点的右子树。
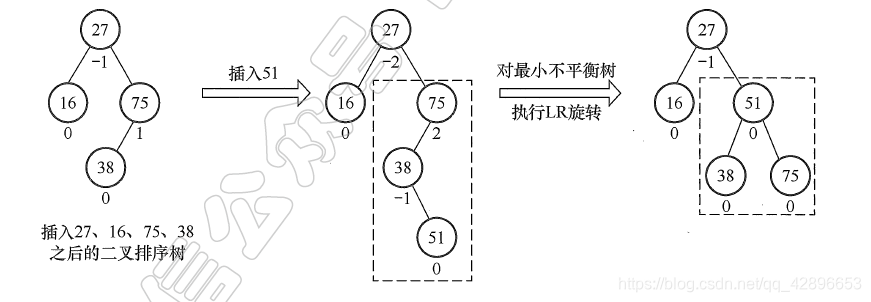
2.3、LR平衡旋转
- 又称为
先左后右双旋转。
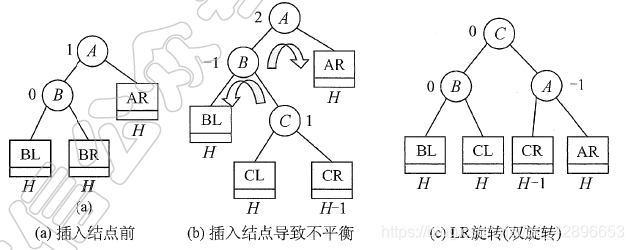
- 由于在A的左孩子(L)的右子树(R)上插入新结点,A的平衡因子由1增至2,导致以A为根的子树失去平衡,需要进行两次旋转操作,先左旋转后右旋转。
先将A结点的左孩子B的右子树的根结点C向左上旋转提升到B结点的位置,然后再把该C结点向右上旋转提升到A结点的位置。
2.4、RL平衡旋转
- 又称为
先右后左双旋转。
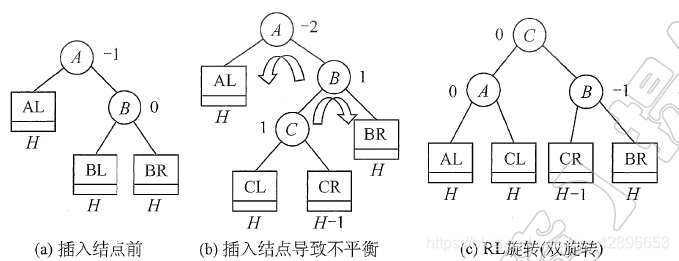
- 由于在A的右孩子(R)的左子树(L)上插入新结点,A的平衡因子由-1减至-2,导致以A为根的子树失去平衡,需要进行两次旋转操作,先右旋转后左旋转。
先将A结点的右孩子B的左子树的根结点C向右上旋转提升到B结点的位置,然后再把该C结点向左上旋转提升到A结点的位置。
3、生成
- 由关键字序列{15,3,7,10,9,8},生成一棵平衡二叉树的过程如下:
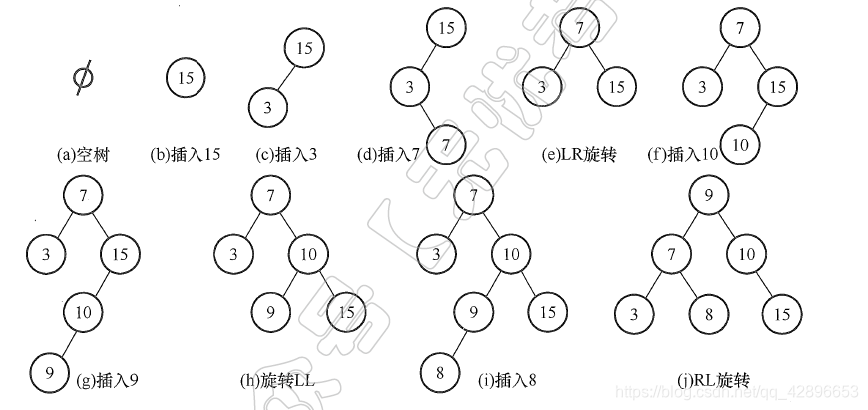
4、查找
- 在平衡二又树上进行査找的过程与二又排序树的相同。因此,在查找过程中,与给定值进行比较的关键字个数不超过树的深度。假设以mh表示深度为h的平衡树中含有的最少结点数。显然,有m0=0,m1=1,m2=2,并且有mh=mh-1+mh-2+1.可以证明,含有m个结点的平衡二又树的最大深度为O(log2m)因此平衡二叉树的平均查找长度为O(log2m),如图所示。
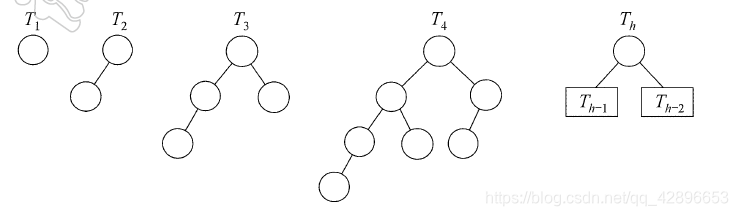
三、最优带权二叉树
1、定义
- 二叉树,在许多实际应用中,树中节点的数据域往往是具有一定意义的值,称为
权。而与此对于的,从根节点出发到任意节点路径长度与该节点权值的乘积称为带权路径长度,而所有节点的带权路径长度之后就是树的带权路径长度,即为:
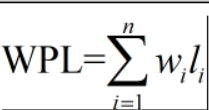
- 进一步的,
WPL最小的二叉树就是最优带权二叉树,简称最优二叉树,还叫哈夫曼树,这是因为构造最优二叉树经典算法就是哈夫曼算法。
2、哈夫曼算法
- 给定 n 个权值分别为 w1, w2, w3, … , wn 的点,根据哈夫曼算法构造最优二叉树的过程如下:
1)将这 n 个节点按从小到大的顺序排列好,视每个节点为一棵只有一个节点的二叉树,构成森林 F。
2)从 F 中选出权值最小的两棵二叉树,并将这两个二叉树分别以左右子树的形式结成一棵新的二叉树,它们的父结点的权值就是它们的权值的和。
3)将新生成的二叉树和F中剩余的二叉树重复进行上述两步骤,直到只剩下一棵二叉树。
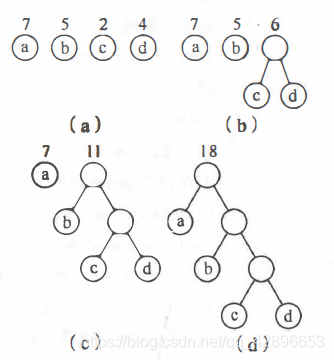
- 转为 C++ 代码描述如下:
typedef struct HTNode {int weight;int parent, lchild, rchild; }*HuffmanTree; void Select(HuffmanTree HT, int n, int &S1, int &S2) {int min1=min2=0;for(int j=1;j<=n;j++){if(HT[j].parent=0){min1=min2=HT[j].wieght;break;}}int i=1,k=1;while(i<=n){if(min1>HT[i].weight&&HT[i].parent==0){min1=HT[i].weight;S1=i;}i++;}while(k<=n&&j!=S1){if(min2>HT[k].weight&&HT[j].parent==0){min2=HT[k].weight;S2=k;}k++;} } void CreateHT(HuffmanTree &HT, int n) {if(n<=1)return;int m = 2*n-1;HT = new HTNode[m+1];for(int i=1;i<m;i++){HT[i].parent=0;HT[i].lchild=0;HT[i].rchild=0;}for(int i=1;i<=m;i++)cin>>HT[i].weight;int s1=s2=0;for(int i=n+1; i<m;++i){Select(HT, i-1, s1, s2);HT[s1].parent=i;HT[s2].parent=i;HT[i].lchild=s1;HT[i].rchild=s2;HT[i].wight=HT[s1].weight+HT[s2].weight;} }
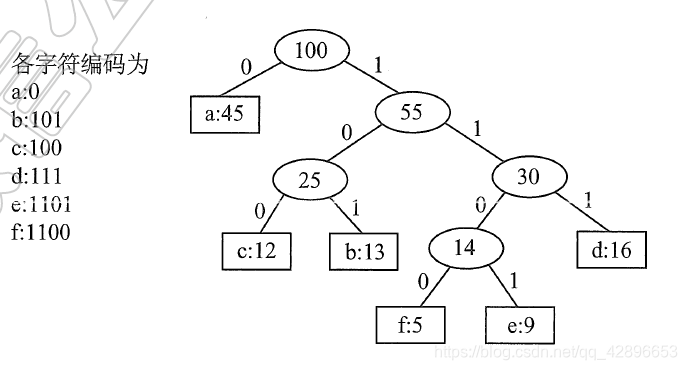
3、哈夫曼编码
- 指利用构造哈夫曼树的过程进行编码,以英文为例,每个字母出现的频率在所有英文资料中是不一样的,那么则可以根据字母出现的频率赋予每个字母适当的权值,让后便是利用哈夫曼算法对这些序列构造成一棵二叉树,然后从根节点出发左路径代表0,右路径代表1,如下图: