包括遗传算法在内的现代优化算法简介
现代优化算法是 80 年代初兴起的启发式算法。这些算法包括禁忌搜索（tabu search），模拟退火（simulated annealing），遗传算法（genetic algorithms），蚁群算法，人工神经网络（neural networks）。它们主要用于解决大量的实际应用问题。
-
模拟退火算法
来自于不同T【温度】下的粒子状态，高T高能量；低T低能量，且低T时粒子趋于稳定【热平衡】。
如果用粒子的能量定义材料在状态i 之下的能量为 E(i) ，那么材料在温度T 时从状态i 进入状 态 j 就遵循如下规律：
（1）如果 E( j) ≤ E(i) ，接受该状态被转换。
（2）如果 E( j) > E(i) ，则状态转换以如下概率被接受：
K 是物理学中的波尔兹曼常数。
在某一个特定温度T，材料达到热平衡，材料处 于状态i 的概率满足波尔兹曼分布：
x 表示材料当前状态的随机变量，S 表示状态空间集合，
此式可求两个极限：
| S | 表示集合 S 中状态的数量。这表明所有状态在高温下具有相同的概率。温度下降时：
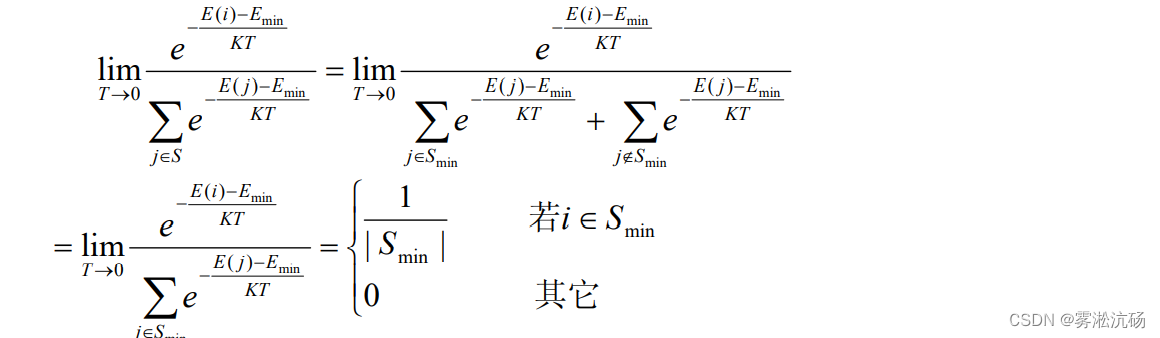
上式表明当温度降至很低时，材料会以很大概率进入最小能量状态。这个特性可用到寻找最小值的优化问题中。
初始温度T0，优化问题的一个初始解 x(0)，x(0) 生成下一个 解 x'，接受 x' 作为一个新解 x(1) 依赖于下面概率：
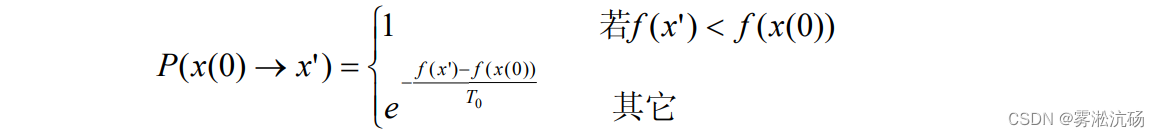
显然，更优【更小】就接受，否则以概率接受。推广到温度Ti的第K个解也是按照上式的：
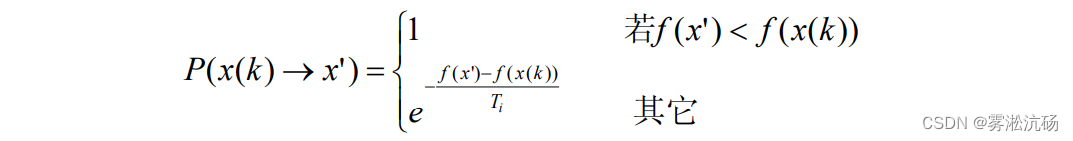
降低温度Ti ，得到Ti+1 < Ti 。在Ti+1 下重复上述 过程。因此整个优化过程就是不断寻找新解和缓慢降温的交替过程。最终的解是对该问题寻优的结果。
这个过程依赖于前一个过程，而与前前个过程乃至更前的过程无关，因此这是一个马尔可夫过程。分析后表明一个事实：
从任何一个状态 x(k) 生成 x' 的 概率，在 N(x(k)) 中是均匀分布的，且新状态 x' 被接受的概率满足上式。
经过有限次的转换，在温度Ti下的平衡态xi 的分布由下式给出：
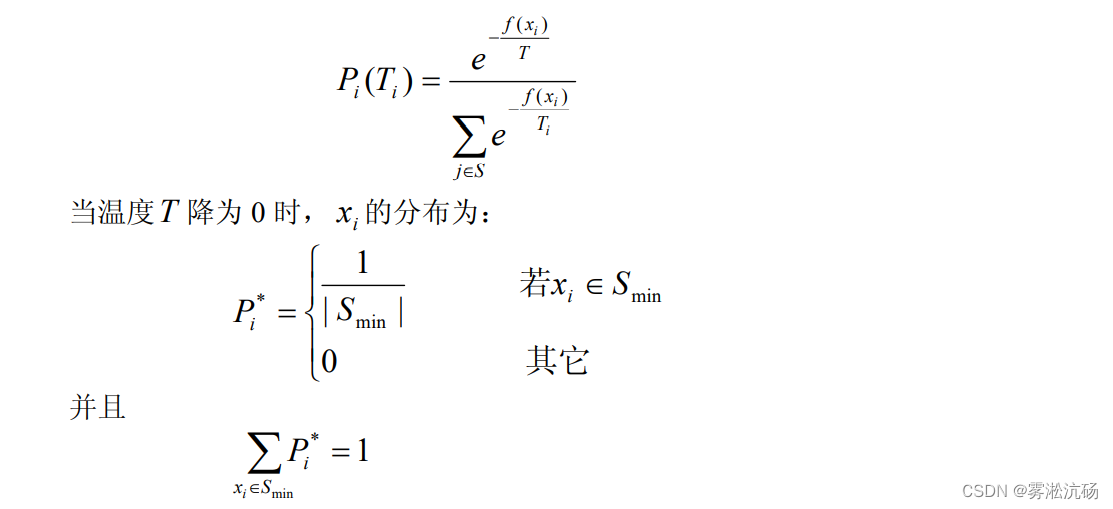
这说明，如果温度下降缓慢，则能够达到热平衡，则全局最优解将被以概率1被找到。
最终温度的确定可以提前定 为一个较小的值Te ，或连续几个温度下转换过程没有使状态发生变化算法就结束。
模拟退火算法实例——飞机侦察n个点【最后回到原来位置】最短路径问题
有100个目标需要侦察，设它们的标号为2-101，自己原来的位置为1，最后回到原来位置，设标号为102。
这里建立坐标系，转化经纬度为两个点之间的距离暂d且不说。着重描述算法求解步骤：
1.解空间
解空间 S 可表为{1,2,……,101,102 }的所有固定起点和终点的循环排列集合，
初始解可选为(1,2……,102)，
2.目标函数
此时的目标函数为侦察所有目标的路径长度或称代价函数。
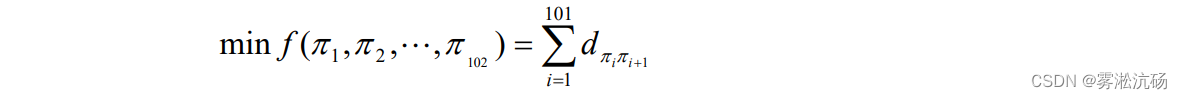
3.新解的产生
有交换一个序列的两点和选一个点插到某处两种办法，产生新的序列
4.代价函数差
对于交换两点变换法，路径差可表示为：
5.接受准则
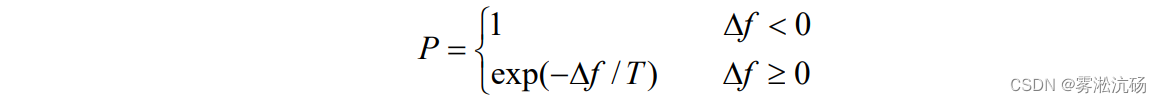
如果Δf < 0 ，则接受新的路径。否则，以概率exp(−Δf /T) 接受新的路径，即若 exp(−Δf /T) 大于 0 到 1 之间的随机数则接受。
6.降温
利用选定的降温系数α 进行降温即：T =αT，得到新的温度，这里我们取 α = 0.999。
7.结束条件
用选定的终止温度e=10的-30次方，判断退火过程是否结束。若T < e ，算法结束，输出当前状态。
-
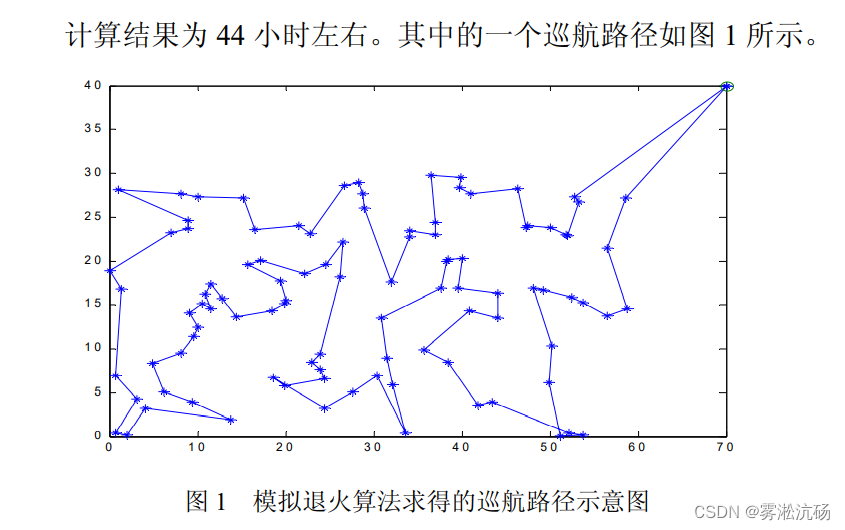
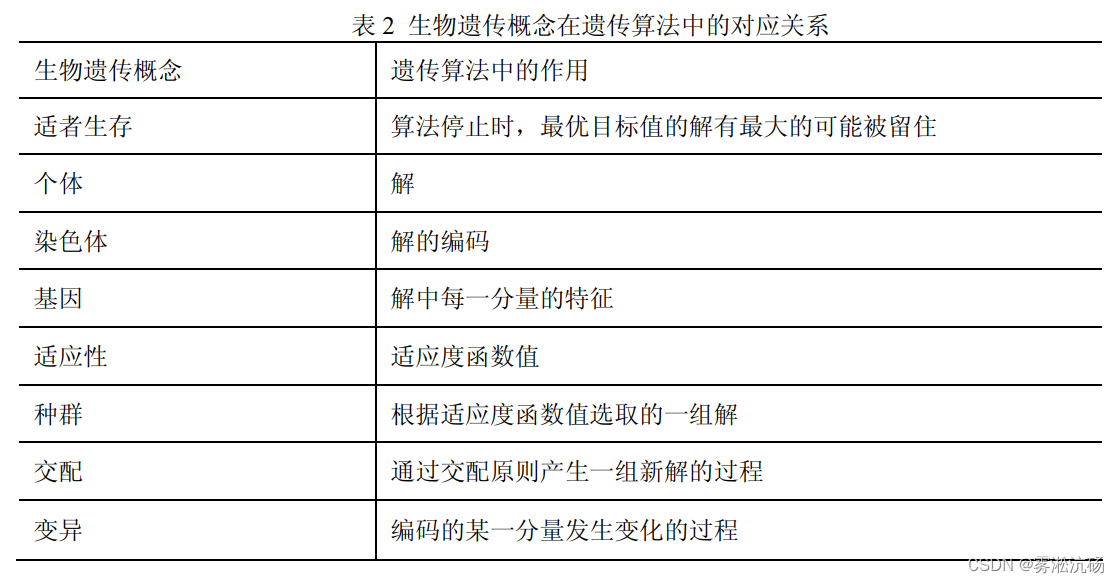
遗传算法
一种基于自然选择原理和自然遗传机制的搜索（寻优）算法。
群体搜索技术，适者生存，最优解或准最优解
实现方法：
- 用数值串或字符串表示 可行解域的每一解。
- 适应度函数度量好坏。
- 确定进化参数群体规模 M【一般来说，每一代群体的个体数目都取相等。群体规模越大、越容 易找到最优解。】 、交叉概率 pc 、变异概率 pm 、进化终止条件【可以设定到某一代进 化结束，也可以根据找出近似最优是否满足精度要求来确定。】。
遗传算法步骤：
1.编码策略【设置初始种群】
用随机数列 ω1 ω2……作为染色体；每一个随机序列都和种群中的一个个体相对。
2.目标函数
目标函数为侦察所有目标的路径长度，适应度函数就取为目标函数。
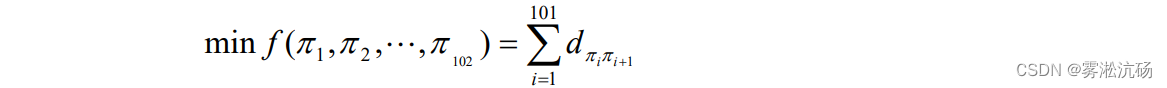
3.交叉操作
单点交叉，随机地选取第 t 个基因处为交叉点。随机交叉两个父代。
交叉方式许多，选取好的交叉方式，能保证子代能继承父代的优良特性
4.变异操作
按照给定的变异率，对选定变异的个体，随机地取三个整数，满足1 < u < v < w<..... ， 把u,v 之间（包括u 和v ）的基因段插到 w 后面。
5.选择
采用确定性的选择策略，例如贪心算法。选择目标函数值最小的 M 个个体进化到下一代， 这样可以保证父代的优良特性被保存下来。
-
蚁群算法
蚁群总是能够发 现从蚁巢到食物源的最短路径，因为：
激素进行信息交流，趋向于走激素积累较多的路径
找到最 短路径的蚂蚁总是最早返回巢穴，从而在路上留下了较多的激素
正反馈选择，到最后所有的蚂蚁都会趋向于选择这条最短路径
蚁群算法具有群体合作，正反馈选择，并行 计算等三大特点，并且可以根据需要为人工蚁加入前瞻、回溯等自然蚁所没有的特点。
步骤：
生成具有一定数量蚂蚁的蚁群。
每只人工蚁从问题的初始状态出发，根据“激素”浓度来选择下一个要转移到的状态，直到建立起一个解。
根据所找到的解的好坏程度，在所经过的状态上释放与解的质量成正比例的“激素”。
之后，每只蚂蚁又开始新的求解过程，直到寻找到满意解。
为避免停滞现象，引入了激素更新机制。
详细公式描述：
- 设人工蚁群在并行地搜索 TSP 的解，并通过激素相互通信。
- 在时刻t 人工蚁 k 由位置i 转移至位置 j 的转移概率为：
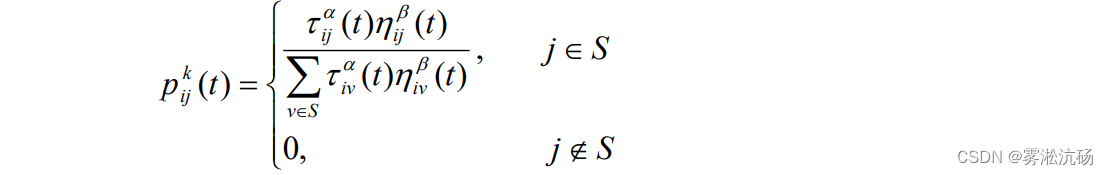
参数α 为轨迹的相对重要性（α ≥ 0 ）；β 为能见度的相对重要性（ β ≥ 0 ）；S 为 可行点集，即蚂蚁 k 下一步允许选择的城市。α, β 分别反映了蚂蚁在运动过程中所积 累的信息及启发式因子在蚂蚁选择路径中所起的不同作用。
3.当 m 个人工蚁按上式找到了可行解，则将各边的信息量用下式修改【留下多少激素量的计算方程】：
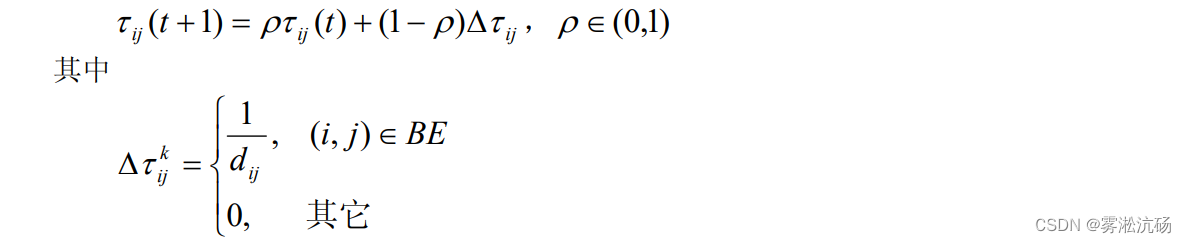
为第 k 只蚂蚁在本次循环中留在路径(i, j) 上的激素量； 
为本次循环中路径(i, j) 上的信息量的增量；参数 ρ 为轨迹的持久性；1− ρ 为轨迹衰减度，表示激素息消逝程度。
为两城市i 和 j 之间距离。BE 为本次最优路线上的边集。