当前位置：首页 > article >正文

基于PCRLB的CMIMO雷达网络多目标跟踪资源调度

article 2025/7/4 11:34:26

针对分布式组网CMIMO雷达多目标跟踪(MTT)场景，博客分析了一种目标-雷达匹配方案与功率联合优化算法。在采用分布式组网融合架构的基础上，推导包含波束和功率分配的后验克拉美罗界(PCRLB)。随后，将该效用函数结合CMIMO雷达系统资源，建立了波束分配与功率联合优化模型。最后，利用迭代优化算法进行求解，利用协方差交叉CI融合完成多部雷达对多个目标的协同跟踪，有效提高组网CMIMO雷达的综合跟踪精度。

1.目标运动模型

图1为CMIMO雷达对多个目标同时跟踪的场景示意图。

图1 CMIMO网络同时多波束跟踪

假设Q个彼此分离的目标做匀速直线CV运动，第q个目标在第k时刻的运动模型定义：

$\boldsymbol{x}_{k}^{q}=\boldsymbol{F}_{q} \boldsymbol{x}_{k-1}^{q}+\boldsymbol{u}_{k-1}^{q}$

其中 $\boldsymbol{x}_{k}^{q}=\left[x_{k}^{q}, \dot{x}_{k}^{q}, y_{k}^{q}, \dot{y}_{k}^{q}\right]^{\mathrm{T}}$ 为状态向量。

状态转移矩阵为：

$\boldsymbol{F}_{q}=\boldsymbol{I}_{2} \otimes\left[\begin{array}{ll} 1 & T \\ 0 & 1 \end{array}\right]$

$\boldsymbol{u}_{k-1}^{q}$ 为一个零均值的高斯白噪声，其协方差表示为：

$\boldsymbol{Q}_{k-1}^{q}=\boldsymbol{\kappa}_{q} \boldsymbol{I}_{2} \otimes\left[\begin{array}{ll} \frac{1}{3} T^{3} & \frac{1}{2} T^{2} \\ \frac{1}{2} T^{2} & T \end{array}\right]$

$\boldsymbol{\kappa}_{q}$ 是用来控制过程噪声大小的系数。

2.雷达量测模型

设CMIMO雷达坐标为（0, 0）。在k时刻对Q个目标进行跟踪，第q个目标对应量测和状态向量之间的转换关系表示为：

$\boldsymbol{z}_{q, k}=\boldsymbol{h}_{q, k}\left(\boldsymbol{x}_{k}^{q}\right)+\boldsymbol{v}_{q, k}$

其中 $\boldsymbol{v}_{q, k} \sim N\left(0, \boldsymbol{R}_{q, k}\right)$ 为量测噪声， $\boldsymbol{h}_{q, k}\left(\boldsymbol{.}\right)$ 为量测和状态向量之间的映射过程，分别为距离、速度与角度：

$\begin{array}{l} \boldsymbol{h}_{q, k}(\bullet)=\left[r_{q, k}(\bullet), f_{q, k}(\bullet), \varphi_{q, k}(\bullet)\right]^{\mathrm{T}} \\ \left\{\begin{array}{l} r_{q, k}\left(\boldsymbol{x}_{k}^{q}\right)=\sqrt{\left(x_{k}^{q}\right)^{2}+\left(y_{k}^{q}\right)^{2}} \\ f_{q, k}\left(\boldsymbol{x}_{k}^{q}\right)=-\frac{2}{\lambda} *\left(\dot{x}_{k}^{q}, \dot{y}_{k}^{q}\right)\binom{x_{k}^{q}}{y_{k}^{q}} / r_{q, k} \\ \varphi_{q, k}\left(\boldsymbol{x}_{k}^{q}\right)=\arctan 2\left(y_{k}^{q}\right) /\left(x_{k}^{q}\right) \end{array}\right. \end{array}$

量测噪声的协方差矩阵表示为：

$\begin{array}{l} \boldsymbol{R}_{q, k}=\operatorname{diag}\left(\boldsymbol{R}_{r_{q, k}}^{2}, \boldsymbol{R}_{f_{q, k}}^{2}, \boldsymbol{R}_{\varphi_{q k}}^{2}\right) \\ \left\{\begin{array}{l} \boldsymbol{R}_{r_{q, k}}^{2} \propto\left(\alpha_{q, k} P_{q, k}\left|\sigma_{k}^{q}\right|^{2}\right)^{-1} \\ \boldsymbol{R}_{f_{q, k}}^{2} \propto\left(\alpha_{q, k} P_{q, k}\left|\sigma_{k}^{q}\right|^{2}\right)^{-1} \\ \boldsymbol{R}_{\varphi_{q, k}}^{2} \propto\left(\alpha_{q, k} P_{q, k}\left|\sigma_{k}^{q}\right|^{2}\right)^{-1} \end{array}\right. \end{array}$

其中， $\sigma_{k}^{q}$ 为目标RCS， $P_{k,q}$ 为实际功率， $\alpha_{k,q}$ 为大小与距离4次方成反比的衰减系数。上式可以看出，在跟踪过程中，目标RCS和雷达发射参数均会影响量测协方差。

3.多目标跟踪PCRLB递推

跟踪滤波的无偏估计量与目标状态向量之间满足：

$\mathbb{E}_{x_{k}^{q}, \boldsymbol{x}_{g, k}}\left\{\left[\hat{x}_{k \mid k}^{q}\left(\boldsymbol{z}_{q, k}\right)-\boldsymbol{x}_{k}^{q}\right]\left[\hat{x}_{k \mid k}^{q}\left(z_{q, k}\right)-\boldsymbol{x}_{k}^{q}\right]^{\mathrm{T}}\right\} \geq \operatorname{FIM}^{-1}\left(\boldsymbol{x}_{k}^{q}\right)$

其中为 $\hat{x}_{k \mid k}^{q}\left(\boldsymbol{z}_{q, k}\right)$ 无偏估计量； $\mathbb{E}_{x_{k}^{q}, \boldsymbol{x}_{g, k}}$ 表示数学期望操作； ${FIM}^{-1}\left(\boldsymbol{x}_{k}^{q}\right)$ 表示PCRLB矩阵，对应逆矩阵为目标q所对应的Fisher Information Matrix。其递推公式为：

$\begin{array}{l} \operatorname{FIM}\left(\boldsymbol{x}_{k}^{q}\right)=\operatorname{FIM}_{P}\left(\boldsymbol{x}_{k}^{q}\right)+\operatorname{FIM}_{z}\left(\boldsymbol{x}_{k}^{q}\right) \\ =\left[\boldsymbol{Q}_{k-1}^{q}+\boldsymbol{F}_{q} \operatorname{FIM}^{-1}\left(\boldsymbol{x}_{k-1}^{q}\right) \boldsymbol{F}_{q}^{\mathrm{T}}\right]^{-1}+\boldsymbol{H}_{q, k}^{\mathrm{T}}\left(\hat{\boldsymbol{R}}_{q, k}\right)^{-1} \boldsymbol{H}_{q, k} \end{array}$

其中 $\operatorname{FIM}_{P}\left(\boldsymbol{x}_{k}^{q}\right)$ 表示目标状态先验分布对应的FIM， $\operatorname{FIM}_{Z}\left(\boldsymbol{x}_{k}^{q}\right)$ 为量测信息FIM。 $\boldsymbol{H}_{q, k}$ 表示雅克比矩阵： $\boldsymbol{H}_{q, k}^{\mathrm{T}}=\left[\nabla_{\chi_{k}^{g}} r_{q, k}, \nabla_{x_{k}^{g}} f_{q, k}, \nabla_{x_{k}^{g}} \varphi_{q, k}\right]$ 。对FIM求逆得到PCRLB矩阵：

$F_{P C R L B}\left(P_{k}^{q}, U_{k}^{q}, \boldsymbol{x}_{k}^{q}\right)=\operatorname{FIM}^{-1}\left(P_{k}^{q}, U_{k}^{q}, \boldsymbol{x}_{k}^{q}\right)$

其中 $P_{k}^{q}$ 为k时刻对第q个目标分配的功率资源， $U_{k}^{q}$ 为雷达与目标的匹配方案。 $F_{P C R L B}\left(P_{k}^{q}, U_{k}^{q},\boldsymbol{x}_{k}^{q}\right)$ 对角线元素对应目标状态向量的无偏估计方差下界，可将其作为代价函数： $\mathbb{F}\left(P_{k},U_{k}, \boldsymbol{x}_{k}^{q}\right)=\max \left(\sqrt{\operatorname{tr}\left\{F_{P C R L B}\left(P_{k}^{q}, U_{k}^{q}, \boldsymbol{x}_{k}^{q}\right)\right\}}\right)$ 。进一步地，可以跟踪实际物理约束构造资源调度模型，我们采用MinMax准则优化多目标跟踪精度。并利用CI融合完成多部雷达的协同跟踪。

MinMax-PCRLB优化模型可以建模为：

4.仿真实验

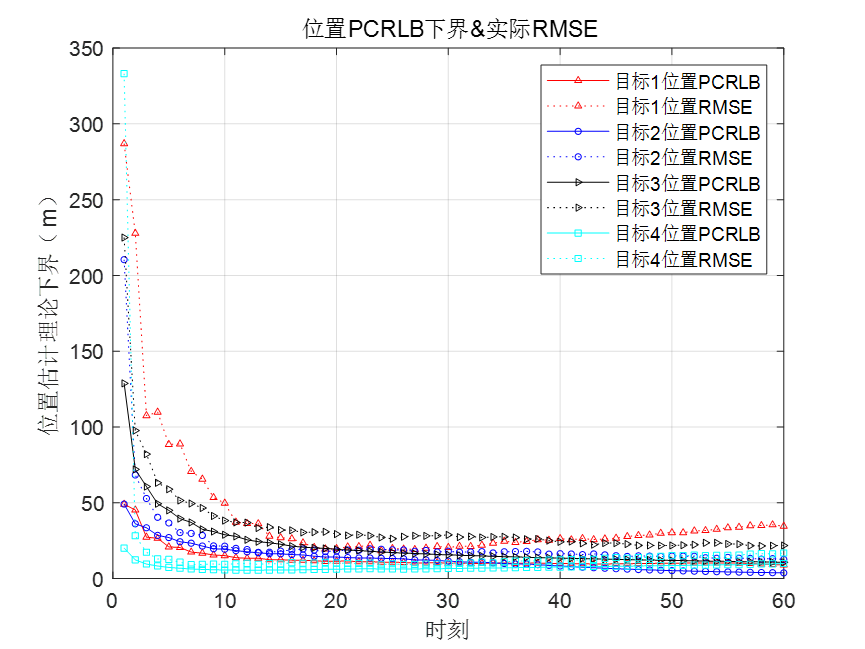
可以通过设计的优化算法进行求解，得到下一帧的雷达资源调度方案。

如有代码问题，加UltraNextYJ交流。

部分代码如下：

T = 1;                         % 采样频率
N_frame = 60;                  % 跟踪总时长
P_total = 10e3;                % 雷达总功率
RCS = 1;
lb = 0.05;                     % 功率下限
ub = 0.8;                      % 功率上限
MC = 100;                      % 蒙特卡洛次数
Bmax = 2;                      % 分配给每个目标的最多波束
Tmax = 3;                      % 每部雷达最多发射波束
Marker = 1:1:N_frame;          % 标记间隔LAMBDA = diag([1,T]);          % 用于平衡协方差矩阵中位置方差与速度方差的量纲
LAMBDA = blkdiag(LAMBDA,LAMBDA);% 初始化雷达位置
xr(:,1) = [10e3, 0, 10e3,  0]'; 
xr(:,2) = [20e3, 0, 10e3, 0]';
xr(:,3) = [30e3, 0, 10e3, 0]';
R_NUM = size(xr,2);  % 雷达个数% 初始目标状态变量【x位置，x速度，y位置，y速度】
xt(:,1) = [10e3, -120, 29e3, -90]';
xt(:,2) = [27e3, 150,  29e3, -110]';
xt(:,3) = [8e3, -120,  35e3, -90]';
xt(:,4) = [15e3, 120,  20e3,  90]';
T_NUM = size(xt,2);  % 目标个数%% 观测误差基准值
% 使用0.1P_total、全带宽、全时宽对100km处RCS为1m2的目标进行观测，基准观测误差
sigma_r_basic = 1500;
sigma_b_basic = 0.01;
sigma_v_basic = 100;
% 基准发射参数、相对位置与基准目标RCS
power_basic = 0.1 * P_total;
rcs_basic = 1;       % 基准RCS为1m2
r_basic = 50e3;      % 观测的基准距离
coef1 = sigma_r_basic^2  * power_basic * rcs_basic.^2 / (r_basic.^4);  
coef2 = sigma_b_basic^2  * power_basic * rcs_basic.^2 / (r_basic.^4);  
coef3 = sigma_v_basic^2  * power_basic * rcs_basic.^2 / (r_basic.^4); 
coef = [coef1, coef2, coef3];%% 状态转移过程构建
state_num = 4;     % 状态维度
Fk=[1, T, 0, 0; 0, 1, 0, 0; 0, 0, 1, T; 0, 0, 0, 1];   % 转移矩阵
ka = 0.2;  % 目标运动过程噪声
Qk = ka^2*[T^3/3, T^2/2,  0, 0;T^2/2, T, 0, 0; 0, 0, T^3/3, T^2/2;  0, 0, T^2/2, T];      % 过程噪声协方差
Gk= eye(4);      % 过程噪声增益矩阵% 跟踪的观测误差均值误差
v_mu = [0,0,0]';   % 观测误差的高斯白噪声的均值