数据结构*优先级队列(堆)
什么是优先级队列(堆)
优先级队列一般通过堆(Heap)这种数据结构来实现,堆是一种特殊的完全二叉树,其每个节点都满足堆的性质。如下图所示就是一个堆:

堆的存储方式
由于堆是一棵完全二叉树,所以也满足二叉树的性质:
1、 一颗非空二叉树的第i层上最多有2^(i-1)个结点。
2、 一颗深度为k的二叉树,其树的最大结点为2^k-1
3、 由第二条性质推出,具有n个结点的完全二叉树的深度k = log(n+1) [以2为底的log] 向上取整。
4、 对于任意一颗二叉树,其叶子结点为n0(结点度为0),度为2的结点个数为n2,则n0 = n2 + 1。
5、 对于具有n个结点的完全二叉树,按照从上到下、从左到右的顺序从0开始编号,则对于序号i的结点:
左孩子结点下标为2i + 1,当2i + 1 > n 时,就不存在左孩子结点。
右孩子结点下标为2i + 2,当2i + 2 > n 时,就不存在右孩子结点。
其父亲结点的下标为(i - 1) / 2。i == 0时,其结点为根节点,没有父亲结点。
当元素存入数组后,需要利用性质5来完成一些功能,完成对数组的访问。
最大堆或最小堆
对于一个完全二叉树来说:每个节点的值都大于或等于其子节点的值,堆顶元素是整个堆中的最大值,被称为最大堆;

每个节点的值都小于或等于其子节点的值,堆顶元素就是堆中的最小值,被称为最小堆。
对于最大堆或者最小堆来说,数组是最常用的实现方式。数组存储堆中的值是以层序遍历的方式来存储的。
最大堆或最小堆的创建
根据数组来创建最大堆或最小堆。以下图为例:
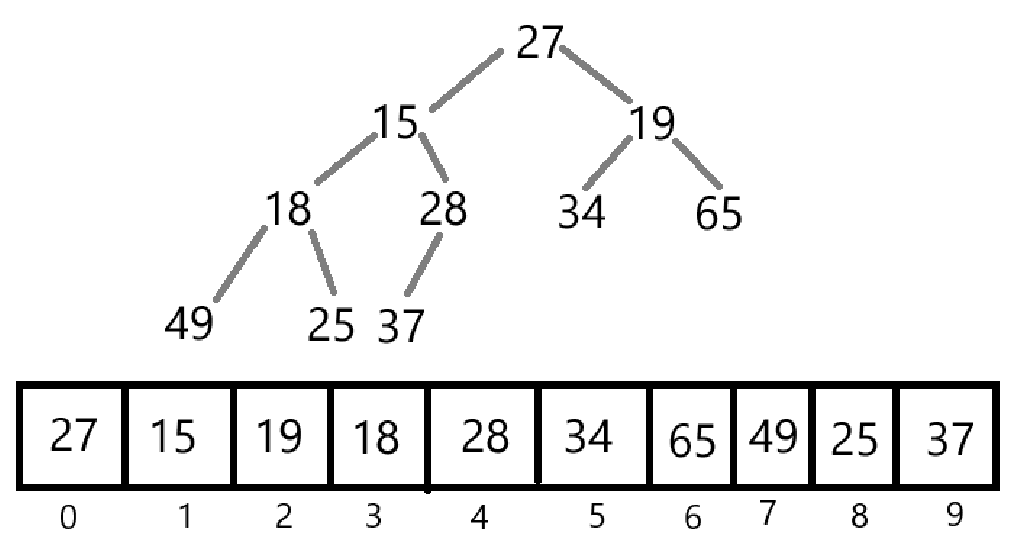
下面代码实现了最大堆
public void createHeapMAX() {//需要对每棵子树进行调整,调整方式是一样的。//parent是从最后一个孩子的父亲结点开始的,每次parent--来访问其他的树。//当parent为根节点调整完了,说明完成了最大堆的创建for (int parent = ((useSize - 1) - 1) / 2; parent >= 0; parent--) {//每个初始parent的树的向下调整siftDownMAX(parent,useSize);//传useSize的目的是为了,在parent和child交换后,parent需要到child位置在判断下一个结点是否满足最大堆,//对应的每棵树结束的标志是child下标超过useSize}
}
/*** 向下调整,让节点的值不断向下调整* @param parent* @param useSize*/
private void siftDownMAX(int parent,int useSize){//1、定义child下标int child = parent * 2 + 1;while(child < useSize) {//2、比较左右子树的值,child谁是最大值if(child + 1 < useSize && elem[child + 1] > elem[child]) {child++;}//3、判断是否交换if(elem[parent] < elem[child]) {swap(parent,child);//当前父节点变为子节点,继续检查其新的子节点(检查子树的子树)parent = child;child = parent * 2 + 1;}else {return;//如果当前父节点已经大于其子节点,那么其子树必然已经是合法的最大堆(因为构建过程是自底向上的)}}
}
private void swap(int parent,int child){int temp = elem[parent];elem[parent] = elem[child];elem[child] = temp;
}

和上述逻辑差不多,就是更改了比较符号。下面是实现最小堆的代码:
public void createHeapMIN() {for (int parent = ((useSize - 1) - 1) / 2; parent >= 0; parent--) {siftDownMIN(parent,useSize);}
}
private void siftDownMIN(int parent,int useSize){int child = parent * 2 + 1;while(child < useSize) {if(child + 1 < useSize && elem[child + 1] < elem[child]) {child++;}if(elem[parent] > elem[child]) {swap(parent,child);parent = child;child = parent * 2 + 1;}else {return;}}
}
private void swap(int parent,int child){int temp = elem[parent];elem[parent] = elem[child];elem[child] = temp;
}

上述代码的总时间复杂度为O(N)。单个siftDownMAX和siftDownMIN的时间复杂度为O(logN)
堆的删除与插入
堆的删除
在堆中删除一定是删除堆顶的元素,也就是根节点。
实现的方法是:
1、将最后一个叶子节点和根节点交换。
2、此时再删除最后一个叶子节点(原根节点)。
3、进行向下调整
public int poll() {if(isEmpty()) {return -1;}swap(0,useSize - 1);useSize--;siftDownMAX(0,useSize);return elem[0];
}
堆的插入
实现的方法是:
1、将添加的数据放在最底层。
2、在进行向上调整
public void offer(int value) {if(isFull()){elem = Arrays.copyOf(elem,2*elem.length);}elem[useSize] = value;useSize++;int child = useSize - 1;siftUp(child);
}
/*** 实现的是最大堆* @param child*/
private void siftUp(int child){int parent = (child - 1) / 2;while (child > 0) {if(elem[parent] < elem[child]) {swap(parent,child);child = parent;//向上调整parent = (child - 1) / 2;}else {break;}}
}
private void swap(int parent,int child){int temp = elem[parent];elem[parent] = elem[child];elem[child] = temp;
}上述代码的总时间复杂度为O(N*logN)。单个siftUp的时间复杂度为O(logN)。
显然较上面创建的最大堆的时间复杂度大一些。
获取堆顶元素
实现的方法是:
直接返回数组首元素即可
public int peek() {if(isEmpty()) {return -1;}return elem[0];
}
private boolean isEmpty() {return useSize == 0;
}
堆的集合类
对于堆的集合类有两种PriorityQueue 和 PriorityBlockingQueue。PriorityBlockingQueue属于线程安全的,PriorityQueue属于线程不安全的。
我们先学习PriorityQueue类
1、由于在堆的实现过程中需要进行比较,所以放置的元素一定要能比较。像对象就不能进行比较,也就不能成为元素。
2、不能传入null
3、可以任意插入多个元素,类有自动扩容的机制
public class TestPriorityQueue {public static void main(String[] args) {PriorityQueue<Student> priorityQueue = new PriorityQueue<>();PriorityQueue<Integer> priorityQueueAge = new PriorityQueue<>();Student student = new student();priorityQueueAge.offer(Student.age);//没有错误,比较的是int类型priorityQueue.offer(new Student());//会抛出ClassCastException异常priorityQueue.offer(null);//会抛出NullPointerException异常}
}
class Student {public int age;
}
构造方法
| 构造方法 | 功能 |
|---|---|
| PriorityQueue() | 创建一个空的优先级队列,初始容量为11 |
| PriorityQueue(int initialCapacity) | 初始优先级队列的容量,但不能传小于1的数字 |
| PriorityQueue(Collection<? extends E> c) | 传入一个集合类来创建堆 |
| PriorityQueue(Comparator<? super E> comparator) | 传入比较器,按照比较器的方法完成堆的排序 |
| PriorityQueue(int initialCapacity,Comparator<? super E> comparator) | 传入比较器和初始容量 |
public static void main(String[] args) {PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();priorityQueue.offer(10);priorityQueue.offer(3);priorityQueue.offer(4);System.out.println(priorityQueue.peek());//输出:3
}
//传入一个集合类
public static void main(String[] args) {ArrayList<Integer> arrayList = new ArrayList<>();arrayList.add(10);arrayList.add(3);arrayList.add(4);PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(arrayList);System.out.println(priorityQueue.peek());//输出:3
}
通过上述代码和PriorityQueue类的源码,发现,当没有传入比较器时,堆默认是按最小堆来排的。要实现最大堆就需要传入一个比较器。
1、通过实现Comparator接口(完整类),来创建一个比较器
class Compare implements Comparator<Integer> {@Overridepublic int compare(Integer o1, Integer o2) {return o2 - o1;//此时是按最大堆来建立的//return o2.compareTo(o1);//此时也是按最大堆来建立的//Integer类继承了Comparable接口//return o1 - o2;就是按最小堆来建立的}
}
public static void main(String[] args) {Compare compare = new Compare();PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(compare);priorityQueue.offer(10);priorityQueue.offer(3);priorityQueue.offer(4);System.out.println(priorityQueue.peek());//输出:10
}
2、使用匿名内部类,在需要比较器的地方直接创建匿名内部类,无需定义独立的类。
public static void main(String[] args) {PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(new Comparator<Integer>() {@Overridepublic int compare(Integer o1, Integer o2) {return o2 - o1;}});priorityQueue.offer(10);priorityQueue.offer(3);priorityQueue.offer(4);System.out.println(priorityQueue.peek());//输出:10
}
常用方法
| 方法 | 功能 |
|---|---|
| boolean offer(E e) | 添加数据 |
| E peek() | 获取堆顶的元素 |
| E poll() | 删除优先级最高的元素并返回 |
| int size() | 获取有效元素个数 |
| void clear() | 清空元素 |
| boolean isEmpty() | 判断是否为空 |
在官方中插入元素(offer())的时间复杂度为O(logN),用的是向上调整,创建堆(批量插入N个元素)的时间复杂度为O(N*logN)。使用构造方法传入集合类时,时间复杂度为O(N),用的是向下调整。
删除堆顶的元素(poll())的时间复杂度为O(logN),用的是向下调整。
关于堆的一些问题
top-K问题
代码展示:
代码一:
/*** 总时间复杂度为:O((N+k)*logN)* @param array* @param k* @return*/
public int[] topK1(int[] array,int k) {int[] ret = new int[k];if(array == null || k <= 0) {return ret;}PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(array.length);//将所有元素放到堆中,offer方法自动按照最小堆排序for (int i = 0;i < array.length;i++) {priorityQueue.offer(array[i]);}//将堆中前三个元素放到ret数组中。for (int i = 0;i < k;i++) {ret[i] = priorityQueue.poll();}return ret;
}
代码二:
/*** 总时间复杂度为:O(N*logK)* @param array* @param k* @return*/
public int[] topK(int[] array,int k) {int[] ret = new int[k];if(array == null || k <= 0) {return ret;}//根据最大根创建优先级队列PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(k, new Comparator<Integer>() {@Overridepublic int compare(Integer o1, Integer o2) {return o2 - o1;}});//创建有K个元素的堆//时间复杂度为:O(K * logK)for (int i = 0; i < k; i++) {priorityQueue.offer(array[i]);}//遍历后面的数组元素//时间复杂度为:O((N-K) * logK)for (int i = k; i < array.length; i++) {//当数组元素大于堆顶的元素,说明这个元素不是前K个最小的元素if(array[i] < priorityQueue.peek()){priorityQueue.poll();priorityQueue.offer(array[i]);}}//将堆中的前k放到ret数组中//时间复杂度为:O(K * logK) 几乎可以忽略for (int i = 0; i < k; i++) {ret[i] = priorityQueue.poll();}return ret;
}
代码解释:
对于代码一来说,是将所有元素全部放到堆中,进行堆排。如果有大量数据,会导致有很多次进行调整,时间复杂度高,为O((N+k)logN)。
对于代码二来说,只是对前K个元素进行了堆排,降低了时间复杂度,为O(NlogK)。
堆排序
如果是按照从小到大来排序,是要创建最大堆,反之创建最小堆。
以从小到大来排序为例。当创建最大堆后,将堆顶的元素和最后一个元素交换,再对剩余元
素进行调整为最大堆。重复这操作,直到整个数组有序。
这里为什么不创建最小堆呢?
当创建的是最小堆时,需要再创建一个数组,用来存放最小堆的堆顶,再对剩余元
素进行调整为最小堆。这样相比于创建最大堆,其空间复杂就会大一些。
代码展示:
/*** 从小到大排序* 时间复杂度为:O(N*logN)* 空间复杂度为:O(1)* @param array*/
public void heapSort(int[] array) {//先创建一个最大堆,时间复杂度为:O(N)for (int parent = ((array.length - 1) - 1) / 2; parent >= 0 ; parent--) {shiftDown(array,parent,array.length);}int end = array.length - 1;//进行排序,时间复杂度为:O(N*logN) <---- 有N次调整,每次调整的时间复杂度为:O(logN)while (end > 0) {swap(array,0,end);end--;shiftDown(array,0,end + 1);}
}
private void swap(int[] array,int a,int b) {int temp = array[a];array[a] = array[b];array[b] = temp;
}
private void shiftDown(int[] array ,int parent,int useSize) {int child = 2 * parent + 1;while (child < useSize) {if(child + 1 <useSize && array[child] < array[child + 1]) {child++;}if(array[parent] < array[child]) {swap(array,parent,child);parent = child;child = 2 * parent + 1;}else {break;}}
}
代码解释:

